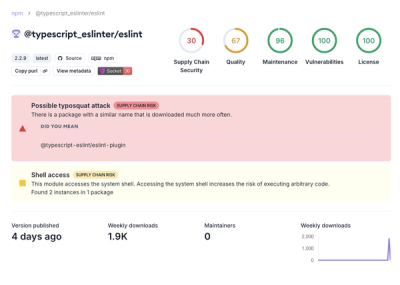
similaritymeasures
|Downloads a month| |similaritymeasures ci| |codecov| |PyPI version|
Quantify the difference between two arbitrary curves
Curves in this case are: - discretized by inidviudal data points -
ordered from a beginning to an ending
Consider the following two curves. We want to quantify how different the
Numerical curve is from the Experimental curve. Notice how there are no
concurrent Stress or Strain values in the two curves. Additionally one
curve has more data points than the other curves.
.. figure:: https://raw.githubusercontent.com/cjekel/similarity_measures/master/images/TwoCurves.png
:alt: Image of two different curves
Image of two different curves
In the ideal case the Numerical curve would match the Experimental curve
exactly. This means that the two curves would appear directly on top of
each other. Our measures of similarity would return a zero distance
between two curves that were on top of each other.
Methods covered
This library includes the following methods to quantify the difference
(or similarity) between two curves:
- Partial Curve Mapping\ x (PCM) method: Matches the area of a
subset between the two curves [1]
- Area method\ x: An algorithm for calculating the Area between two
curves in 2D space [2]
- Discrete Frechet distance\ y: The shortest distance in-between
two curves, where you are allowed to very the speed at which you
travel along each curve independently (walking dog problem) [3, 4, 5,
6, 7, 8]
- Curve Length\ x method: Assumes that the only true independent
variable of the curves is the arc-length distance along the curve
from the origin [9, 10]
- Dynamic Time Warping\ y (DTW): A non-metric distance between two
time-series curves that has been proven useful for a variety of
applications [11, 12, 13, 14, 15, 16]
- Mean absolute error\ y,z (MAE): A L1 error that requires curves
to have the same number of data points and dimensions. See
this <https://en.wikipedia.org/wiki/Mean_absolute_error>__ wiki
page. - Mean squared error\ y,z (MSE): A L2 error that requires curves to
have the same number of data points and dimensions. See
this <https://en.wikipedia.org/wiki/Mean_squared_error>__ wiki
page.
x denotes methods created specifically for material parameter
identification
y denotes that the method implemented in this library supports N-D data!
z denotes that the method requires each curve to have the same number of
data points
Installation
Install with pip
::
python -m pip install similaritymeasures
or clone and install from source.
::
git clone https://github.com/cjekel/similarity_measures
python -m pip install ./similarity_measures
Example usage
This shows you how to compute the various similarity measures
.. code:: python
import numpy as np
import similaritymeasures
import matplotlib.pyplot as plt
Generate random experimental data
x = np.random.random(100)
y = np.random.random(100)
exp_data = np.zeros((100, 2))
exp_data[:, 0] = x
exp_data[:, 1] = y
Generate random numerical data
x = np.random.random(100)
y = np.random.random(100)
num_data = np.zeros((100, 2))
num_data[:, 0] = x
num_data[:, 1] = y
quantify the difference between the two curves using PCM
pcm = similaritymeasures.pcm(exp_data, num_data)
quantify the difference between the two curves using
Discrete Frechet distance
df = similaritymeasures.frechet_dist(exp_data, num_data)
quantify the difference between the two curves using
area between two curves
area = similaritymeasures.area_between_two_curves(exp_data, num_data)
quantify the difference between the two curves using
Curve Length based similarity measure
cl = similaritymeasures.curve_length_measure(exp_data, num_data)
quantify the difference between the two curves using
Dynamic Time Warping distance
dtw, d = similaritymeasures.dtw(exp_data, num_data)
mean absolute error
mae = similaritymeasures.mae(exp_data, num_data)
mean squared error
mse = similaritymeasures.mse(exp_data, num_data)
print the results
print(pcm, df, area, cl, dtw, mae, mse)
plot the data
plt.figure()
plt.plot(exp_data[:, 0], exp_data[:, 1])
plt.plot(num_data[:, 0], num_data[:, 1])
plt.show()
If you are interested in setting up an optimization problem using these
measures, check out this Jupyter Notebook <https://github.com/cjekel/similarity_measures/blob/master/Examples_of_Similarity_Measures.ipynb>__
which replicates Section 3.2 from [2].
Changelog
Version 0.3.0: Frechet distance now supports N-D data! See
CHANGELOG.md <https://github.com/cjekel/similarity_measures/blob/master/CHANGELOG.md>__
for full details.
Documenation
Each function includes a descriptive docstring, which you can view
online here <https://jekel.me/similarity_measures/index.html>__.
References
[1] Katharina Witowski and Nielen Stander. Parameter Identification of
Hysteretic Models Using Partial Curve Mapping. 12th AIAA Aviation
Technology, Integration, and Op- erations (ATIO) Conference and 14th
AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, sep
2012. doi: doi:10.2514/6.2012-5580.
[2] Jekel, C. F., Venter, G., Venter, M. P., Stander, N., & Haftka, R.
T. (2018). Similarity measures for identifying material parameters from
hysteresis loops using inverse analysis. International Journal of
Material Forming. https://doi.org/10.1007/s12289-018-1421-8
[3] M Maurice Frechet. Sur quelques points du calcul fonctionnel.
Rendiconti del Circol Matematico di Palermo (1884-1940), 22(1):1–72,
1906.
[4] Thomas Eiter and Heikki Mannila. Computing discrete Frechet
distance. Technical report, 1994.
[5] Anne Driemel, Sariel Har-Peled, and Carola Wenk. Approximating the
Frechet Distance for Realistic Curves in Near Linear Time. Discrete &
Computational Geometry, 48(1): 94–127, 2012. ISSN 1432-0444. doi:
10.1007/s00454-012-9402-z. URL
http://dx.doi.org/10.1007/s00454-012-9402-z.
[6] K Bringmann. Why Walking the Dog Takes Time: Frechet Distance Has No
Strongly Subquadratic Algorithms Unless SETH Fails, 2014.
[7] Sean L Seyler, Avishek Kumar, M F Thorpe, and Oliver Beckstein. Path
Similarity Analysis: A Method for Quantifying Macromolecular Pathways.
PLOS Computational Biology, 11(10):1–37, 2015. doi:
10.1371/journal.pcbi.1004568. URL
https://doi.org/10.1371/journal.pcbi.1004568.
[8] Helmut Alt and Michael Godau. Computing the Frechet Distance Between
Two Polyg- onal Curves. International Journal of Computational Geometry
& Applications, 05 (01n02):75–91, 1995. doi: 10.1142/S0218195995000064.
[9] A Andrade-Campos, R De-Carvalho, and R A F Valente. Novel criteria
for determina- tion of material model parameters. International Journal
of Mechanical Sciences, 54 (1):294–305, 2012. ISSN 0020-7403. doi:
https://doi.org/10.1016/j.ijmecsci.2011.11.010. URL
http://www.sciencedirect.com/science/article/pii/S0020740311002451.
[10] J Cao and J Lin. A study on formulation of objective functions for
determin- ing material models. International Journal of Mechanical
Sciences, 50(2):193–204, 2008. ISSN 0020-7403. doi:
https://doi.org/10.1016/j.ijmecsci.2007.07.003. URL
http://www.sciencedirect.com/science/article/pii/S0020740307001178.
[11] Donald J Berndt and James Clifford. Using Dynamic Time Warping to
Find Pat- terns in Time Series. In Proceedings of the 3rd International
Conference on Knowledge Discovery and Data Mining, AAAIWS’94, pages
359–370. AAAI Press, 1994. URL
http://dl.acm.org/citation.cfm?id=3000850.3000887.
[12] François Petitjean, Alain Ketterlin, and Pierre Gançarski. A global
averaging method for dynamic time warping, with applications to
clustering. Pattern Recognition, 44 (3):678–693, 2011. ISSN 0031-3203.
doi: https://doi.org/10.1016/j.patcog.2010.09.013. URL
http://www.sciencedirect.com/science/article/pii/S003132031000453X.
[13] Toni Giorgino. Computing and Visualizing Dynamic Time Warping
Alignments in R: The dtw Package. Journal of Statistical Software; Vol
1, Issue 7 (2009), aug 2009. URL
http://dx.doi.org/10.18637/jss.v031.i07.
[14] Stan Salvador and Philip Chan. Toward Accurate Dynamic Time Warping
in Linear Time and Space. Intell. Data Anal., 11(5):561–580, oct 2007.
ISSN 1088-467X. URL http://dl.acm.org/citation.cfm?id=1367985.1367993.
[15] Paolo Tormene, Toni Giorgino, Silvana Quaglini, and Mario
Stefanelli. Matching incomplete time series with dynamic time warping:
an algorithm and an applica- tion to post-stroke rehabilitation.
Artificial Intelligence in Medicine, 45(1):11–34, 2009. ISSN 0933-3657.
doi: https://doi.org/10.1016/j.artmed.2008.11.007. URL
http://www.sciencedirect.com/science/article/pii/S0933365708001772.
[16] Senin, P., 2008. Dynamic time warping algorithm review. Information
and Computer Science Department University of Hawaii at Manoa Honolulu,
USA, 855, pp.1-23.
http://seninp.github.io/assets/pubs/senin_dtw_litreview_2008.pdf
Contributions welcome!
This is by no means a complete list of all possible similarity measures.
For instance the SciPy Hausdorff distance <https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.distance.directed_hausdorff.html>__
is an alternative similarity measure useful if you don’t know the
beginning and ending of each curve. There are many more possible
functions out there. Feel free to send PRs for other functions in
literature!
Requirements for adding new method to this library: - all methods should
be able to quantify the difference between two curves - method must
support the case where each curve may have a different number of data
points - follow the style of existing functions - reference to method
details, or descriptive docstring of the method - include test(s) for
your new method - minimum Python dependencies (try to stick to
SciPy/numpy functions if possible)
Please cite
If you’ve found this information or library helpful please cite the
following paper. You should also cite the papers of any methods that you
have used.
Jekel, C. F., Venter, G., Venter, M. P., Stander, N., & Haftka, R. T.
(2018). Similarity measures for identifying material parameters from
hysteresis loops using inverse analysis. International Journal of
Material Forming. https://doi.org/10.1007/s12289-018-1421-8
::
@article{Jekel2019,
author = {Jekel, Charles F and Venter, Gerhard and Venter, Martin P and Stander, Nielen and Haftka, Raphael T},
doi = {10.1007/s12289-018-1421-8},
issn = {1960-6214},
journal = {International Journal of Material Forming},
month = {may},
title = {{Similarity measures for identifying material parameters from hysteresis loops using inverse analysis}},
url = {https://doi.org/10.1007/s12289-018-1421-8},
year = {2019}
}
.. |Downloads a month| image:: https://img.shields.io/pypi/dm/similaritymeasures.svg
.. |similaritymeasures ci| image:: https://github.com/cjekel/similarity_measures/workflows/similaritymeasures%20ci/badge.svg
.. |codecov| image:: https://codecov.io/gh/cjekel/similarity_measures/branch/master/graph/badge.svg?token=nwuIhL8r3C
:target: https://codecov.io/gh/cjekel/similarity_measures
.. |PyPI version| image:: https://img.shields.io/pypi/v/similaritymeasures