Research
/Security News
Critical Vulnerability in NestJS Devtools: Localhost RCE via Sandbox Escape
A flawed sandbox in @nestjs/devtools-integration lets attackers run code on your machine via CSRF, leading to full Remote Code Execution (RCE).
@effect/typeclass
Advanced tools
Welcome to the documentation for @effect/typeclass, a collection of re-usable typeclasses for the Effect ecosystem.
The functional abstractions in @effect/typeclass can be broadly divided into two categories.
number and string, as well as ways of combining those values.ReadonlyArray and Option and ways of combining them.Note: members are in bold.
A type class used to name the lower limit and the upper limit of a type.
Extends:
Order| Name | Given | To |
|---|---|---|
| maxBound | A | |
| minBound | A | |
| reverse | Bounded<A> | Bounded<A> |
| clamp | A | A |
A Monoid is a Semigroup with an identity. A Monoid is a specialization of a
Semigroup, so its operation must be associative. Additionally,
x |> combine(empty) == empty |> combine(x) == x. For example, if we have Monoid<String>,
with combine as string concatenation, then empty = "".
Extends:
Semigroup| Name | Given | To |
|---|---|---|
| empty | A | |
| combineAll | Iterable<A> | A |
| reverse | Monoid<A> | Monoid<A> |
| tuple | [Monoid<A>, Monoid<B>, ...] | Monoid<[A, B, ...]> |
| struct | { a: Monoid<A>, b: Monoid<B>, ... } | Monoid<{ a: A, b: B, ... }> |
| min | Bounded<A> | Monoid<A> |
| max | Bounded<A> | Monoid<A> |
A Semigroup is any set A with an associative operation (combine):
x |> combine(y) |> combine(z) == x |> combine(y |> combine(z))
| Name | Given | To |
|---|---|---|
| combine | A, A | A |
| combineMany | A, Iterable<A> | A |
| reverse | Semigroup<A> | Semigroup<A> |
| tuple | [Semigroup<A>, Semigroup<B>, ...] | Semigroup<[A, B, ...]> |
| struct | { a: Semigroup<A>, b: Semigroup<B>, ... } | Semigroup<{ a: A, b: B, ... }> |
| min | Order<A> | Semigroup<A> |
| max | Order<A> | Semigroup<A> |
| constant | A | Semigroup<A> |
| intercalate | A, Semigroup<A> | Semigroup<A> |
| first | Semigroup<A> | |
| last | Semigroup<A> |
Parameterized Types Hierarchy
flowchart TD
Alternative --> SemiAlternative
Alternative --> Coproduct
Applicative --> Product
Coproduct --> SemiCoproduct
SemiAlternative --> Covariant
SemiAlternative --> SemiCoproduct
SemiApplicative --> SemiProduct
SemiApplicative --> Covariant
Applicative --> SemiApplicative
Chainable --> FlatMap
Chainable ---> Covariant
Monad --> FlatMap
Monad --> Pointed
Pointed --> Of
Pointed --> Covariant
Product --> SemiProduct
Product --> Of
SemiProduct --> Invariant
Covariant --> Invariant
SemiCoproduct --> Invariant
Note: members are in bold.
Extends:
SemiAlternativeCoproductExtends:
SemiApplicativeProduct| Name | Given | To |
|---|---|---|
| liftMonoid | Monoid<A> | Monoid<F<A>> |
A type class of types which give rise to two independent, covariant functors.
| Name | Given | To |
|---|---|---|
| bimap | F<E1, A>, E1 => E2, A => B | F<E2, B> |
| mapLeft | F<E1, A>, E1 => E2 | F<E2, A> |
| map | F<A>, A => B | F<B> |
Extends:
FlatMapCovariant| Name | Given | To |
|---|---|---|
| tap | F<A>, A => F<B> | F<A> |
| andThenDiscard | F<A>, F<B> | F<A> |
| bind | F<A>, name: string, A => F<B> | F<A & { [name]: B }> |
Contravariant functors.
Extends:
Invariant| Name | Given | To |
|---|---|---|
| contramap | F<A>, B => A | F<B> |
| contramapComposition | F<G<A>>, A => B | F<G<B>> |
| imap | contramap | imap |
Coproduct is a universal monoid which operates on kinds.
This type class is useful when its type parameter F<_> has a
structure that can be combined for any particular type, and which
also has a "zero" representation. Thus, Coproduct is like a Monoid
for kinds (i.e. parametrized types).
A Coproduct<F> can produce a Monoid<F<A>> for any type A.
Here's how to distinguish Monoid and Coproduct:
Monoid<A> allows A values to be combined, and also means there
is an "empty" A value that functions as an identity.
Coproduct<F> allows two F<A> values to be combined, for any A. It
also means that for any A, there is an "zero" F<A> value. The
combination operation and zero value just depend on the
structure of F, but not on the structure of A.
Extends:
SemiCoproduct| Name | Given | To |
|---|---|---|
| zero | F<A> | |
| coproductAll | Iterable<F<A>> | F<A> |
| getMonoid | Monoid<F<A>> |
Covariant functors.
Extends:
Invariant| Name | Given | To |
|---|---|---|
| map | F<A>, A => B | F<B> |
| mapComposition | F<G<A>>, A => B | F<G<B>> |
| imap | map | imap |
| flap | A, F<A => B> | F<B> |
| as | F<A>, B | F<B> |
| asUnit | F<A> | F<void> |
Filterable<F> allows you to map and filter out elements simultaneously.
| Name | Given | To |
|---|---|---|
| partitionMap | F<A>, A => Either<B, C> | [F<B>, F<C>] |
| filterMap | F<A>, A => Option<B> | F<B> |
| compact | F<Option<A>> | F<A> |
| separate | F<Either<A, B>> | [F<A>, F<B>] |
| filter | F<A>, A => boolean | F<A> |
| partition | F<A>, A => boolean | [F<A>, F<A>] |
| partitionMapComposition | F<G<A>>, A => Either<B, C> | [F<G<B>>, F<G<C>>] |
| filterMapComposition | F<G<A>>, A => Option<B> | F<G<B>> |
| Name | Given | To |
|---|---|---|
| flatMap | F<A>, A => F<B> | F<B> |
| flatten | F<F<A>> | F<A> |
| andThen | F<A>, F<B> | F<B> |
| composeKleisliArrow | A => F<B>, B => F<C> | A => F<C> |
Data structures that can be folded to a summary value.
In the case of a collection (such as ReadonlyArray), these
methods will fold together (combine) the values contained in the
collection to produce a single result. Most collection types have
reduce methods, which will usually be used by the associated
Foldable<F> instance.
| Name | Given | To |
|---|---|---|
| reduce | F<A>, B, (B, A) => B | B |
| reduceComposition | F<G<A>>, B, (B, A) => B | B |
| reduceRight | F<A>, B, (B, A) => B | B |
| foldMap | F<A>, Monoid<M>, A => M | M |
| toReadonlyArray | F<A> | ReadonlyArray<A> |
| toReadonlyArrayWith | F<A>, A => B | ReadonlyArray<B> |
| reduceKind | Monad<G>, F<A>, B, (B, A) => G<B> | G<B> |
| reduceRightKind | Monad<G>, F<A>, B, (B, A) => G<B> | G<B> |
| foldMapKind | Coproduct<G>, F<A>, (A) => G<B> | G<B> |
Invariant functors.
| Name | Given | To |
|---|---|---|
| imap | F<A>, A => B, B => A | F<B> |
| imapComposition | F<G<A>>, A => B, B => A | F<G<B>> |
| bindTo | F<A>, name: string | F<{ [name]: A }> |
| tupled | F<A> | F<[A]> |
Allows composition of dependent effectful functions.
Extends:
FlatMapPointed| Name | Given | To |
|---|---|---|
| of | A | F<A> |
| ofComposition | A | F<G<A>> |
| unit | F<void> | |
| Do | F<{}> |
Extends:
CovariantOfExtends:
SemiProductOf| Name | Given | To |
|---|---|---|
| productAll | Iterable<F<A>> | F<ReadonlyArray<A>> |
| tuple | [F<A>, F<B>, ...] | F<[A, B, ...]> |
| struct | { a: F<A>, b: F<B>, ... } | F<{ a: A, b: B, ... }> |
Extends:
SemiCoproductCovariantExtends:
SemiProductCovariant| Name | Given | To |
|---|---|---|
| liftSemigroup | Semigroup<A> | Semigroup<F<A>> |
| ap | F<A => B>, F<A> | F<B> |
| andThenDiscard | F<A>, F<B> | F<A> |
| andThen | F<A>, F<B> | F<B> |
| lift2 | (A, B) => C | (F<A>, F<B>) => F<C> |
| lift3 | (A, B, C) => D | (F<A>, F<B>, F<C>) => F<D> |
SemiCoproduct is a universal semigroup which operates on kinds.
This type class is useful when its type parameter F<_> has a
structure that can be combined for any particular type. Thus,
SemiCoproduct is like a Semigroup for kinds (i.e. parametrized
types).
A SemiCoproduct<F> can produce a Semigroup<F<A>> for any type A.
Here's how to distinguish Semigroup and SemiCoproduct:
Semigroup<A> allows two A values to be combined.
SemiCoproduct<F> allows two F<A> values to be combined, for any A.
The combination operation just depends on the structure of F,
but not the structure of A.
Extends:
Invariant| Name | Given | To |
|---|---|---|
| coproduct | F<A>, F<B> | F<A | B> |
| coproductMany | Iterable<F<A>> | F<A> |
| getSemigroup | Semigroup<F<A>> | |
| coproductEither | F<A>, F<B> | F<Either<A, B>> |
Extends:
Invariant| Name | Given | To |
|---|---|---|
| product | F<A>, F<B> | F<[A, B]> |
| productMany | F<A>, Iterable<F<A>> | F<[A, ...ReadonlyArray<A>]> |
| productComposition | F<G<A>>, F<G<B>> | F<G<[A, B]>> |
| productManyComposition | F<G<A>>, Iterable<F<G<A>>> | F<G<[A, ...ReadonlyArray<A>]>> |
| nonEmptyTuple | [F<A>, F<B>, ...] | F<[A, B, ...]> |
| nonEmptyStruct | { a: F<A>, b: F<B>, ... } | F<{ a: A, b: B, ... }> |
| andThenBind | F<A>, name: string, F<B> | F<A & { [name]: B }> |
| productFlatten | F<A>, F<B> | F<[...A, B]> |
Traversal over a structure with an effect.
| Name | Given | To |
|---|---|---|
| traverse | Applicative<F>, T<A>, A => F<B> | F<T<B>> |
| traverseComposition | Applicative<F>, T<G<A>>, A => F<B> | F<T<G<B>>> |
| sequence | Applicative<F>, T<F<A>> | F<T<A>> |
| traverseTap | Applicative<F>, T<A>, A => F<B> | F<T<A>> |
TraversableFilterable, also known as Witherable, represents list-like structures
that can essentially have a traverse and a filter applied as a single
combined operation (traverseFilter).
| Name | Given | To |
|---|---|---|
| traversePartitionMap | Applicative<F>, T<A>, A => F<Either<B, C>> | F<[T<B>, T<C>]> |
| traverseFilterMap | Applicative<F>, T<A>, A => F<Option<B>> | F<T<B>> |
| traverseFilter | Applicative<F>, T<A>, A => F<boolean> | F<T<A>> |
| traversePartition | Applicative<F>, T<A>, A => F<boolean> | F<[T<A>, T<A>]> |
Adapted from:
FAQs
A collection of reusable typeclasses for the Effect ecosystem
The npm package @effect/typeclass receives a total of 27,313 weekly downloads. As such, @effect/typeclass popularity was classified as popular.
We found that @effect/typeclass demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 3 open source maintainers collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Research
/Security News
A flawed sandbox in @nestjs/devtools-integration lets attackers run code on your machine via CSRF, leading to full Remote Code Execution (RCE).
Product
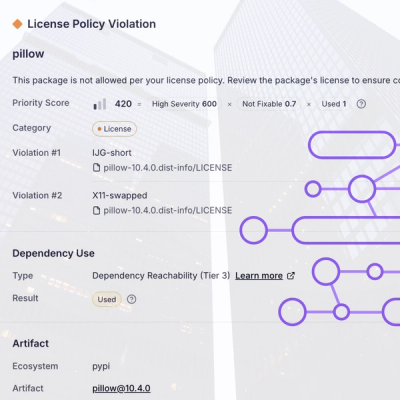
Customize license detection with Socket’s new license overlays: gain control, reduce noise, and handle edge cases with precision.

Product
Socket now supports Rust and Cargo, offering package search for all users and experimental SBOM generation for enterprise projects.