Research
/Security News
Critical Vulnerability in NestJS Devtools: Localhost RCE via Sandbox Escape
A flawed sandbox in @nestjs/devtools-integration lets attackers run code on your machine via CSRF, leading to full Remote Code Execution (RCE).
trace-ray-js
Advanced tools
A simple CPU-based ray tracer written in **vanilla JavaScript**, rendering directly to an HTML5 `<canvas>` element — no WebGL, no external libraries.
A simple CPU-based ray tracer written in vanilla JavaScript, rendering directly to an HTML5 <canvas> element — no WebGL, no external libraries.


Performance Benchmarks:
Resolutions Tested: 200x200 to 1280x720
Data: 882 spheres in a 3D Grid
Processor: 12th Gen Intel(R) Core(TM) i5-1235U 1.30 GHz
Threads: 12
Responsible for creating, updating, and destroying the canvas element used for rendering.
Core ray tracing logic:
Contains vector algebra and geometry utilities used by the ray tracer, such as:
The main HTML file that bootstraps the app and mounts the canvas.
Styling for the web interface.
Main JavaScript entry point:
To run the raytracer locally:
index.html in any modern browser
Based on origin:
Based on mathematical modeling:

To compute how a matte surface reflects light:
Reflected Intensity = Light Intensity x (I/A) = Light Intensity × cos(a)
To compute how I/A is same as cos(a) from the diagram:
This models how light spreads over a larger area at shallow angles, thus reducing its intensity.

To compute how a shiny surface reflects light:
No surface is perfectly smooth — meaning light isn't only reflected in the exact direction of R, but also slightly around it. This gives rise to specular highlights, which appear brighter when:
We calculate the reflected light intensity as follows:
Reflected Intensity = Light Intensity × (cos(a))^specular
specular exponent determines how shiny the surface is.
When a = 0 degrees (perfect alignment), the intensity is maximum.
As a increases toward 90 degrees, intensity drops rapidly.
Raising cos(a) to a high power compresses the reflection into a narrow beam — simulating a shiny surface.
During ray tracing, if the ray vector does not intersect with anything, then { r: 0, g: 0, b: 0 } is returned.
If the ray intersects with something, then depending on the intensity of light reflected by the surface, its color is modified like:
{ r: valueR * ReflectedLightIntensity, g: valueG * ReflectedLightIntensity, b: valueB * ReflectedLightIntensity }
Therefore, when no lights are present, it will be pitch black as shown in below video:
To make surfaces look shiny or mirror-like, we simulate how light bounces off them. When a ray of light hits a reflective object, we send another ray in the direction it would bounce — just like how you'd see your reflection in a mirror.
This new ray continues the same process: it might hit something else, reflect again, and so on. We recursively repeat this bounce a few times to create realistic reflections, but stop after a set limit to avoid infinite loop (like mirror infront of mirror scenario)
Limitation Right now, all of this happens on the main thread — and since every pixel may involve multiple recursive rays, the UI can freeze. Using Web Workers to offload this heavy computation can make rendering much smoother and faster.
CanvasRenderingContext2D🔄 Next Up
FAQs
A simple CPU-based ray tracer written in **vanilla JavaScript**, rendering directly to an HTML5 `<canvas>` element — no WebGL, no external libraries.
The npm package trace-ray-js receives a total of 0 weekly downloads. As such, trace-ray-js popularity was classified as not popular.
We found that trace-ray-js demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Research
/Security News
A flawed sandbox in @nestjs/devtools-integration lets attackers run code on your machine via CSRF, leading to full Remote Code Execution (RCE).
Product
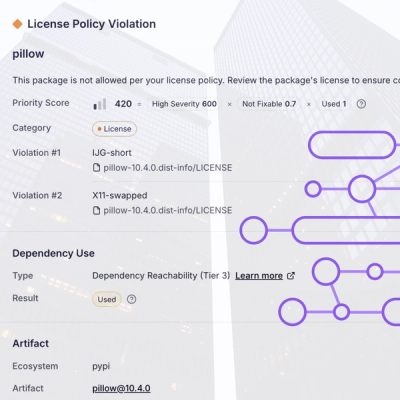
Customize license detection with Socket’s new license overlays: gain control, reduce noise, and handle edge cases with precision.

Product
Socket now supports Rust and Cargo, offering package search for all users and experimental SBOM generation for enterprise projects.