dheapy

dheapy

dheapy is a pure Python implementation of $d$-ary heap data structure for priority queue applications, which can work for both max-heap and min-heap variants. The factor $d$ in $d$-ary heap is called the branching factor and it can be equal to or greater than $2$, where $d=2$ means the heap is built with a binary tree, $d=3$ with a ternary tree, $d=4$ with a quaternary tree, and so on.

The branching factor of a tree is the maximum number of children a node can have.

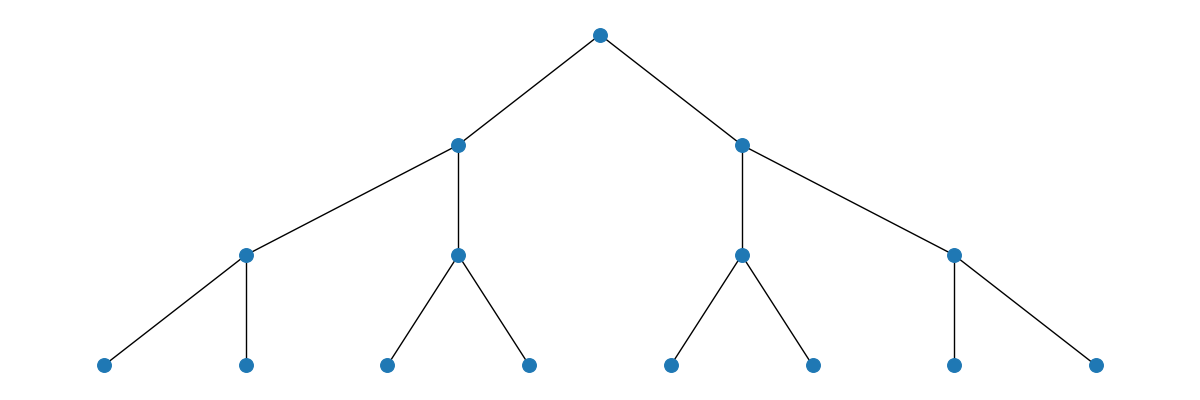
A $2$-ary heap or binary heap has a branching factor of $2$:

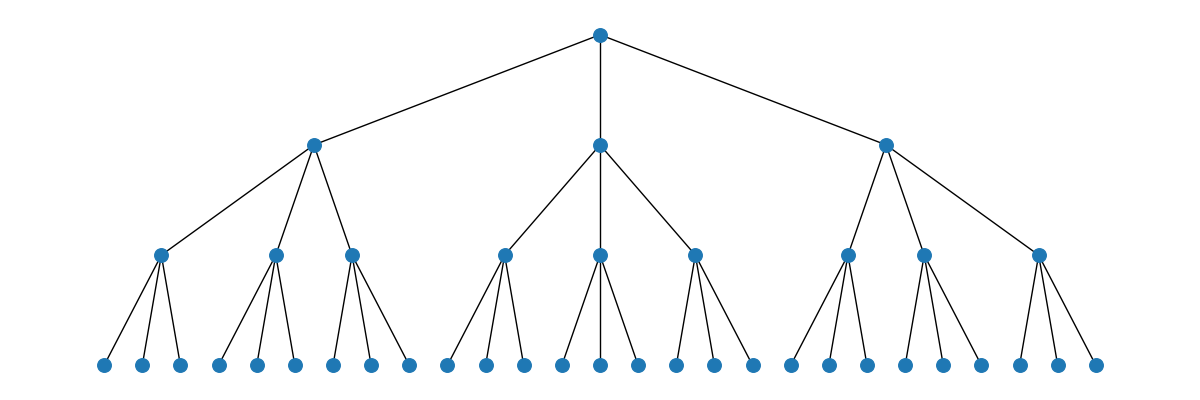
A $3$-ary heap or ternary heap has a branching factor of $3$:

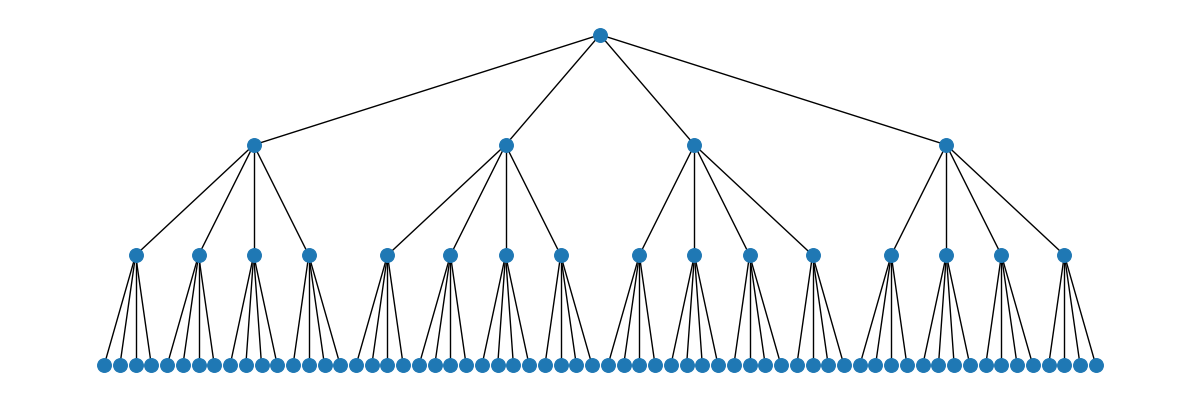
A $4$-ary heap or quaternary heap has a branching factor of $4$:

dheapy is array-based and adaptable, where arbitrary items can be removed, updated, and displayed on the go.

The library also comes with a sorting function that is based on the heap-sort algorithm to sort lists of tuples.

Installation

Use the package manager pip to install dheapy:

pip install dheapy

Prerequisites

None.

Usage

• DHeap(branching_factor=2, variant='max')
  Class to create an empty and perform priority queue operations (shown in the table below). Parameters:

  • branching_factor: int; default = 2
  • variant: str, either 'max' or 'min'; default = 'max'

  To import DHeap class:

  from dheapy import DHeap
  

• heapsorted(object, branching_factor=2, variant='max') Function for sorting arrays that is based on the heap sort algorithm. Parameters:

  • object: array or iterable
  • branching_factor: int; default = 2
  • variant: str, either 'max' or 'min'; default = 'max'

  To import heapsorted() function

  from dheapy import heapsorted
  

To create an empty priority queue with branching factor 3 and min-heap variant:

P = DHeap(3, 'min')

The following are operations that can be performed with DHeap class:

Operation	Description	Object Returned
P.insert(k,v)	adds a new item with priority number k and element/description v into priority queue. The priority number k must be positive and can be of integer or floating-point type; the priority element/description v can be of any type.
P.peek()	returns the highest priority item, but without extracting/removing it from the queue.	(k, v)
P.delete()	removes/deletes the highest priority item from the queue.	(k, v)
P.removeitem(k, v)	removes an item with priority number k and element v from the queue.	(k, v)
P.update(old_item, new_item)	updates a pair of old item (in tuple, which consists of a priority number and its element) and replaces it with a pair of new item (in tuple, which consists of a priority number and its element). This operation can also be used to update a priority number or element only.
len(P)	returns the number of items in priority queue P.	int
is_empty(P)	returns True if priority queue P does not contain any items.	True or False
P.contains(k, v)	returns True if priority queue P contains an item with priority number k with element v.	True or False
P.show(i)	returns the item at index i.	(k, v)

Performance

Operation	Time Complexity
P.insert(k,v)	O(log n)
P.peek()	O(1)
P.delete()	O(log n)
P.removeitem(k, v)	O(log n)
P.update(old_item, new_item)	O(log n)
len(P)	O(1)
is_empty(P)	O(1)
P.contains(k, v)	O(1)
P.show(i)	O(1)
function heapsorted()	O(n log n)

Example for DHeap class

• Data to be inserted in to a priority queue must be a tuple of size $2$, where the first entry must contain priority numbers (either integer or floating-point type) and the second entry can be any object. Aside from individual insertion, a group of individual items of data can also be inserted into a priority queue. Let's do an example. Prepare data to be inserted into a priority queue in a list of tuples:

toInsert = [(10, 'CGK'), (9, 'BSL'), (9.2, 'IST'), (8, 'AMS'),
            (7, 'BCN'), (5, 'DOH'), (3, 'BOS'), (8.7, 'AUH')]

• Import DHeap class:

from dheapy import DHeap

• Instantiate an empty priority queue object:

branching_factor = 3
variant = 'min'

P = DHeap(branching_factor, variant)

• To verify if parameters are correct, we print the object we just created

print(P)

which will result in

Priority Queue with 3 branching factor and min-heap

• Check if the priority queue is empty:

print(f'Is Priority Queue empty: {P.is_empty()}')
print(f'Priority Queue length = {len(P)}')

which will result in

Is Priority Queue empty: True
Priority Queue length = 0

• Insert the data into our empty priority queue P:

for i in toInsert:
    P.insert(i[0], i[1])

• Check again whether the priority queue is already filled with data and its length:

print(f'Is Priority Queue empty: {P.is_empty()}')
print(f'Priority Queue length = {len(P)}')

which will print

Is Priority Queue empty: False
Priority Queue length = 8

• Use peek() module to display the highest priority item:

print(f'Highest priority: {P.peek()}')

we'll get

Highest priority: (3, 'BOS')

Our ternary min-heap will look like as follows:

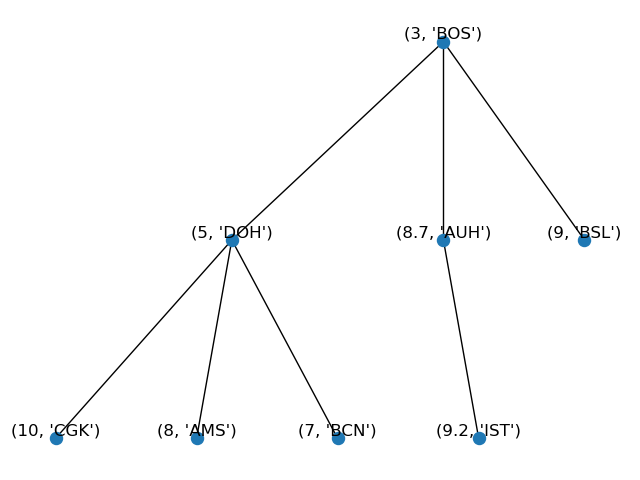
Our data will be stored in a list in an arrangement such that it starts from the root node (3, 'BOS'). The root's children will be stored subsequently, starting from the most left child (5, 'DOH') traversing horizontally through all children until the most right child (9, 'BSL'). Thus data in the list will be stored as [(3, 'BOS'), (5, 'DOH'), (8.7, 'AUH'), (9, 'BSL')]. Then children of the most left child (5, 'DOH') will be stored next, followed with children of (8.7, 'AUH'), and so on. This can be verified by using the show(i) module where i is an index number of the item position. For example, to obtain item at index $0$ or the root node, by either directly displaying like:

print(P.show(0))

with result

(3, 'BOS')

Or, to get the pair of priority number and its element individually:

priority, element = P.show(0)

then display:

print(priority, element)

Since in this example we use a ternary heap, to display all three children of the root node directly:

print(P.show(1))
print(P.show(2))
print(P.show(3))

which will give us

(5, 'DOH')
(8.7, 'AUH')
(9, 'BSL')

• Use module delete() to delete the current highest priority:

P.delete()

or to display the deleted item:

print(f'Deleted: {P.delete()}')

which will return

Deleted: (3, 'BOS')

• View the new highest priority:

print(f'Highest priority: {P.peek()}')

to get:

Highest priority: (5, 'DOH')

and our structure now will look like:

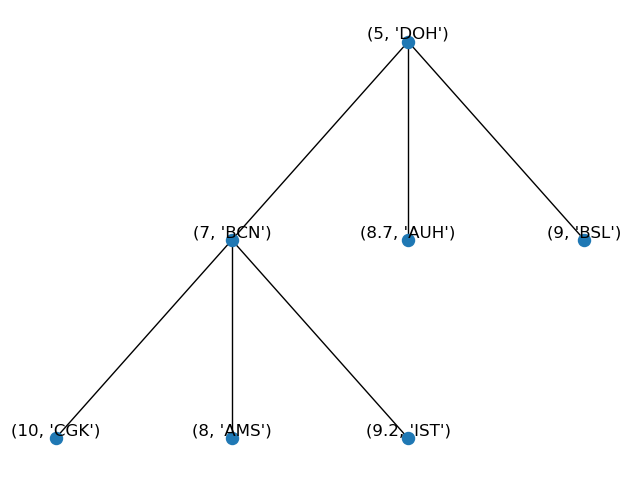
• Use removeitem(k, v) to remove an item from our priority queue, where k is a key or priority number and v is its element. For example, to remove (8.7, 'AUH'):

rm = P.removeitem(8.7, 'AUH')
print(f"Removed: {rm}")

we get

Removed: (8.7, 'AUH')

Our structure now will look like:

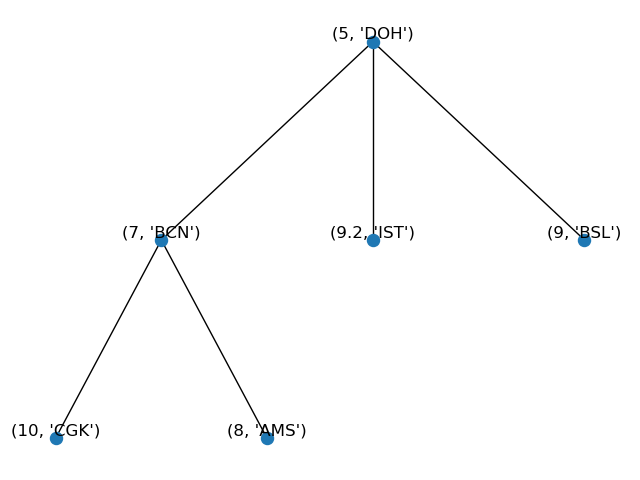
• To replace an item with a new one, use the update() module. For example, to replace the item (8, AMS) with (3.3, 'SFO'):

old_item = (8, 'AMS')
new_item = (3.3, 'SFO')
P.update(old_item, new_item)

and check the latest highest priority:

print(f'Highest priority: {P.peek()}')

will return

Highest priority: (3.3, 'SFO')

Our structure now will look like:

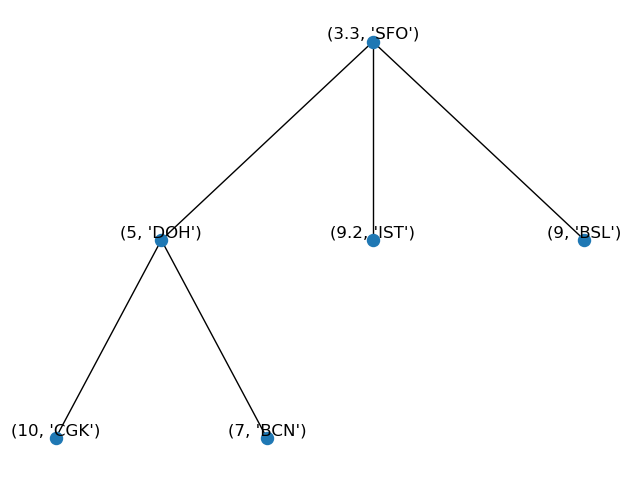
• Finally, to check if an item is in our priority queue, we can use the module contains(k, v) with k is the key or priority number of the item and v is its element:

P.contains(4.5, 'TKO')

will return

False

or

P.contains(9, 'BSL')

will return

True

Example for heapsorted function

Import the function:

from dheapy import heapsorted

The heapsorted() function is used to sort a list of tuples, just like the example data for DHeap class above.

• To sort a list of tuples data:

data = [(10, 'CGK'), (9, 'BSL'), (9.2, 'IST'), (8, 'AMS'),
        (7, 'BCN'), (5, 'DOH'), (3, 'BOS'), (8.7, 'AUH')]

branching_factor = 3
variant = 'min'
result = heapsorted(data, branching_factor, variant)

To print the result:

print(result)

we get

[(3, 'BOS'), (5, 'DOH'), (7, 'BCN'), (8, 'AMS'), (8.7, 'AUH'), (9, 'BSL'), (9.2, 'IST'), (10, 'CGK')]

• To sort data in a priority queue, we must transform the data into an array. Let's sort the priority queue P we have created in the above example. First we create an empty array, and then append the items in P into the array using the module show():

array = []

for i in range(len(P)):
    array.append(P.show(i))

Then we use the array for our function input argument:

result = heapsorted(array, branching_factor, variant)

printing the result, we'll get

[(3.3, 'SFO'), (5, 'DOH'), (7, 'BCN'), (9, 'BSL'), (9.2, 'IST'), (10, 'CGK')]

References