
Security News
Crates.io Users Targeted by Phishing Emails
The Rust Security Response WG is warning of phishing emails from rustfoundation.dev targeting crates.io users.
Smoothing via robust locally-weighted regression in one or two dimensions
.. image:: https://img.shields.io/pypi/v/loess.svg :target: https://pypi.org/project/loess/ .. image:: https://img.shields.io/badge/arXiv-1208.3523-orange.svg :target: https://arxiv.org/abs/1208.3523 .. image:: https://img.shields.io/badge/DOI-10.1093/mnras/stt644-green.svg :target: https://doi.org/10.1093/mnras/stt644
LOESS is the Python implementation by Cappellari et al. (2013) <https://ui.adsabs.harvard.edu/abs/2013MNRAS.432.1862C>_ of the
algorithm by Cleveland (1979) <https://doi.org/10.2307/2286407>_
for the one-dimensional case and Cleveland & Devlin (1988) <https://doi.org/10.2307/2289282>_ for the two-dimensional case.
.. contents:: :depth: 2
If you use this software for your research, please cite the LOESS package of
Cappellari et al. (2013b) <https://ui.adsabs.harvard.edu/abs/2013MNRAS.432.1862C>_,
where the implementation was described. The BibTeX entry for the paper is::
@ARTICLE{Cappellari2013b,
author = {{Cappellari}, M. and {McDermid}, R.~M. and {Alatalo}, K. and
{Blitz}, L. and {Bois}, M. and {Bournaud}, F. and {Bureau}, M. and
{Crocker}, A.~F. and {Davies}, R.~L. and {Davis}, T.~A. and
{de Zeeuw}, P.~T. and {Duc}, P.-A. and {Emsellem}, E. and {Khochfar}, S. and
{Krajnovi{\'c}}, D. and {Kuntschner}, H. and {Morganti}, R. and
{Naab}, T. and {Oosterloo}, T. and {Sarzi}, M. and {Scott}, N. and
{Serra}, P. and {Weijmans}, A.-M. and {Young}, L.~M.},
title = "{The ATLAS$^{3D}$ project - XX. Mass-size and mass-{$\sigma$}
distributions of early-type galaxies: bulge fraction drives kinematics,
mass-to-light ratio, molecular gas fraction and stellar initial mass
function}",
journal = {MNRAS},
eprint = {1208.3523},
year = 2013,
volume = 432,
pages = {1862-1893},
doi = {10.1093/mnras/stt644}
}
install with::
pip install loess
Without writing access to the global site-packages directory, use::
pip install --user loess
To upgrade loess to the latest version use::
pip install --upgrade loess
Full documentation is contained in the individual files docstrings.
Usage examples are contained in the directory loess/examples
which is copied by pip within the global folder
site-packages <https://stackoverflow.com/a/46071447>_.
What follows is the documentation of the two main procedures of the
loess package, extracted from their Python docstrings.
###########################################################################
One-dimensional LOESS smoothing via robust locally-weighted regression.
This function is the implementation by Cappellari et al. (2013) <https://ui.adsabs.harvard.edu/abs/2013MNRAS.432.1862C>_ of the
algorithm by Cleveland (1979) <https://doi.org/10.2307/2286407>_.
.. code-block:: python
xout, yout, wout = loess_1d(x, y, xnew=None, degree=1, frac=0.5,
npoints=None, rotate=False, sigy=None)
x: array_like with shape (n,)
Vector of x coordinate.
y: array_like with shape (n,)
Vector of y coordinate to be LOESS smoothed.
xnew: array_like with shape (m,), optional
Vector of coordinates at which to compute the smoothed y values.
degree: {1, 2}, optional
degree of the local 1-dim polynomial approximation (default degree=1).
frac: float, optional
Fraction of points to consider in the local approximation (default frac=0.5).
Typical values are between frac~0.2-0.8. Note that the values are
weighted by a Gaussian function of their distance from the point under
consideration. This implies that the effective fraction of points
contributing to a given value is much smaller that frac.
npoints: int, optional
Number of points to consider in the local approximation.
This is an alternative to using frac=npoints/x.size.
rotate: bool, optional
Rotate the (x, y) coordinates to have the maximum variance along the
x axis. This is useful to give comparable contribution to the
errors in the x and y variables. It can be used to asses the
sensitivity of the solution to the assumption that errors are only in y.
sigy: array_like with shape (n,)
1-sigma errors for the y values. If this keyword is used
the biweight fit is done assuming those errors. If this keyword
is not used, the biweight fit determines the errors in y
from the scatter of the neighbouring points.
xout: array_like with shape (n,)
Vector of x coordinates for the yout values.
If rotate=False (default) then xout=x.
When passing as input the ``xnew`` coordinates then ``xout=xnew``
and both have shape ``(m,)``.
yout: array_like with shape (n,)
Vector of smoothed y values at the coordinates xout.
When passing as input the ``xnew`` coordinates this contains the
smoothed values at the coordinates ``xnew`` and has shape ``(m,)``.
wout: array_like with shape (n,)
Vector of biweights used in the local regressions. This can be used to
identify outliers: wout=0 for outliers with deviations >4sigma.
When passing as input the ``xnew`` coordinates, this output is
meaningless and is arbitrarily set to unity.
###########################################################################
Two-dimensional LOESS smoothing via robust locally-weighted regression.
This function is the implementation by Cappellari et al. (2013) <https://ui.adsabs.harvard.edu/abs/2013MNRAS.432.1862C>_ of the
algorithm by Cleveland (1979) <https://doi.org/10.2307/2286407>_
for the one-dimensional case and Cleveland & Devlin (1988) <https://doi.org/10.2307/2289282>_ for the two-dimensional case.
.. code-block:: python
zout, wout = loess_2d(x, y, z, xnew=None, ynew=None, degree=1, frac=0.5, npoints=None, rescale=False, sigz=None)
x: array_like with shape (n,)
vector of x coordinates.
y: array_like with shape (n,)
vector of y coordinates.
z: array_like with shape (n,)
vector of z coordinates to be LOESS smoothed.
xnew: array_like with shape (m,), optional
Vector with the x coordinates at which to compute the smoothed
z values.
ynew: array_like with shape (m,), optional
Vector with the y coordinates at which to compute the smoothed
z values.
degree: {1, 2}, optional
degree of the local 2-dim polynomial approximation (default degree=1).
frac: float, optional
Fraction of points to consider in the local approximation (default frac=0.5).
Typical values are between frac~0.2-0.8. Note that the values are
weighted by a Gaussian function of their distance from the point under
consideration. This implies that the effective fraction of points
contributing to a given value is much smaller that frac.
npoints: int, optional
Number of points to consider in the local approximation.
This is an alternative to using frac=npoints/x.size.
rescale: bool, optional
Rotate the (x, y) coordinates to make the x axis the axis of
maximum variance. Subsequently scale the coordinates to have equal
variance along both axes. Then perform the local regressions.
This is recommended when the distribution of points is elongated or
when the units are very different for the two axes.
sigz: array_like with shape (n,)
1-sigma errors for the z values. If this keyword is used
the biweight fit is done assuming these errors. If this keyword
is not used, the biweight fit determines the errors in z
from the scatter of the neighbouring points.
zout: array_like with shape (n,)
Vector of smoothed z values at the coordinates (x, y), or at
(xnew, ynew) if the latter are given as input. In the latter case
zout has shape (m,).
wout: array_like with shape (n,)
Vector of biweights used in the local regressions. This can be used to
identify outliers: wout=0 for outliers with deviations >4sigma.
When passing as input the ``(xnew, ynew)`` coordinates, this output is
meaningless and is arbitrarily set to unity.
###########################################################################
Other/Proprietary License
Copyright (c) 2010-2022 Michele Cappellari
This software is provided as is without any warranty whatsoever. Permission to use, for non-commercial purposes is granted. Permission to modify for personal or internal use is granted, provided this copyright and disclaimer are included in all copies of the software. All other rights are reserved. In particular, redistribution of the code is not allowed.
V2.1.2: MC, Oxford, 31 January 2022
- Fixed incorrect results with integer input coordinates in both
loess_1d and loess_2d. Thanks to Peter Weilbacher (aip.de)
for the report and fix.
V2.1.0: MC, Oxford, 20 July 2021
- Support output coordinates different from the input ones.
- Updated loess_1d_example and loess_2d_example.
V2.0.6: MC, Oxford, 21 May 2018 - Dropped support for Python 2.7.
V2.0.5: MC, Oxford, 18 January 2018 - Fixed FutureWarning in Numpy 1.14.
V2.0.4: MC, Oxford, 18 April 2016 - Fixed deprecation warning in Numpy 1.11.
V2.0.3: MC, Oxford, 8 December 2014 - Updated documentation. Minor polishing.
V2.0.2: MC, Oxford, 3 November 2014 - Returns weights also when frac=0 for consistency.
V2.0.1: MC, Oxford, 10 July 2014 - Removed SciPy dependency.
V2.0.0: MC, Oxford, 26 February 2014 - Translated from IDL into Python.
V1.3.4: MC, Paranal, 7 November 2013 - Include SIGZ and WOUT keywords. Updated documentation.
V1.3.3: MC, Oxford, 31 October 2013 - Use CAP_POLYFIT_2D. - Removed /QUARTIC keyword and replaced by DEGREE keyword like CAP_LOESS_1D.
V1.3.2: MC, Oxford, 12 October 2013 - Test whether input (X,Y,Z) have the same size. - Included NPOINTS keyword.
V1.1.4: MC, Oxford, 16 May 2013 - Updated documentation.
V1.1.3: MC, Oxford, 2 December 2011 - Check when outliers don't change to stop iteration.
V1.1.2: MC, Oxford, 25 July 2011 - Return values unchanged if FRAC=0.
V1.1.1: MC, Oxford, 07 March 2011 - Fix: use ABS() for proper computation of "r".
V1.1.0: MC, Vicenza, 30 December 2010 - Rescale after rotating to axis of maximum variance.
V1.0.0: Michele Cappellari, Oxford, 15 December 2010 - Written and tested.
FAQs
LOESS: smoothing via robust locally-weighted regression in one or two dimensions
We found that loess demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Security News
The Rust Security Response WG is warning of phishing emails from rustfoundation.dev targeting crates.io users.
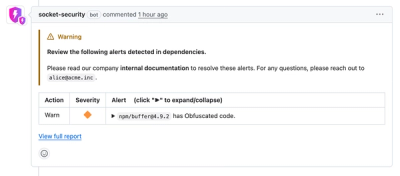
Product
Socket now lets you customize pull request alert headers, helping security teams share clear guidance right in PRs to speed reviews and reduce back-and-forth.

Product
Socket's Rust support is moving to Beta: all users can scan Cargo projects and generate SBOMs, including Cargo.toml-only crates, with Rust-aware supply chain checks.