
Security News
MCP Steering Committee Launches Official MCP Registry in Preview
The MCP Steering Committee has launched the official MCP Registry in preview, a central hub for discovering and publishing MCP servers.
nbmf‑mm implements mean‑parameterized Bernoulli matrix factorization (\Theta = W H \in (0,1)^{M\times N}) with a Majorization–Minimization (MM) solver, following Magron & Févotte (2022). It exposes a scikit‑learn‑style API and two symmetric orientations:
orientation="beta-dir" (default; Original Paper Setting)
W rows sum to 1 (simplex constraint); H is continuous in [0,1] with Beta prior
This matches Magron & Févotte (2022)
orientation="dir-beta" (Symmetric Alternative)
W is continuous in [0,1] with Beta prior; H columns sum to 1 (simplex constraint)
Mathematically equivalent to "beta-dir" on V.T
Projection choices for the simplex‑constrained factor:
projection_method="normalize" (default; theory‑first) – paper‑exact
multiplicative step with the /N (or /M) normalizer that preserves the
simplex in exact arithmetic and enjoys the classical MM monotonicity
guarantee.
projection_method="duchi" (fast) – Euclidean projection to the simplex
(Duchi et al., 2008) performed after the multiplicative step. This is
typically near‑identical to "normalize" numerically, but the formal MM
monotonicity guarantee applies to "normalize".
Masked training (matrix completion) is supported: only observed entries contribute to the likelihood and updates. In the simplex steps the paper‑exact /N (or /M) normalizer is naturally replaced by per‑row (or per‑column) observed counts, preserving the simplex under masking.
pip install nbmf-mm
From source:
pip install "git+https://github.com/siddC/nbmf_mm"
Optional extras:
# scikit-learn integration & NNDSVD-style init (if you enable it later)
pip install "nbmf-mm[sklearn]"
# docs build stack
pip install "nbmf-mm[docs]"
import numpy as np
from nbmf_mm import NBMF
rng = np.random.default_rng(0)
X = (rng.random((100, 500)) < 0.25).astype(float) # binary {0,1} or probabilities in [0,1]
# Theory-first default: monotone MM with paper-exact normalizer
model = NBMF(n_components=6, orientation="beta-dir",
alpha=1.2, beta=1.2, random_state=0).fit(X)
W = model.W_ # shape (n_samples, n_components)
H = model.components_ # shape (n_components, n_features)
Xhat = model.inverse_transform(W) # probabilities in (0,1)
# Transform new data using fixed components H
Y_new = (rng.random((10, 500)) < 0.25).astype(float)
W_new = model.transform(Y_new) # shape (10, n_components)
# Masked training / hold-out validation
mask = (rng.random(X.shape) < 0.9).astype(float) # observe 90% of entries
model = NBMF(n_components=20).fit(X, mask=mask)
print("score (−NLL per observed entry):", model.score(X, mask=mask))
print("perplexity:", model.perplexity(X, mask=mask))
To use the fast projection alternative:
model = NBMF(n_components=6, orientation="beta-dir",
projection_method="duchi", random_state=0).fit(X)
Both orientations solve the Bernoulli likelihood: V ~ Bernoulli(sigmoid(W @ H))
beta-dir (Matches paper's primary formulation)dir-beta (Symmetric formulation)beta-dir on V.TDifferent interpretability needs:
Both solve the same mean-parameterized factorization with symmetric geometric constraints.
NBMF( n_components: int, orientation: {"dir-beta","beta-dir"} = "beta-dir", alpha: float = 1.2, beta: float = 1.2, projection_method: {"normalize","duchi"} = "normalize", max_iter: int = 2000, tol: float = 1e-6, random_state: int | None = None, n_init: int = 1,
use_numexpr: bool = False, use_numba: bool = False, projection_backend: str = "auto", )
random_state (int) for reproducible initialization.n_init > 1 to run several random restarts and keep the best NLL.To reproduce the results from the original paper, use these settings:
from nbmf_mm import NBMF
# Use beta-dir to match paper exactly
model = NBMF(
n_components=10,
orientation="beta-dir",
alpha=1.2,
beta=1.2,
max_iter=500,
tol=1e-5
)
model.fit(X)
# W rows will sum to 1, H will be continuous
Run the reproduction scripts:
python examples/reproduce_magron2022.py
python examples/display_figures.py
J. Duchi, S. Shalev‑Shwartz, Y. Singer, T. Chandra (2008). Efficient Projections onto the ℓ₁‑Ball for Learning in High Dimensions. ICML 2008.
W. Wang, M. Á. Carreira‑Perpiñán (2013). Projection onto the probability simplex: An efficient algorithm with a simple proof, and an application. arXiv:1309.1541.
Bayesian NBMF (related, slower but fully Bayesian):
NBMF project by alumbreras for reference implementations of Bayesian variants.FAQs
Bernoulli (binary) mean-parameterized NMF (NBMF) w/ Majorization–Minimization (MM)
We found that nbmf-mm demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Security News
The MCP Steering Committee has launched the official MCP Registry in preview, a central hub for discovering and publishing MCP servers.
Product
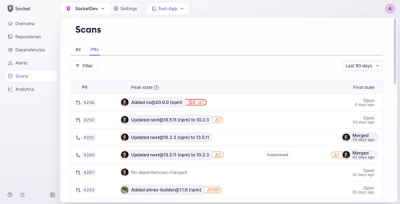
Socket’s new Pull Request Stories give security teams clear visibility into dependency risks and outcomes across scanned pull requests.
Research
/Security News
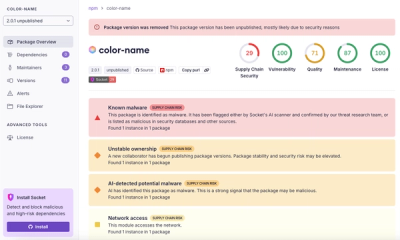
npm author Qix’s account was compromised, with malicious versions of popular packages like chalk-template, color-convert, and strip-ansi published.