Research
/Security News
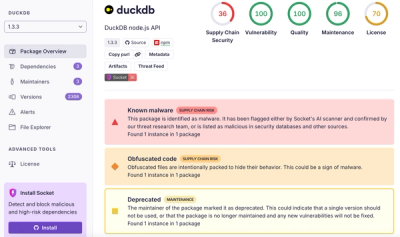
DuckDB npm Account Compromised in Continuing Supply Chain Attack
Ongoing npm supply chain attack spreads to DuckDB: multiple packages compromised with the same wallet-drainer malware.
passagemath <https://github.com/passagemath/passagemath>__ is open
source mathematical software in Python, released under the GNU General
Public Licence GPLv2+.
It is a fork of SageMath <https://www.sagemath.org/>__, which has been
developed 2005-2025 under the motto “Creating a Viable Open Source
Alternative to Magma, Maple, Mathematica, and MATLAB”.
The passagemath fork uses the motto "Creating a Free Passage Between the Scientific Python Ecosystem and Mathematical Software Communities." It was created in October 2024 with the following goals:
clear attribution of upstream projects <https://groups.google.com/g/sage-devel/c/6HO1HEtL1Fs/m/G002rPGpAAAJ>__,platform portability and integration testing services <https://github.com/passagemath/passagemath/issues/704>__
to upstream projects,building a professional, respectful, inclusive community <https://groups.google.com/g/sage-devel/c/xBzaINHWwUQ>__,empowering Sage users to participate in the scientific Python ecosystem <https://github.com/passagemath/passagemath/issues/248>__ by publishing packages,Pyodide <https://pyodide.org/en/stable/>__ for
serverless deployment with Javascript,Full documentation <https://passagemath.org/docs/latest/html/en/index.html>__ is
available online.
passagemath attempts to support and provides binary wheels suitable for all major Linux distributions and recent versions of macOS.
Binary wheels for native Windows (x86_64) are are available for a subset of the passagemath distributions. Use of the full functionality of passagemath on Windows currently requires the use of Windows Subsystem for Linux (WSL) or virtualization.
The supported Python versions in the passagemath 10.6.x series are 3.10.x-3.13.x.
This pip-installable distribution passagemath-gap is a small
distribution that provides modules that depend on the GAP system <https://www.gap-system.org>_.
Cython interface to libgap <https://passagemath.org/docs/latest/html/en/reference/libs/sage/libs/gap/libgap.html>_
Pexpect interface to GAP <https://passagemath.org/docs/latest/html/en/reference/interfaces/sage/interfaces/gap.html>_
numerous modules with build-time dependencies on GAP, see MANIFEST <https://github.com/passagemath/passagemath/blob/main/pkgs/sagemath-gap/MANIFEST.in>_
the binary wheels on PyPI ship a prebuilt copy of GAP and the following GAP packages <https://www.gap-system.org/packages>__:
aclib <https://gap-packages.github.io/aclib/>__: Almost crystallographic groupsalnuth <https://gap-packages.github.io/alnuth>__: Algebraic number theory, interface to PARI/GPatlasrep <https://www.math.rwth-aachen.de/~Thomas.Breuer/atlasrep>__: Interface to the Atlas of Group Representationsautodoc <https://gap-packages.github.io/AutoDoc>__: Generate documentation from GAP source codeautpgrp <https://gap-packages.github.io/autpgrp/>__: Computing the automorphism group of a p-groupcohomolo <https://gap-packages.github.io/cohomolo>__: Cohomology groups of finite groups on finite modulescorelg <https://gap-packages.github.io/corelg/>__: Computing with real Lie algebrascrime <https://gap-packages.github.io/crime/>__: Group cohomology and Massey productscrisp <http://www.icm.tu-bs.de/~bhoeflin/crisp/index.html>__: Computing with radicals, injectors, Schunck classes and projectorscrypting <https://gap-packages.github.io/crypting/>__: Hashes and cryptocryst <https://www.math.uni-bielefeld.de/~gaehler/gap/packages.php>__: Computing with crystallographic groupscrystcat <https://www.math.uni-bielefeld.de/~gaehler/gap/packages.php>__: Crystallographic groups catalogdatastructures <https://gap-packages.github.io/datastructures>__: Collection of standard data structuresdesign <https://gap-packages.github.io/design>__: Constructing, classifying, partitioning, and studying block designsdigraphs <https://digraphs.github.io/Digraphs>__: Graphs, digraphs, and multidigraphsfactint <https://gap-packages.github.io/FactInt>__: Advanced methods for factoring integersfga <https://gap-packages.github.io/fga/>__: Free group algorithmsgapdoc <https://www.math.rwth-aachen.de/~Frank.Luebeck/GAPDoc>__: Meta package for GAP documentationgbnp <https://gap-packages.github.io/gbnp/>__: Gröbner bases of noncommutative polynomialsgenss <https://gap-packages.github.io/genss>__: Generic Schreier-Simsgrape <https://gap-packages.github.io/grape>__: GRaph Algorithms using PErmutation groupsguava <https://gap-packages.github.io/guava>__: Computing with error-correcting codeshap <https://gap-packages.github.io/hap>__: Homological algebra programminghapcryst <https://gap-packages.github.io/hapcryst/>__: HAP extension for crystallographic groupshecke <https://gap-packages.github.io/hecke/>__: Calculating decomposition matrices of Hecke algebrasimages <https://gap-packages.github.io/images/>__: Minimal and canonical imagesjupyterviz <https://nathancarter.github.io/jupyterviz>__: Visualization Tools for Jupyter and the GAP REPLio <https://gap-packages.github.io/io>__: Bindings for low level C library I/O routinesjson <https://gap-packages.github.io/json/>__: Reading and Writing JSONlaguna <https://gap-packages.github.io/laguna>__: Lie AlGebras and UNits of group Algebrasliealgdb <https://gap-packages.github.io/liealgdb/>__: Database of Lie algebrasliepring <https://gap-packages.github.io/liepring/>__: Database and algorithms for Lie p-ringsliering <https://gap-packages.github.io/liering/>__: Computing with finitely presented Lie ringslins <https://gap-packages.github.io/LINS/>__: Computing the normal subgroups of a finitely presented grouploops <https://gap-packages.github.io/loops/>__: Computing with quasigroups and loopsmapclass <https://gap-packages.github.io/MapClass>__: Mapping class orbit computationnq <https://gap-packages.github.io/nq/>__: Nilpotent quotients of finitely presented groupsorb <https://gap-packages.github.io/orb>__: Methods to enumerate orbitspackagemanager <https://gap-packages.github.io/PackageManager/>__: Easily download and install GAP packagespolenta <https://gap-packages.github.io/polenta/>__: Polycyclic presentations for matrix groupspolycyclic <https://gap-packages.github.io/polycyclic/>__: Computation with polycyclic groupspolymaking <https://gap-packages.github.io/polymaking/>__: Interfacing the geometry software polymakeprimgrp <https://gap-packages.github.io/primgrp/>__: Primitive permutation groups libraryquagroup <https://gap-packages.github.io/quagroup/>__: Computations with quantum groupsqpa <https://folk.ntnu.no/oyvinso/QPA/>__: Quivers and path algebrasradiroot <https://gap-packages.github.io/radiroot/>__: Roots of a polynomial as radicalsrepsn <https://gap-packages.github.io/repsn/>__: Constructing representations of finite groupsresclasses <https://gap-packages.github.io/resclasses/>__: Set-theoretic computations with residue classessingular <https://gap-packages.github.io/singular/>__: Interface to Singularsla <https://gap-packages.github.io/sla/>__: Simple Lie algebrassmallgrp <https://gap-packages.github.io/smallgrp/>__: The GAP Small Groups Librarysonata <https://gap-packages.github.io/sonata/>__: System of nearrings and their applicationssophus <https://gap-packages.github.io/sophus/>__: Computing in nilpotent Lie algebrastoric <https://gap-packages.github.io/toric>__: Toric varieties and some combinatorial geometry computationsutils <https://gap-packages.github.io/utils>__: Utility functionsuuid <https://gap-packages.github.io/uuid/>__: RFC 4122 UUIDsZeroMQInterface <https://gap-packages.github.io/ZeroMQInterface/>__: ZeroMQ bindingsthe binary wheels on PyPI ship a prebuilt copy of the native Jupyter kernel for GAP
Running GAP from the command line::
$ pipx run --pip-args="--prefer-binary" --spec "passagemath-gap" sage -gap
┌───────┐ GAP 4.14.0 of 2024-12-05
│ GAP │ https://www.gap-system.org
└───────┘ Architecture: x86_64-apple-darwin22-default64-kv9
Configuration: gmp 6.3.0, GASMAN, readline
Loading the library and packages ...
Packages: GAPDoc 1.6.7, PrimGrp 3.4.4, SmallGrp 1.5.4, TransGrp 3.6.5
Try '??help' for help. See also '?copyright', '?cite' and '?authors'
gap>
Using the library interface from Python::
$ pipx run --pip-args="--prefer-binary" --spec "passagemath-gap[test]" IPython
In [1]: from sage.all__sagemath_modules import *
In [2]: from sage.all__sagemath_gap import *
In [3]: G = libgap.eval("Group([(1,2,3), (1,2)(3,4), (1,7)])")
In [4]: CG = G.ConjugacyClasses()
In [5]: gamma = CG[2]
In [6]: g = gamma.Representative()
In [7]: CG; gamma; g
[ ()^G, (4,7)^G, (3,4,7)^G, (2,3)(4,7)^G, (2,3,4,7)^G, (1,2)(3,4,7)^G, (1,2,3,4,7)^G ]
(3,4,7)^G
(3,4,7)
Jupyter kernel spec
``pip install "passagemath-gap[jupyterkernel]"``
installs the kernel spec for use in the Jupyter notebook and JupyterLab
``pip install "passagemath-gap[notebook]"``
installs the kernel spec and the Jupyter notebook
``pip install "passagemath-gap[jupyterlab]"``
installs the kernel spec and JupyterLab
GAP packages
~~~~~~~~~~~~
``pip install "passagemath-gap[ctbllib]"``
installs `ctbllib <https://www.math.rwth-aachen.de/~Thomas.Breuer/ctbllib>`__: The GAP Character Table Library
``pip install "passagemath-gap[irredsol]"``
installs `irredsol <http://www.icm.tu-bs.de/~bhoeflin/irredsol/index.html>`__: Library of irreducible soluble linear groups over finite fields and of finite primivite soluble groups
``pip install "passagemath-gap[tomllib]"``
installs `tomlib <https://gap-packages.github.io/tomlib>`__: The GAP Library of Tables of Marks
``pip install "passagemath-gap[transgrp]"``
installs `transgrp <https://www.math.colostate.edu/~hulpke/transgrp>`__: Transitive Groups Library
FAQs
passagemath: Computational Group Theory with GAP
We found that passagemath-gap demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 0 open source maintainers collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Research
/Security News
Ongoing npm supply chain attack spreads to DuckDB: multiple packages compromised with the same wallet-drainer malware.

Security News
The MCP Steering Committee has launched the official MCP Registry in preview, a central hub for discovering and publishing MCP servers.
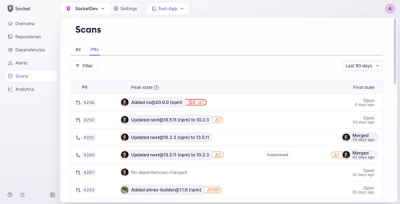
Product
Socket’s new Pull Request Stories give security teams clear visibility into dependency risks and outcomes across scanned pull requests.