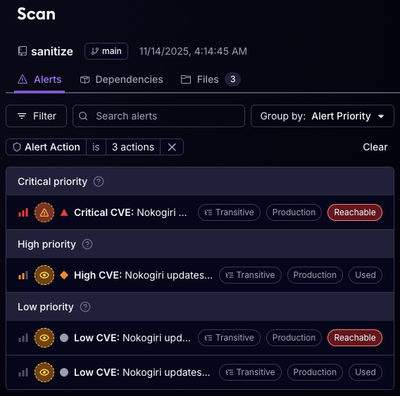
Product
Reachability for Ruby Now in Beta
Reachability analysis for Ruby is now in beta, helping teams identify which vulnerabilities are truly exploitable in their applications.
This is a Python implementation of the NTRUEncrypt algorithm, which is a lattice-based public key encryption scheme that is believed to be resistant to attacks by quantum computers. The implementation is based on the NTRU Prime 4591 parameter set, which provides a security level of approximately 128 bits. The purpose of this implementation is to provide a quantum-proof encryption scheme that can be used to secure sensitive data.
The implementation requires the following Python packages:
To install these packages, you can use the following command:
pip install numpy sympy
You can install it with the reuirements too:
pip install -r requirements.txt
This project can be installed with pip for easy usage.
pip install pq-ntru
import pq_ntru
pq_ntru.generate_keys("key_filename", mode="moderate")
enc = pq_ntru.encrypt("key_filename", "message")
dec = pq_ntru.decrypt("key_filename", enc)
To use the implementation, you can import the ntru module and use the encrypt and decrypt functions to encrypt and decrypt messages, respectively.
git clone https://github.com/protdos/pq-ntru
import NTRU2
NTRU2.generate_keys("test", mode="moderate")
enc = NTRU2.encrypt("test", "hello world")
dec = NTRU2.decrypt("test", enc)
print("Decrypted message:", dec)
The implementation is based on the NTRU Prime 4591 parameter set, which uses a polynomial ring with coefficients in the finite field Z/4591Z. The encryption and decryption algorithms use the NTRU lattice-based encryption scheme, which involves computing a polynomial that is close to a certain lattice point.
The implementation uses the following steps for encryption:
Convert the message to a polynomial with coefficients in the range [-1, 1].
Generate a random polynomial with coefficients in the range [-1, 1] and compute its inverse modulo a certain polynomial.
Compute the product of the message polynomial and the inverse polynomial modulo a certain polynomial, resulting in a new polynomial.
Add noise to the new polynomial to obtain the ciphertext polynomial.
The implementation uses the following steps for decryption:
Compute the product of the ciphertext polynomial and the private key polynomial modulo a certain polynomial, resulting in a new polynomial.
Recover the message polynomial by computing the inverse of the new polynomial modulo a certain polynomial.
NTRUEncrypt is a public key cryptosystem that is based on the mathematical problem of finding a short vector in a lattice. It is believed to be resistant to attacks by quantum computers due to its use of lattice-based cryptography. The security of the system is based on the difficulty of finding short vectors in the lattice, which is a problem that is believed to be hard even for quantum computers.
NTRU was first proposed in 1996 by Hoffstein, Pipher, and Silverman. Since then, several variants of the algorithm have been proposed, including NTRUEncrypt and NTRU Signature. NTRUEncrypt is used for public key encryption, while NTRU Signature is used for digital signatures.
NTRUEncrypt has several benefits over other public key cryptosystems, including:
Resistance to attacks by quantum computers
High performance
Small key sizes
Low bandwidth requirements
Robustness against side-channel attacks
This implementation provides a quantum-proof encryption scheme that can be used to secure sensitive data. The NTRU algorithm is believed to be resistant to attacks by quantum computers and has several benefits over other public key cryptosystems. The implementation is based on the NTRU Prime 4591 parameter set and provides a security level of approximately 128 bits.
FAQs
A quantum proof (post-quantum) implementation of the NTRU algorithm
We found that pq-ntru demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Product
Reachability analysis for Ruby is now in beta, helping teams identify which vulnerabilities are truly exploitable in their applications.
Research
/Security News
Malicious npm packages use Adspect cloaking and fake CAPTCHAs to fingerprint visitors and redirect victims to crypto-themed scam sites.

Security News
Recent coverage mislabels the latest TEA protocol spam as a worm. Here’s what’s actually happening.