pyvpmr

VPMR C++ Implementation

Call For Help

• more performant parallel SVD algorithm: eigen only provides sequential SVD
• alternative integration: currently only Gauss-Legendre quadrature is available

What Is This?

This is a C++ implementation of the VPMR algorithm to compute the approximation of arbitrary smooth kernel. A Python package is also provided.

Check the reference paper 10.1007/s10915-022-01999-1 and the original MATLAB implementation for more details.

In short, the algorithm tries to find a summation of exponentials to approximate a given kernel function. In mathematical terms, it looks for a set of $m_j$ and $s_j$ such that

$$ \max_{t\in{}I}\left|g(t)-\sum_jm_j\exp(-s_jt)\right|<\epsilon. $$

In the above, $g(t)$ is the given kernel function and $\epsilon$ is the prescribed tolerance.

Dependency

The following libraries are required:

• gmp for multiple precision arithmetic
• mpfr for multiple-precision floating-point computations
• tbb for parallel computing

The following libraries are included:

• mpreal mpreal type C++ wrapper, included
• BigInt BigInt arbitrary large integer for combinatorial number, included
• Eigen for matrix decomposition, included
• exprtk for expression parsing, included
• exprtk-custom-types for mpreal support, included

How To

Python Package

[!WARNING] The Python module needs external libraries to be installed.

[!WARNING] Windows users need to have a working MSYS2 environment. See below for more details. For other environments, you need to figure out how to install gmp and mpfr on your own.

On RPM-based Linux distributions (using dnf), if you are:

• compiling the application from source (or wheels are not available), sudo dnf install -y gcc-c++ tbb-devel mpfr-devel gmp-devel
• using the packaged binary (wheels are available), sudo dnf install -y gmp mpfr tbb

On DEB-based Linux distributions (using apt), you need to sudo apt install -y g++ libtbb-dev libmpfr-dev libgmp-dev.

On macOS, you need to brew install tbb mpfr gmp.

Then install the package with pip.

pip install pyvpmr

If the corresponding wheel is not available, the package will be compiled, which takes a few minutes. The execution of the algorithm always requires available gmp, mpfr and tbb libraries.

Jumpstart

import numpy as np

from pyvpmr import vpmr, plot


def kernel(x):
    return np.exp(-x ** 2 / 4)


if __name__ == '__main__':
    m, s = vpmr(n=50, k='exp(-t^2/4)')
    plot(m, s, kernel)

Usage

All available options are:

Usage: vpmr [options]

Options:

    -n, --max-terms             <int>     number of terms (default: 10)
    -c, --max-exponent          <int>     maximum exponent (default: 4)
    -d, --precision-bits        <int>     number of precision bits (default: 512)
    -q, --quadrature-order      <int>     quadrature order (default: 500)
    -m, --precision-multiplier  <float>   precision multiplier (default: 1.5)
    -e, --tolerance             <float>   tolerance (default: 1E-8)
    -k, --kernel                <string>  file name of kernel function (default uses: exp(-t^2/4))
    -s, --singular-values                 print singular values
    -w, --weights                         print weights
    -h, --help                            print this help message

The minimum required precision can be estimated by the parameter $n$. The algorithm involves the computation of $C(4n,k)$ and $2^{4n}$. The number of precision bits shall be at least $4n+\log_2C(4n,2n)$. In the implementation, this number will be further multiplied by the parameter $m$.

Example

The default kernel is exp(-t^2/4). One can run the application with the following command:

./vpmr -n 30

The output is:

Using the following parameters:
       terms = 30.
    exponent = 4.
   precision = 355.
 quad. order = 500.
  multiplier = 1.5000e+00.
   tolerance = 1.0000e-08.
      kernel = exp(-t*t/4).

[1/6] Computing weights... [60/60]
[2/6] Solving Lyapunov equation...
[3/6] Solving SVD...
[4/6] Transforming (P=+9)...
[5/6] Solving eigen decomposition...
[6/6] Done.

M = 
+1.1745193571738943e+01+6.4089561283054790e-107j
-5.5143304351134397e+00+5.7204056791636839e+00j
-5.5143304351134397e+00-5.7204056791636839e+00j
-1.6161617424833762e-02+2.3459542440459513e+00j
-1.6161617424833762e-02-2.3459542440459513e+00j
+1.6338578576177487e-01+1.9308431539218418e-01j
+1.6338578576177487e-01-1.9308431539218418e-01j
-5.4905134221689715e-03+2.2104939243740062e-03j
-5.4905134221689715e-03-2.2104939243740062e-03j
S = 
+1.8757961592204051e+00-0.0000000000000000e+00j
+1.8700580506914817e+00+6.2013413918954552e-01j
+1.8700580506914817e+00-6.2013413918954552e-01j
+1.8521958553280000e+00-1.2601975249082220e+00j
+1.8521958553280000e+00+1.2601975249082220e+00j
+1.8197653300065935e+00+1.9494562062795735e+00j
+1.8197653300065935e+00-1.9494562062795735e+00j
+1.7655956664692953e+00-2.7555720406099038e+00j
+1.7655956664692953e+00+2.7555720406099038e+00j

Running time: 3112 ms.

Arbitrary Kernel

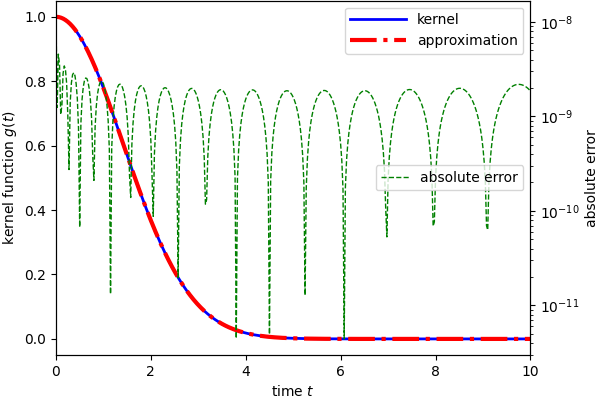
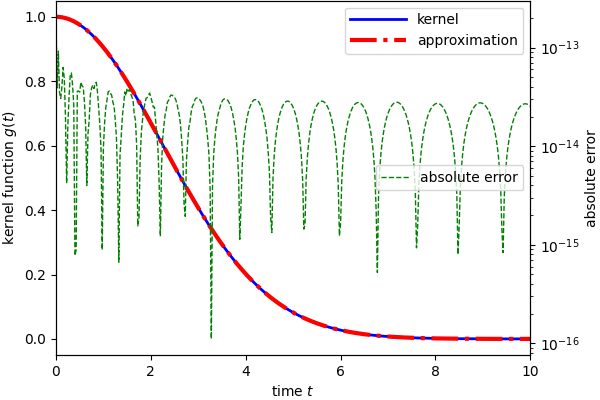
For arbitrary kernel, it is necessary to provide the kernel function in a text file. The file should contain the kernel expressed as a function of variable t.

The exprtk is used to parse the expression and compute the value. The provided kernel function must be valid and supported by exprtk. Check the documentation regarding how to write a valid expression.

For example, to compute the approximation of exp(-t^2/10), one can create a file kernel.txt with the following content:

exp(-t*t/10)

In the following, the kernel function is echoed to a file and then used as an input to the application.

echo "exp(-t*t/10)" > kernel.txt
 ./vpmr -n 60 -k kernel.txt -e 1e-12

Performance

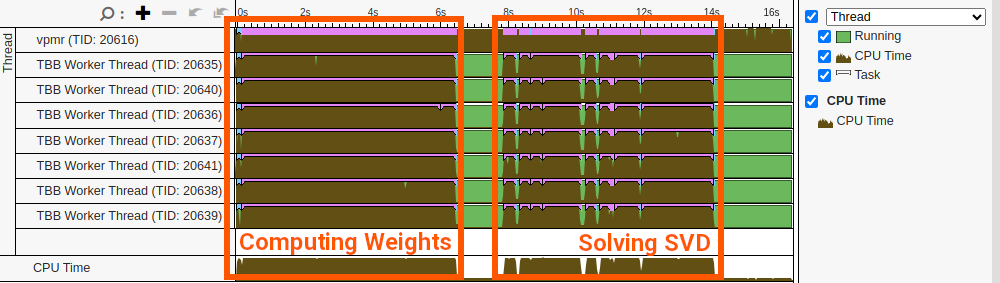
The computation of weights, that involves integrals, and SVD are parallelised. A typical profiling would yield something similar to the following.

Compilation

[!WARNING] The application relies on eigen and exprtk, which depend on very heavy usage of templates. The compilation would take minutes and around 2 GB memory. You need to install libraries gmp, mpfr and tbb before compiling.

Docker

To avoid the hassle of installing dependencies, you can use the provided Dockerfile. For example,

wget -q https://raw.githubusercontent.com/TLCFEM/vpmr/master/Dockerfile
docker build -t vpmr -f Dockerfile .

Or you simply pull using the following command.

docker pull tlcfem/vpmr
# or using GitHub Container Registry
docker pull ghcr.io/tlcfem/vmpr

Windows

Use the following instructions based on MSYS2, or follow the Linux instructions below with WSL.

# install necessary packages
pacman -S git mingw-w64-x86_64-cmake mingw-w64-x86_64-tbb mingw-w64-x86_64-gcc mingw-w64-x86_64-ninja mingw-w64-x86_64-gmp mingw-w64-x86_64-mpfr
# clone the repository
git clone --depth 1 https://github.com/TLCFEM/vpmr.git
# initialise submodules
cd vpmr
git submodule update --init --recursive
# apply patch to enable parallel evaluation of some loops in SVD
cd eigen && git apply --ignore-space-change --ignore-whitespace ../patch_size.patch && cd ..
# configure and compile
cmake -G Ninja -DCMAKE_BUILD_TYPE=Release .
ninja

Linux

The following is based on Fedora.

sudo dnf install gcc g++ gfortran cmake git -y
sudo dnf install tbb-devel mpfr-devel gmp-devel -y
git clone --depth 1 https://github.com/TLCFEM/vpmr.git
cd vpmr
git submodule update --init --recursive
cd eigen && git apply --ignore-space-change --ignore-whitespace ../patch_size.patch && cd ..
cmake -DCMAKE_BUILD_TYPE=Release .
make

Binary

The binary requires available gmp, mpfr and tbb libraries.

❯ ldd vpmr
     linux-vdso.so.1 (0x00007ffcf3121000)
     libgmp.so.10 => /lib64/libgmp.so.10 (0x00007f72087e8000)
     libmpfr.so.6 => /lib64/libmpfr.so.6 (0x00007f7208736000)
     libtbb.so.2 => /lib64/libtbb.so.2 (0x00007f72086f2000)
     libstdc++.so.6 => /lib64/libstdc++.so.6 (0x00007f7208400000)
     libm.so.6 => /lib64/libm.so.6 (0x00007f7208320000)
     libgcc_s.so.1 => /lib64/libgcc_s.so.1 (0x00007f72086d0000)
     libc.so.6 => /lib64/libc.so.6 (0x00007f7208143000)
     /lib64/ld-linux-x86-64.so.2 (0x00007f72088a1000)

The distributed appimage is portable.