treap

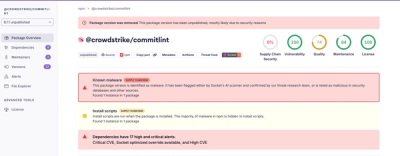
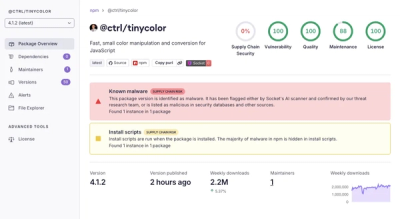
A set of python modules implementing treaps in pure python is provided.

See also my pyx_treap module, which implements treaps in Cython.

Treaps perform most operations in O(log2(n)) time, and are innately sorted. They're very nice for keeping a collection of values that needs to always be sorted, or for optimization problems in which you need to find the p best values out of q, when p is much smaller than q.

A module is provided for treaps that enforce uniqueness.

Example use: .. code-block:: python

>>> import treap
>>> t = treap.treap()
>>> for i in range(6):
...     t[i] = 2**i
...
>>> list(t)
[0, 1, 2, 3, 4, 5]
>>> print(t)
0                                                         5/319487918/32_
1                         2/861020069/4__                                                 _______________
2         1/1135044777/2_                 3/1142319761/8_                 _______________                 _______________
3 0/1473918015/1_ _______________ _______________ 4/2019165697/16 _______________ _______________ _______________ _______________
>>> list(t.items())
[(0, 1), (1, 2), (2, 4), (3, 8), (4, 16), (5, 32)]
>>>

Another example: .. code-block:: python

import treap t = treap.treap() import random for i in range(20): ... t[random.random()] = i ... list(t) [0.011795687154763312, 0.0695864396266509, 0.15741892655439682, 0.18718082546304682, 0.1910965922423038, 0.22849105220538402, 0.276078590851345, 0.3166512089228003, 0.3456516881327997, 0.3543869818366584, 0.4022879538597536, 0.4519316126668157, 0.46329639459896466, 0.4873225275394878, 0.5866856381825849, 0.6403758625610735, 0.6936888466959068, 0.7843975080768091, 0.8888622013819216, 0.9047894146828958] t.find_min() 0.011795687154763312 t.find_max() 0.9047894146828958