
Product
Introducing Rust Support in Socket
Socket now supports Rust and Cargo, offering package search for all users and experimental SBOM generation for enterprise projects.
github.com/alessandro-c/merkle
A merkle tree is a kind of binary tree where each node is labelled with a hash. Starting from the very bottom, leaves will be paired and hashed together to make their parent inner-node, recursively up to the root a.k.a merkle root.
Merkle trees, are commonly used in distributed systems to efficiently compare large data set ensuring validity of such data.
Some examples that leverage merkle trees are the Git version control, AWS's QLDB, Apache's Cassandra and last but not least, blockchains.
There are different flavours of implementations, this package doesn't attempt to build an abstraction for all the possible ones out there, it rather implements a fairly efficient specific one that can be used to experiment with the data structure and concepts.
With that said, if you're looking to use this package to validate merkle proofs for existing blockchains you should look elsewhere as their implementation may be different. For example, Bitcoin's merkle, duplicates eventual odd nodes to re-balance the tree and this implementation doesn't, thus producing a different merkle root and proof.

Generate a new tree, build the proof for a given leaf and verify it.
package main
import (
"crypto/sha256"
"github.com/alessandro-c/merkle"
"hash"
"log"
"math/rand"
"time"
)
func main() {
algo := sha256.New()
leaves := [][]byte{
hashString(algo, "a"), hashString(algo, "b"),
hashString(algo, "c"), hashString(algo, "d"),
hashString(algo, "e"),
}
// you can change the order of leaves without affecting the end result, that is, the same merkle root
rand.Seed(time.Now().UnixNano())
rand.Shuffle(len(leaves), func(i, j int) {
leaves[i], leaves[j] = leaves[j], leaves[i]
})
for i, l := range leaves {
log.Printf("hex leaf #%d - %x\n", i, l)
}
// building up tree up to the merkle root
tree := merkle.NewTree(algo, leaves)
// merkle root
log.Println("hex merkle root: ", tree.Root().Hex())
// building proof for leaf c
hashedLeafToProof := hashString(algo, "c")
proof := tree.Proof(hashedLeafToProof)
for i, h := range proof.ToHexStrings() {
log.Printf("proof for leaf %x at index %d is : %s", hashedLeafToProof, i, h)
}
// verifying proof
ok := merkle.Verify(algo, hashString(algo, "c"), tree.Root().Bytes(), proof.ToByteArrays())
log.Println("proof is valid ?", ok)
}
func hashString(algo hash.Hash, s string) []byte {
algo.Reset()
algo.Write([]byte(s))
return algo.Sum(nil)
}
you can write the whole tree (or sub tree) to a provided io.Writer for example :
// printing whole tree
tree.Root().Graphify(log.Writer())
With output :
3a64c13ffc8d22739538f49d901d909754e4ca185cf128ce7e64c8482f0cd8c6
├── a26df13b366b0fc0e7a96ec9a1658d691d7640668de633333098d7952ce0c50b
│ ├── 28b5a66c8c61ee13ad5f708a561d758b24d10abe5a0e72133c85d59821539e05
│ │ ├── 3e23e8160039594a33894f6564e1b1348bbd7a0088d42c4acb73eeaed59c009d
│ │ └── 3f79bb7b435b05321651daefd374cdc681dc06faa65e374e38337b88ca046dea
│ └── 800e03ddb2432933692401d1631850c0af91953fd9c8f3874488c0541dfcf413
│ ├── 18ac3e7343f016890c510e93f935261169d9e3f565436429830faf0934f4f8e4
│ └── 2e7d2c03a9507ae265ecf5b5356885a53393a2029d241394997265a1a25aefc6
└── ca978112ca1bbdcafac231b39a23dc4da786eff8147c4e72b9807785afee48bb
FAQs
Unknown package
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Product
Socket now supports Rust and Cargo, offering package search for all users and experimental SBOM generation for enterprise projects.
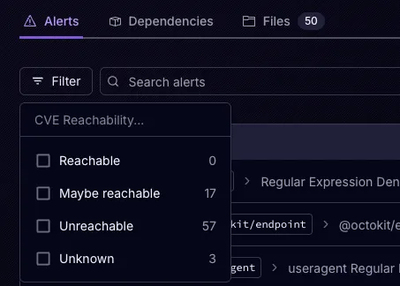
Product
Socket’s precomputed reachability slashes false positives by flagging up to 80% of vulnerabilities as irrelevant, with no setup and instant results.

Product
Socket is launching experimental protection for Chrome extensions, scanning for malware and risky permissions to prevent silent supply chain attacks.