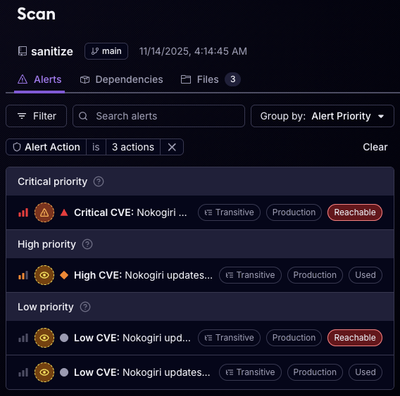
Product
Reachability for Ruby Now in Beta
Reachability analysis for Ruby is now in beta, helping teams identify which vulnerabilities are truly exploitable in their applications.
@m93a/arithmetic-types
Advanced tools
Standardized interfaces for mathematical data types, such as Complex, Fraction and Matrix. This repository is a draft, the standard has not been adopted anywhere yet.
Arithmetics object with static methods such as add(x, y) which accept arguments of a single data type and perform arithmetic operations on it.scalar-arithmetic.ts and tensor-arithmetic.ts.Arithmetics must treat the arguments as immutable and return a new instance where applicable.x.clone() method and a reference to the Arithmetics object using x[Symbol.for('arithmetics')].x.add(y); if they do, these arithmetic methods should be mutating.
this, ie. x.add(y) returns the mutated x.(The words must, should and may follow RFC2119)
This is how one can implement an arithmetic and geometric mean for fractions, decimals, complex numbers and quaternions etc., regardless of their implementation.
import { NormedDivisionRing, InstanceOf, symbols } from 'arithmetic-types'
const { Arithmetics } = symbols
type Numeric<T, F> = InstanceOf< NormedDivisionRing<T, F> >
function arithmeticMean<T, F>(first: Numeric<T, F>, ...args: Numeric<T, F>[])
{
const arithmetics = first[Arithmetics]
const sum = args.reduce( (a, b) => arithmetics.add(a, b), first )
const count = args.length + 1
return arithmetics.scale(sum, 1/count)
}
function geometricMean<T, F>(first: Numeric<T, F>, ...args: Numeric<T, F>[])
{
const arithmetics = first[Arithmetics]
if (!arithmetics.isCommutative) throw new TypeError('Geometric mean of non-commutative numbers is not supported.')
const product = args.reduce( (a, b) => arithmetics.mul(a, b), first )
const count = args.length + 1
return arithmetics.pow(product, 1/count)
}
This is also an implementation of arithmetic and geometric mean, this time for the data types which support instance methods. This code is potentially faster than the previous one, because it doesn't have to create a new instance for every arithmetic operartion.
import { NormedDivisionRing, InstanceWithMethods } from 'arithmetic-types'
type Numeric<T, F> = InstanceWithMethods< T, NormedDivisionRing<T, F> >
function arithmeticMean<T, F>(first: Numeric<T, F>, ...args: Numeric<T, F>[])
{
const sum = first.clone()
args.forEach( a => sum = sum.add(a) )
sum = sum.scale( 1/(args.length + 1) )
return sum
}
function geometricMean<T, F>(first: Numeric<T, F>, ...args: Numeric<T, F>[])
{
if (!first[Arithmetics].isCommutative) throw new TypeError('Geometric mean of non-commutative numbers is not supported.')
const product = first.clone()
args.forEach( a => product = product.mul(a) )
product = product.pow( 1/(args.length + 1) )
return product
}
FAQs
Interfaces for mathematical data-types to implement
The npm package @m93a/arithmetic-types receives a total of 2 weekly downloads. As such, @m93a/arithmetic-types popularity was classified as not popular.
We found that @m93a/arithmetic-types demonstrated a not healthy version release cadence and project activity because the last version was released a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Product
Reachability analysis for Ruby is now in beta, helping teams identify which vulnerabilities are truly exploitable in their applications.
Research
/Security News
Malicious npm packages use Adspect cloaking and fake CAPTCHAs to fingerprint visitors and redirect victims to crypto-themed scam sites.

Security News
Recent coverage mislabels the latest TEA protocol spam as a worm. Here’s what’s actually happening.