Research
/Security News
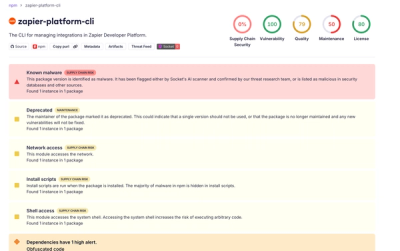
Shai Hulud Strikes Again (v2)
Another wave of Shai-Hulud campaign hits npm.
A TypeScript implementation of Dijkstra's algorithm for finding shortest paths in graphs
A TypeScript implementation of Dijkstra's algorithm for finding shortest paths in graphs.

npm install djikstra
import Djikstra from 'djikstra';
// Create a graph as an adjacency list
const graph = {
A: { B: 5, C: 2 },
B: { A: 5, D: 1 },
C: { A: 2, D: 6 },
D: { B: 1, C: 6, E: 2 },
E: { D: 2 },
};
const pathfinder = new Djikstra();
// Find shortest path between two nodes
const result = pathfinder.findShortestPath(graph, 'A', 'E');
if (result.status === 'reachable') {
console.log(`Path found: ${result.path.join(' → ')}`);
console.log(`Total distance: ${result.distance}`);
} else {
console.log('No path exists to the destination');
}
// Compute distances to all nodes
const allDistances = pathfinder.computeAllPaths(graph, 'A');
console.log(allDistances);
// Output: { A: 0, B: 5, C: 2, D: 6, E: 8 }
// Compute both distances and paths
const fullResult = pathfinder.computeDistancesAndPaths(graph, 'A');
console.log(fullResult);
// Output: {
// distances: { A: 0, B: 5, C: 2, D: 6, E: 8 },
// predecessors: { B: 'A', C: 'A', D: 'B', E: 'D' }
// }
This library implements Dijkstra's algorithm using a binary min-heap priority queue for performance optimization. Here's what you should know about our implementation:
Graphs are represented as adjacency lists using plain JavaScript objects:
// Graph structure
interface Graph {
[node: string]: {
[neighbor: string]: number
}
}
Each key in the outer object represents a node in the graph. The value is another object where:
Example for a road network:
const roadNetwork = {
// Each city with its connections
"NewYork": {
"Boston": 215, // Distance in miles
"Philadelphia": 95
},
"Boston": {
"NewYork": 215,
"Portland": 112
},
"Philadelphia": {
"NewYork": 95,
"Washington": 140
},
"Portland": {
"Boston": 112
},
"Washington": {
"Philadelphia": 140
}
};
For a weighted graph:
The Dijkstra class provides three main methods for pathfinding:
findShortestPath(graph: Graph, source: string, destination: string): PathResult
Calculates the shortest path between two nodes in a graph.
| Parameter | Type | Description |
|---|---|---|
| graph | Graph | The graph represented as an adjacency list |
| source | string | The starting node ID |
| destination | string | The target node ID |
Returns: A discriminated union with either reachable or unreachable status
type PathResult =
| { status: 'reachable'; path: string[]; distance: number }
| { status: 'unreachable' }
Throws: Error only if the source node doesn't exist in the graph
computeAllPaths(graph: Graph, source: string): Record<string, number>
Computes the shortest distance from a source to all reachable nodes.
| Parameter | Type | Description |
|---|---|---|
| graph | Graph | The graph represented as an adjacency list |
| source | string | The starting node ID |
Returns: An object mapping each node ID to its distance from the source
computeDistancesAndPaths(
graph: Graph,
source: string
): {
distances: Record<string, number>;
predecessors: Record<string, string>
}
Provides complete pathfinding information from a source to all nodes.
| Parameter | Type | Description |
|---|---|---|
| graph | Graph | The graph represented as an adjacency list |
| source | string | The starting node ID |
Returns:
distances: Maps each node ID to its shortest distance from sourcepredecessors: Maps each node ID to its predecessor in the shortest pathNote: Use the predecessors map to reconstruct the full path to any node
ISC
FAQs
A TypeScript implementation of Dijkstra's algorithm for finding shortest paths in graphs
We found that djikstra demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Research
/Security News
Another wave of Shai-Hulud campaign hits npm.

Product
Add real-time Socket webhook events to your workflows to automatically receive software supply chain alert changes in real time.
Security News
ENISA has become a CVE Program Root, giving the EU a central authority for coordinating vulnerability reporting, disclosure, and cross-border response.