Research
/Security News
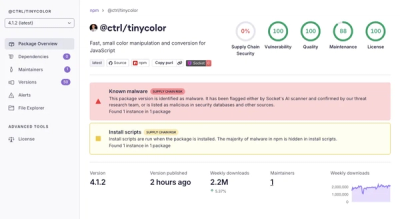
Popular Tinycolor npm Package Compromised in Supply Chain Attack Affecting 40+ Packages
Malicious update to @ctrl/tinycolor on npm is part of a supply-chain attack hitting 40+ packages across maintainers
average-minimum-distance
Advanced tools
This package implements pointwise distance distributions (PDD), geometry-based crystal descriptors designed to have desirable properties such as independence from choice of a unit cell and continuity under perturbations of points. The average of PDD, the average minimum distance (AMD), shares these properties while being significantly faster to compare.
The typical representation of a crystal as a motif and unit cell is ambiguous, because many choices of cell and motif can define the same crystal. This package implements descriptors which are isometry invariants, meaning they are always the same for any two crystals which are geometrically equivalent, independent of a choice of unit cell and motif. These invariants can be compared to give a distance between crystals, which is 0 for identical crystals and close to 0 for similar crystals (a continuous metric).
The pointwise distance distribution records the environment of each atom in a unit cell by listing distances to neighbouring atoms in order. Two PDDs are compared using an optimal matching algorithm (earth mover's distance). Taking the average of a PDD gives a vector called the average minimum distance (AMD), which are simpler and faster to compare but still identify crystals with similar geometry. Both have one parameter k, equal to the number of neighbouring atoms considered for each atom in the unit cell.
Use pip to install average-minimum-distance:
pip install average-minimum-distance
Then import average-minimum-distance with import amd.
The following code extracts a crystal from two CIF files and compares them by their pointwise distance distributions (PDD, neighbouring atoms k=100):
import amd
# read
crystal1 = amd.CifReader('crystal1.cif').read()
crystal2 = amd.CifReader('crystal2.cif').read()
# calculate PDDs
k = 100
pdd1 = amd.PDD(crystal1, k)
pdd2 = amd.PDD(crystal2, k)
distance = amd.EMD(pdd1, pdd2)
Earth mover's distance (EMD) is the comparison metric used between PDDs. The .read() function of the :class:amd.CifReader <amd.io.CifReader> returns
one crystal (a :class:amd.PeriodicSet <amd.periodicset.PeriodicSet> object) if
only one is present in the CIF, otherwise it returns a list.
CSD Python API only: CSD entries can be accessed via the CSD Python API if it's installed with amd.CSDReader, see the documentation for details. :class:amd.CifReader <amd.io.CifReader> can accept file formats other than CIF by passing reader='ccdc'.
The following extracts collections of crystals from two CIF files and makes PDD and AMD distance matrices:
import amd
import numpy as np
# read
crystals1 = list(amd.CifReader('crystals1.cif'))
crystals2 = list(amd.CifReader('crystals2.cif'))
# calculate PDD
k = 100
pdds1 = [amd.PDD(crystal, k) for crystal in crystals1]
pdds2 = [amd.PDD(crystal, k) for crystal in crystals2]
# distance matrix of EMDs between PDDs in each set
pdd_dm = amd.PDD_cdist(pdds1, pdds2)
# the above line is equivalent to:
pdd_dm = np.empty((len(pdds1), len(pdds2)), dtype=np.float64)
for i, pdd1 in enumerate(pdds1):
for j, pdd2 in enumerate(pdds2):
pdd_dm[i, j] = amd.EMD(pdd1, pdd2)
# calculates AMD from PDD, can be calculated from scratch with amd.AMD()
amds1 = [amd.PDD_to_AMD(pdd) for pdd in pdds1]
amds2 = [amd.PDD_to_AMD(pdd) for pdd in pdds2]
# distance matrix between AMDs, default metric is "chebyshev" (L-infinity)
amd_dm = amd.AMD_cdist(amds1, amds2)
The average minimum distance (AMD) is given by amd.AMD(), which returns a vector instead of a matrix. These vectors can be compared by any metric on vectors, but the function amd.AMD_cdist() is a convenient function to batch compare AMDs in the same way as amd.PDD_cdist() above (essentially a wrapper of SciPy's cdist).
The functions amd.PDD_pdist() and amd.AMD_pdist() also exist
to compare one collection of crystals pairwise and return a condensed distance matrix like
SciPy's pdist.
The parameter k is the number of neighbouring atoms considered for each atom in a unit cell. Two crystals with the same unit molecule will have a small PDD/AMD distance for small enough k (e.g. k = 3), and a larger k means the geometry must be similar up to a larger radius for the distance to be small. The default we generally use is k = 100, but if this is significantly less than the number of atoms in the unit molecule, consider using a larger value. It is usually not useful to choose k too large (many times larger than the number of atoms in a unit cell).
The following plots a single linkage dendrogram of crystals in a CIF using AMD:
import amd
import matplotlib.pyplot as plt
from scipy.cluster import hierarchy
crystals = list(amd.CifReader('crystals.cif'))
names = [crystal.name for crystal in crystals]
amds = [amd.AMD(crystal, 100) for crystal in crystals]
cdm = amd.AMD_pdist(amds)
Z = hierarchy.linkage(cdm, 'single')
dn = hierarchy.dendrogram(Z, labels=names)
plt.show()
For more examples, see the Jupyter notebook in the examples folder.
Use the following bib references to cite our work.
Average minimum distances of periodic point sets - foundational invariants for mapping periodic crystals. MATCH Communications in Mathematical and in Computer Chemistry, 87(3), 529-559 (2022). https://doi.org/10.46793/match.87-3.529W.
@article{widdowson2022average,
title = {Average Minimum Distances of periodic point sets - foundational invariants for mapping periodic crystals},
author = {Widdowson, Daniel and Mosca, Marco M and Pulido, Angeles and Kurlin, Vitaliy and Cooper, Andrew I},
journal = {MATCH Communications in Mathematical and in Computer Chemistry},
doi = {10.46793/match.87-3.529W},
volume = {87},
number = {3},
pages = {529-559},
year = {2022}
}
Resolving the data ambiguity for periodic crystals. Advances in Neural Information Processing Systems (NeurIPS 2022), v.35. https://openreview.net/forum?id=4wrB7Mo9_OQ.
@inproceedings{widdowson2022resolving,
title = {Resolving the data ambiguity for periodic crystals},
author = {Widdowson, Daniel and Kurlin, Vitaliy},
booktitle = {Advances in Neural Information Processing Systems},
year = {2022},
url = {https://openreview.net/forum?id=4wrB7Mo9_OQ}
}
FAQs
Descriptors of crystals based on geometry (isometry invariants).
We found that average-minimum-distance demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Research
/Security News
Malicious update to @ctrl/tinycolor on npm is part of a supply-chain attack hitting 40+ packages across maintainers

Security News
pnpm's new minimumReleaseAge setting delays package updates to prevent supply chain attacks, with other tools like Taze and NCU following suit.

Security News
The Rust Security Response WG is warning of phishing emails from rustfoundation.dev targeting crates.io users.