Dual quaternions are a way of representing rigid body transformations, just like homogeneous transformations do. Instead of using a 4x4 matrix, the transformation is represented as two quaternions. This has several advantages, which are listed under Why use dual quaternions?. The term 'dual' refers to dual number theory, which allows representing numbers (or in this case quaternions) very similar to complex numbers, with the difference being that i or j becomes e (epsilon), and instead of i^2 = -1, we have e^2 = 0. This allows, for example, the multiplication of two dual quaternions to work in the same way as homogeneous matrix multiplication.
For more information on dual quaternions, take a look at the References. For conversion from and to common ROS messages, see dual_quaternions_ros.
pip install dual_quaternions
from dual_quaternions import DualQuaternion
Many libraries focus on efficiency and are written in C++, sometimes with Python bindings. They typically do not include tests and so it's hard to know whether they're accurate. Along with a test suite, this library aims to explain the various functions and why they're implemented that way. As a result it serves as a starting point for those trying to get started with dual quaternions.
The exponential map is a map from the tangent space at some point x on the manifold onto its Lie group. It maps a vector $s$ such that the geodesic through $x$ is followed. At the identity, $exp_1(s) =: exp(s)$ where $s$ is a pure dual quaternion (real part of $q_r$ and $q_d$ are zero) At some point $x$, using parallel transport the map becomes $\exp_x(s) = x \cdot \exp_1(x^{-1} \cdot s)$ Intuitively, because $\exp$ is only defined at the identity but we're trying to find the map at some other point $x$, we first move it to the origin by premultiplying with $x^{-1}$. Then we map it to the manifold/Lie group using the exponential map, and finally move it back to $x$ by premultiplying by $x$.
In some sources log and exp are derived using the Taylor method first order approximation $f(a+\epsilon b) ~= f(a)+\epsilon b f'(a)$ Applying this to the log and exp functions, you would get:
exp(r+\epsilon d) = exp(r)+\epsilon \cdot exp(r) \cdot d \\
log(r+\epsilon d) = log(r)+\epsilon \cdot r^{-1}\cdot d
where $r^{-1}=r^$ since $r$ is unit. This only gives the same answer as the Lie algebra formulation when the dual part is symmetric with respect to the real part, i.e. $d \cdot r^ = r^* \cdot d$ For nontrivial rotation and translation not aligned with the rotation axis, this is not the case. This is because the Taylor approximation assumes commutativity, which dual quaternion multiplication is not. As a result, the Taylor method can produce non-symmetric, non-pure dual quaternions which is not 'correct'.
FAQs
Dual quaternion implementation
We found that dual-quaternions demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?
Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.
Security News
/Research
Malicious npm package impersonates Nodemailer and drains wallets by hijacking crypto transactions across multiple blockchains.
Security News
This episode explores the hard problem of reachability analysis, from static analysis limits to handling dynamic languages and massive dependency trees.
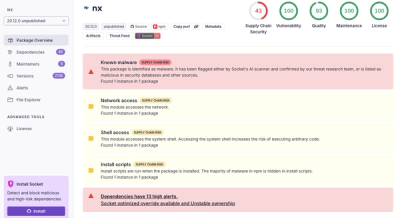
Security News
/Research
Malicious Nx npm versions stole secrets and wallet info using AI CLI tools; Socket’s AI scanner detected the supply chain attack and flagged the malware.