Product
Announcing Precomputed Reachability Analysis in Socket
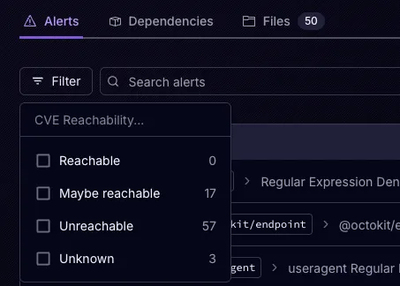
Socket’s precomputed reachability slashes false positives by flagging up to 80% of vulnerabilities as irrelevant, with no setup and instant results.
A Python Flexible Modeler for Optimization Problems.
flopt is a modeling tool for optimization problems such as LP, QP, Ising, QUBO, etc. flopt provides various functions for flexible and easy modeling. Users can also solve modeled problems with several solvers to obtain optimal or good solutions.
documentation | tutorial | case studies
PyPI
pip install flopt
GitHub
git clone https://github.com/flab-coder/flopt.git
cd flopt && python -m pip install .
minimize 2*(3*a+b)*c**2 + 3
s.t a + b * c <= 3
0 <= a <= 1
1 <= b <= 2
c <= 3
minimize simulator(a, b, c)
s.t 0 <= a <= 1
1 <= b <= 2
1 <= c <= 3
You can write codes like PuLP application.
from flopt import Variable, Problem
# Variables
a = Variable('a', lowBound=0, upBound=1, cat='Continuous')
b = Variable('b', lowBound=1, upBound=2, cat='Continuous')
c = Variable('c', upBound=3, cat='Continuous')
# Problem
prob = Problem()
prob += 2 * (3*a+b) * c**2 + 3 # set the objective function
prob += a + b * c <= 3 # set the constraint
# Solve
prob.solve(timelimit=0.5, msg=True) # run solver to solve the problem
# display the result, incumbent solution
print('obj value', prob.getObjectiveValue())
print('a', a.value())
print('b', b.value())
print('c', c.value())
In addition, you can represent any objective function by CustomExpression
from flopt import Variable, Problem, CustomExpression
# Variables
a = Variable('a', lowBound=0, upBound=1, cat='Integer')
b = Variable('b', lowBound=1, upBound=2, cat='Continuous')
def user_func(a, b):
from math import sin, cos
return (0.7*a + 0.3*cos(b)**2 + 0.1*sin(b))*abs(a)
custom_obj = CustomExpression(func=user_func, args=[a, b])
prob = Problem(name='CustomExpression')
prob += custom_obj
# Solve
prob.solve(timelimit=1, msg=True) # run solver to solve the problem
# display the result, incumbent solution
print('obj value', prob.getObjectiveValue())
In the case you solve TSP, Permutation Variable is useful.
from flopt import Variable, Problem, CustomExpression
N = 4 # Number of city
D = [[0,1,2,3], # Distance matrix
[3,0,2,1],
[1,2,0,3],
[2,3,1,0]]
# Variables
x = Variable('x', lowBound=0, upBound=N-1, cat='Permutation')
# Object
def tsp_dist(x):
distance = 0
for head, tail in zip(x, x[1:]+[x[0]]):
distance += D[head][tail] # D is the distance matrix
return distance
tsp_obj = CustomExpression(func=tsp_dist, args=[x])
# Problem
prob = Problem(name='TSP')
prob += tsp_obj
# Solve
prob.solve(timelimit=10, msg=True) # run solver to solve the problem
# display the result, incumbent solution
print('obj value', prob.getObjectiveValue())
print('x', x.value())
FAQs
A python Non-Linear Programming API with Heuristic approach
We found that flopt demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Product
Socket’s precomputed reachability slashes false positives by flagging up to 80% of vulnerabilities as irrelevant, with no setup and instant results.

Product
Socket is launching experimental protection for Chrome extensions, scanning for malware and risky permissions to prevent silent supply chain attacks.

Product
Add secure dependency scanning to Claude Desktop with Socket MCP, a one-click extension that keeps your coding conversations safe from malicious packages.