gnssmultipath

GNSS Multipath Analysis

Table of Contents

• Introduction

• Features

• Installation

  • Prerequisites
  • Installing LaTeX (optional)

• How to run it

• Compatibility

• License

• User arguments

• Examples

  • Run a multipath analysis using a SP3 file and only mandatory arguments
  • Run a multipath analysis using a RINEX navigation file with SNR, a defined datarate for ephemerides and with an elevation angle cut off at 10°
  • Run analysis with several navigation files
  • Run analysis without making plots
  • Run analysis and use the Zstandard compression algorithm (ZSTD) to compress the pickle file storing the results
  • Read a RINEX observation file
  • Read a RINEX navigation file (v.3)
  • Read in the results from an uncompressed Pickle file
  • Read in the results from a compressed Pickle file
  • Estimate the receiver position based on pseudoranges using SP3 file and print the standard deviation of the estimated position
  • Estimate the receiver position based on pseudoranges using RINEX navigation file and print the DOP values

• Background information about implementation

  • Converting Keplerian Elements to ECEF Coordinates
  • Interpolating a GLONASS State Vector to ECEF Coordinates
  • Interpolating Precise Satellite Coordinates from SP3 file Using Neville's Algorithm
  • Estimating the Receiver Position Using Least Squares
  • Statistical Parameters of the estimated position

Introduction

GNSS Multipath Analysis is a software tool for analyzing the multipath effect on Global Navigation Satellite Systems (GNSS). The core functionality is based on the MATLAB software GNSS_Receiver_QC_2020, but has been adapted to Python and includes additional features. A considerable part of the results has been validated by comparing the results with estimates from RTKLIB. This software will be further developed, and feedback and suggestions are therefore gratefully received. Don't hesitate to report if you find bugs or missing functionality. Either by e-mail or by raising an issue here in GitHub.

Features

• Estimates the code multipath for all GNSS systems (GPS, GLONASS, Galileo, and BeiDou).
• Estimates the code multipath for all available signals/codes in the RINEX file.
• Provides statistics on the total number of cycle slips detected (using both ionospheric residuals and code-phase differences).
• Supports both RINEX navigation files (broadcast ephemerides) and SP3 files (precise ephemerides).
• Supports both RINEX v2.xx and v3.xx observation files.
• Generates various plots, including:
  • Ionospheric delay over time and zenith-mapped ionospheric delay (combined).
  • The multipath effect plotted against time and elevation angle (combined).
  • Bar plot showing multipath RMSE for each signal and system.
  • Polar plot of the multipath effect and Signal-to-Noise Ratio (SNR).
  • Polar plots of SNR and multipath.
  • Polar plot of each observed satellite in the system.
  • SNR versus time/elevation.
• Extracts GLONASS FCN from RINEX navigation files.
• Detects cycle slips and estimates the multipath effect.
• Exports results to CSV and a Python dictionary as a Pickle (both compressed and uncompressed formats are supported).
• Allows selection of specific navigation systems and signal bands for analysis.
• Estimate the approximate position of the receiver using pseudoranges from the RINEX observation file.
  • Supports both SP3 and RINEX navigation files.
  • The software will estimate the receiver's position if it is not provided in the header of the RINEX observation file.
  • Supports user-defined Coordinate Reference System (CRS). The estimated coordinates can be delivered in the desired CRS.
  • Calculates statistical measures for the estimated position, including:
    • Residuals
    • Sum of Squared Errors (SSE)
    • Cofactor matrix
    • Covariance matrix
    • Dilution of Precision (PDOP, GDOP, and TDOP)
    • Standard deviation of the estimated position

Installation

To install the software to your Python environment using pip:

pip install gnssmultipath

Prerequisites

• Python >=3.8: Ensure you have Python 3.8 or newer installed.
• LaTeX (optional): Required for generating plots with LaTeX formatting.

Note: In the example plots, TEX is used to get prettier text formatting. However, this requires TEX/LaTex to be installed on your computer. The program will first try to use TEX, and if it's not possible, standard text formatting will be used. So TEX/LaTex is not required to run the program and make plots.

Installing LaTeX (optional)

• On Ubuntu: sudo apt-get install texlive-full
• On Windows: Download and install from MiKTeX
• On MacOS: brew install --cask mactex

How to Run It

To run the GNSS Multipath Analysis, import the main function and specify the RINEX observation and navigation/SP3 files you want to use. To perform the analysis with default settings and by using a navigation file:

from gnssmultipath import GNSS_MultipathAnalysis

outputdir = 'path_to_your_output_dir'
rinObs_file = 'your_observation_file.XXO'
rinNav_file = 'your_navigation_file.XXN'
analysisResults = GNSS_MultipathAnalysis(rinObs_file,
                                         broadcastNav1=rinNav_file,
                                         outputDir=outputdir)

If you have a SP3 file, and not a RINEX navigation file, you just replace the keyword argument broadcastNav1 with sp3NavFilename_1.

The steps are:

• Reads in the RINEX observation file
• Reads the RINEX navigation file or the precise satellite coordinates in SP3-format (depends on what’s provided)
• If a navigation file is provided, the satellite coordinates will be transformed from Kepler-elements to ECEF for GPS, Galileo and BeiDou. For GLONASS the navigation file is containing a state vector. The coordinates then get interpolated to the current epoch by solving the differential equation using a 4th order Runge-Kutta. If a SP3 file is provided, the interpolation is done using Neville's algorithm.
• Compute the satellites' elevation and azimuth angles. If the receiver's approximate position is not provided in the header of the RINEX observation file, the software automatically estimates it based on pseudoranges using the GNSSPositionEstimator class.
• Cycle slip detection by using both ionospheric residuals and a code-phase combination. These linear combinations are given as

$$ \dot{I} = \frac{1}{\alpha-1}\left(\Phi_1 - \Phi_2\right)/\Delta t $$

$$ d\Phi_1R_1 = \Phi_1 - R_1 $$

The threshold values can be set by the user, and the default values are set to $0.0667 [\frac{m}{s}]$ and $6.67[\frac{m}{s}]$ for the ionospheric residuals and code-phase combination respectively.

• Multipath estimates get computed by making a linear combination of the code and phase observation. PS: A dual frequency receiver is necessary because observations from two different bands/frequency are needed.

$$MP_1 = R_1 - \left(1+\frac{2}{\alpha - 1}\right)\Phi_1 + \left(\frac{2}{\alpha - 1}\right)\Phi_2$$

where $R_1$ is the code observation on band 1, $\Phi_1$ and $\Phi_2$ is phase observation on band 1 and band 2 respectively. Furthermore $\alpha$ is the ratio between the two frequency squared

$$\alpha=\frac{{f}^2_1}{{f}^2_2}$$

• Based on the multipath estimates computed in step 6, both weighted and unweighted RMS-values get computed. The RMS value has unit meter, and is given by

$$RMS=\sqrt{\frac{\sum\limits_{i=1}^{N_{sat}}\sum\limits_{j=1}^{N_{epohcs}} MP_{ij}}{N_{est}}}$$

For the weighted RMS value, the satellite elevation angle is used in a weighting function defined as

$$w =\frac{1}{4sin^2\beta}$$

for every estimates with elevation angle $\beta$ is below $30^{\circ}$ and $w =1$ for $\beta > 30^{\circ}$.

• Several plot will be generated (if not set to FALSE):

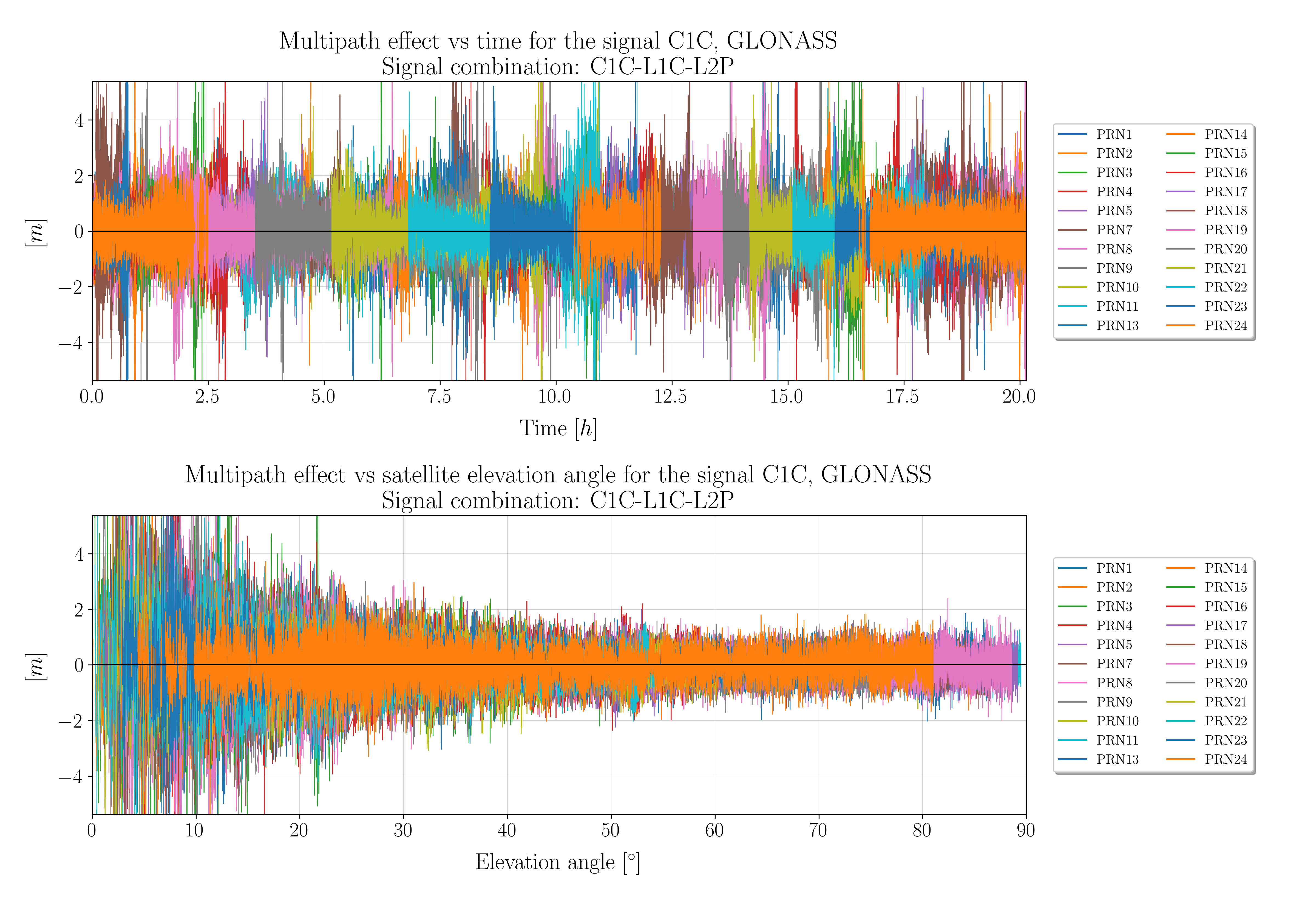
  • Ionospheric delay wrt time and zenith mapped ionospheric delay (combined)

    

  • The Multipath effect plotted wrt time and elevation angle (combined)

    

  • Barplot showing RMS values for each signal and system

    

  • Polar plot of the multipath effect as function of elevation angle and azimuth

    

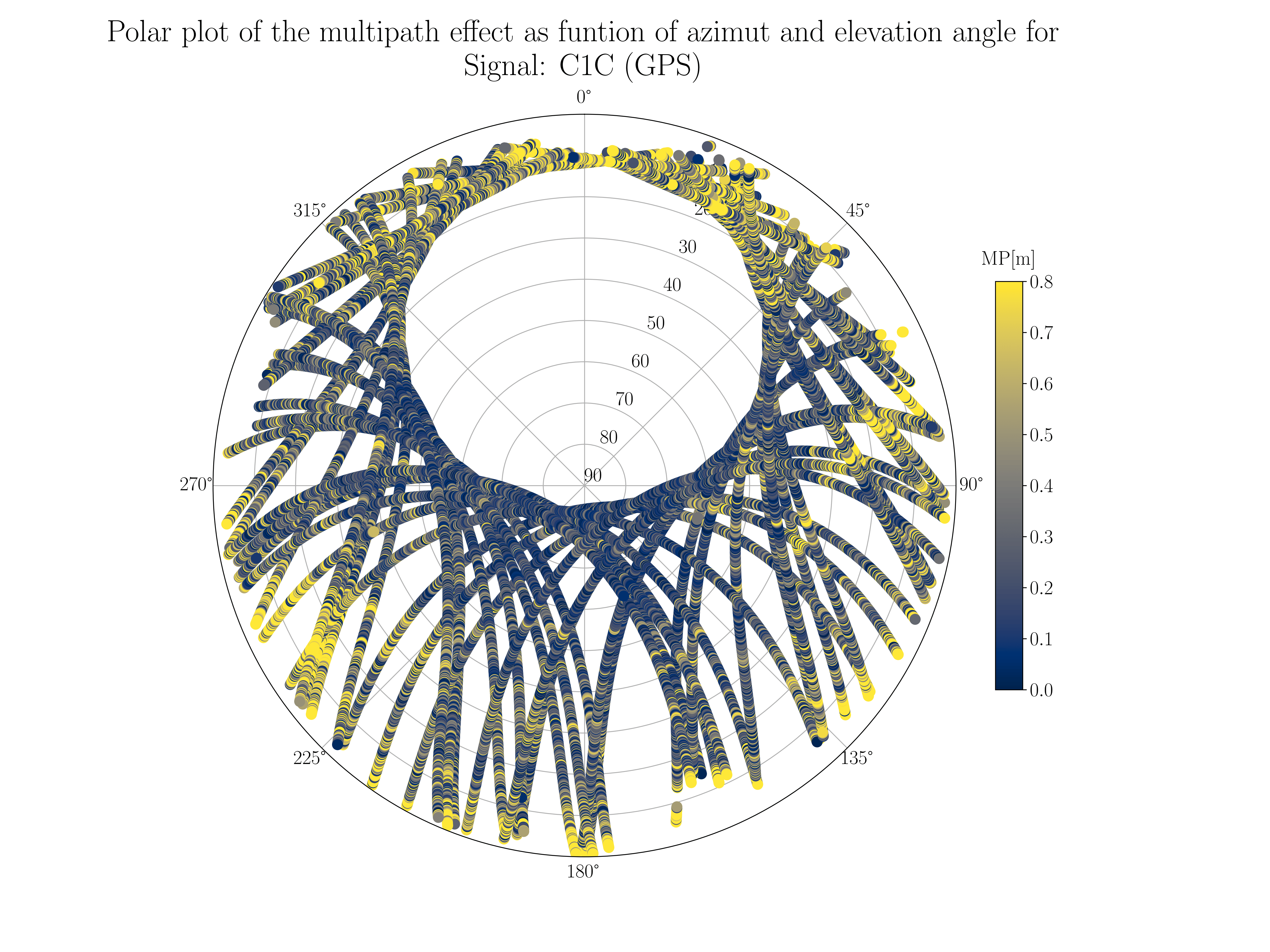
  • Polar plot of each observed satellite in the system

    

  • Signal-To-Noise Ratio (SNR) plotted wrt time and elevation angle (combine)

    

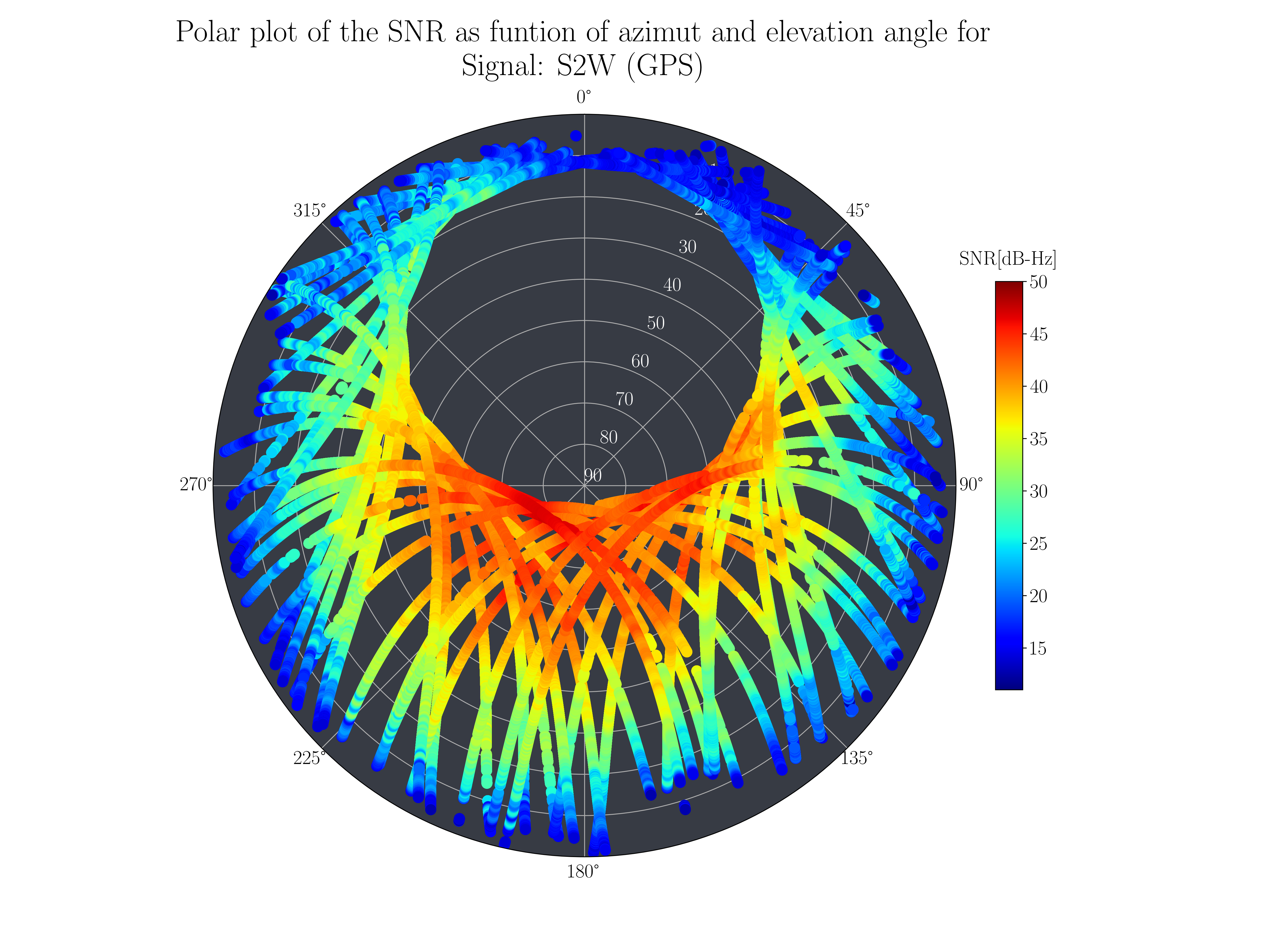
  • Polar plot of Signal-To-Noise Ratio (SNR)

    

• Exporting the results as a pickle file which easily can be imported into python as a dictionary
• The results in form of a report get written to a text file with the same name as the RINEX observation file.
• The estimated values are also written to a CSV file by default

  

User arguments

The GNSS_MultipathAnalysis function accepts several keyword arguments that allow for detailed customization of the analysis process. Below is a list of the first five arguments:

• rinObsFilename (str): Path to the RINEX 3 observation file. This is a required argument.

• broadcastNav1 (Union[str, None], optional): Path to the first RINEX navigation file. Default is None.

• broadcastNav2 (Union[str, None], optional): Path to the second RINEX navigation file (if available). Default is None.

• broadcastNav3 (Union[str, None], optional): Path to the third RINEX navigation file (if available). Default is None.

• broadcastNav4 (Union[str, None], optional): Path to the fourth RINEX navigation file (if available). Default is None.

More...

• sp3NavFilename_1 (Union[str, None], optional): Path to the first SP3 navigation file. Default is None.

• sp3NavFilename_2 (Union[str, None], optional): Path to the second SP3 navigation file (optional). Default is None.

• sp3NavFilename_3 (Union[str, None], optional): Path to the third SP3 navigation file (optional). Default is None.

• desiredGNSSsystems (Union[List[str], None], optional): List of GNSS systems to include in the analysis. For example, ['G', 'R'] to include only GPS and GLONASS. Default is all systems (None).

• phaseCodeLimit (Union[float, int, None], optional): Critical limit that indicates cycle slip for phase-code combination in m/s. If set to 0, the default value of 6.667 m/s will be used. Default is None.

• ionLimit (Union[float, None], optional): Critical limit indicating cycle slip for the rate of change of the ionospheric delay in m/s. If set to 0, the default value of 0.0667 m/s will be used. Default is None.

• cutoff_elevation_angle (Union[int, None], optional): Cutoff angle for satellite elevation in degrees. Estimates with elevation angles below this value will be excluded. Default is None.

• outputDir (Union[str, None], optional): Path to the directory where output files should be saved. If not specified, the output will be generated in a sub-directory within the current working directory. Default is None.

• plotEstimates (bool, optional): Whether to plot the estimates. Default is True.

• plot_polarplot (bool, optional): Whether to generate polar plots. Default is True.

• include_SNR (bool, optional): If set to True, the Signal-to-Noise Ratio (SNR) from the RINEX observation file will be included in the analysis. Default is True.

• save_results_as_pickle (bool, optional): If True, the results will be saved as a binary pickle file. Default is True.

• save_results_as_compressed_pickle (bool, optional): If True, the results will be saved as a binary compressed pickle file using zstd compression. Default is False.

• write_results_to_csv (bool, optional): If True, a subset of the results will be exported as a CSV file. Default is True.

• output_csv_delimiter (str, optional): The delimiter to use for the CSV file. Default is a semicolon (;).

• nav_data_rate (int, optional): The desired data rate for ephemerides in minutes. A higher value speeds up processing but may reduce accuracy. Default is 60 minutes.

• includeResultSummary (Union[bool, None], optional): Whether to include a detailed summary of statistics in the output file, including for individual satellites. Default is None.

• includeCompactSummary (Union[bool, None], optional): Whether to include a compact overview of statistics in the output file. Default is None.

• includeObservationOverview (Union[bool, None], optional): Whether to include an overview of observation types for each satellite in the output file. Default is None.

• includeLLIOverview (Union[bool, None], optional): Whether to include an overview of LLI (Loss of Lock Indicator) data in the output file. Default is None.

• use_LaTex (bool, optional): If True, LaTeX will be used for rendering text in plots, requiring LaTeX to be installed on your system. Default is True.

Output

• analysisResults (dict): A dictionary containing the results of the analysis for all GNSS systems.

Compatibility

• Python Versions: Compatible with Python 3.8 and above.
• Dependencies: All dependencies will be automatically installed with pip install gnssmultipath.

License

This project is licensed under the MIT License - see the LICENSE file for details.

Some simple examples on how to use the software:

Run a multipath analysis using a SP3 file and only mandatory arguments

from gnssmultipath import GNSS_MultipathAnalysis

rinObs_file = 'OPEC00NOR_S_20220010000_01D_30S_MO_3.04'
SP3_file    = 'SP3_20220010000.eph'
analysisResults = GNSS_MultipathAnalysis(rinex_obs_file=rinObs_file, sp3NavFilename_1=SP3_file)

Run a multipath analysis using a RINEX navigation file with SNR, a defined datarate for ephemerides and with an elevation angle cut off at 10°

from gnssmultipath import GNSS_MultipathAnalysis

# Input arguments
rinObs_file = 'OPEC00NOR_S_20220010000_01D_30S_MO_3.04'
rinNav_file = 'BRDC00IGS_R_20220010000_01D_MN.rnx'
output_folder = 'C:/Users/xxxx/Results_Multipath'
cutoff_elevation_angle = 10  # drop satellites lower than 10 degrees
nav_data_rate = 60  # desired datarate for ephemerides (to improve speed)

analysisResults = GNSS_MultipathAnalysis(rinex_obs_file=rinObs_file,
                                         broadcastNav1=rinNav_file,
                                         include_SNR=True,
                                         outputDir=output_folder,
                                         nav_data_rate=nav_data_rate,
                                         cutoff_elevation_angle=cutoff_elevation_angle)

Run analysis with several navigation files

from gnssmultipath import GNSS_MultipathAnalysis

outputdir = 'path_to_your_output_dir'
rinObs = "OPEC00NOR_S_20220010000_01D_30S_MO_3.04_croped.rnx"

# Define the path to your RINEX navigation file
rinNav1 = "OPEC00NOR_S_20220010000_01D_CN.rnx"
rinNav2 = "OPEC00NOR_S_20220010000_01D_EN.rnx"
rinNav3 = "OPEC00NOR_S_20220010000_01D_GN.rnx"
rinNav4 = "OPEC00NOR_S_20220010000_01D_RN.rnx"

analysisResults = GNSS_MultipathAnalysis(rinObs,
                                         broadcastNav1=rinNav1,
                                         broadcastNav2=rinNav2,
                                         broadcastNav3=rinNav3,
                                         broadcastNav4=rinNav4,
                                         outputDir=outputdir)

Run analysis without making plots

from gnssmultipath import GNSS_MultipathAnalysis

rinObs_file = 'OPEC00NOR_S_20220010000_01D_30S_MO_3.04'
SP3_file    = 'SP3_20220010000.eph'
analysisResults = GNSS_MultipathAnalysis(rinex_obs_file=rinObs_file, sp3NavFilename_1=SP3_file, plotEstimates=False)

Run analysis and use the Zstandard compression algorithm (ZSTD) to compress the pickle file storing the results

from gnssmultipath import GNSS_MultipathAnalysis

rinObs_file = 'OPEC00NOR_S_20220010000_01D_30S_MO_3.04'
SP3_file    = 'SP3_20220010000.eph'
analysisResults = GNSS_MultipathAnalysis(rinex_obs_file=rinObs_file, sp3NavFilename_1=SP3_file, save_results_as_compressed_pickle=True)

Read a RINEX observation file

from gnssmultipath import readRinexObs

rinObs_file = 'OPEC00NOR_S_20220010000_01D_30S_MO_3.04'
GNSS_obs, GNSS_LLI, GNSS_SS, GNSS_SVs, time_epochs, nepochs, GNSSsystems, \
        obsCodes, approxPosition, max_sat, tInterval, markerName, rinexVersion, recType, timeSystem, leapSec, gnssType, \
        rinexProgr, rinexDate, antDelta, tFirstObs, tLastObs, clockOffsetsON, GLO_Slot2ChannelMap, success = \
        readRinexObs(rinObs_file)

Read a RINEX navigation file (v.3)

from gnssmultipath import Rinex_v3_Reader

rinNav_file = 'BRDC00IGS_R_20220010000_01D_MN.rnx'
navdata = Rinex_v3_Reader().read_rinex_nav(rinNav_file, data_rate=60)

Read in the results from an uncompressed Pickle file

from gnssmultipath import PickleHandler

path_to_picklefile = 'analysisResults.pkl'
result_dict = PickleHandler.read_pickle(path_to_picklefile)

Read in the results from a compressed Pickle file

from gnssmultipath import PickleHandler

path_to_picklefile = 'analysisResults.pkl'
result_dict = PickleHandler.read_zstd_pickle(path_to_picklefile)

Estimate the receiver position based on pseudoranges using SP3 file and print the standard deviation of the estimated position

from gnssmultipath import GNSSPositionEstimator
import numpy as np

rinObs = 'OPEC00NOR_S_20220010000_01D_30S_MO_3.04_croped.rnx'
sp3 = 'Testfile_20220101.eph'

# Set desired time for when to estimate position and which system to use
desired_time = np.array([2022, 1, 1, 1, 5, 30.0000000])
desired_system = "G"  # GPS
gnsspos, stats = GNSSPositionEstimator(rinObs,
                                    sp3_file = sp3,
                                    desired_time = desired_time,
                                    desired_system = desired_system,
                                    elevation_cut_off_angle = 15
                                    ).estimate_position()

print('Estimated coordinates in ECEF (m):\n' + '\n'.join([f'{axis} = {coord}' for axis, coord in zip(['X', 'Y', 'Z'], np.round(gnsspos[:-1], 3))]))
print('\nStandard deviation of the estimated coordinates (m):\n' + '\n'.join([f'{k} = {v}' for k, v in stats["Standard Deviations"].items() if k in ['Sx', 'Sy', 'Sz']]))

Estimate the receiver position based on pseudoranges using RINEX navigation file and print the DOP values

from gnssmultipath import GNSSPositionEstimator
import numpy as np

rinObs = 'OPEC00NOR_S_20220010000_01D_30S_MO_3.04_croped.rnx'
rinNav = 'BRDC00IGS_R_20220010000_01D_MN.rnx'

# Set desired time for when to estimate position and which system to use
desired_time = np.array([2022, 1, 1, 2, 40, 0.0000000])
desired_system = "R"  # GLONASS


gnsspos, stats = GNSSPositionEstimator(rinObs,
                                    rinex_nav_file = rinNav,
                                    desired_time = desired_time,
                                    desired_system = desired_system,
                                    elevation_cut_off_angle = 10).estimate_position()

print('Estimated coordinates in ECEF (m):\n' + '\n'.join([f'{axis} = {coord}' for axis, coord in zip(['X', 'Y', 'Z'], np.round(gnsspos[:-1], 3))]))
print('\nStandard deviation of the estimated coordinates (m):\n' + '\n'.join([f'{k} = {v}' for k, v in stats["Standard Deviations"].items() if k in ['Sx', 'Sy', 'Sz']]))
print(f'\nDOP values:\n' + '\n'.join([f'{k} = {v}' for k, v in stats["DOPs"].items()]))

Estimate the receiver's position based on pseudoranges in the desired CRS

Define a specific Coordinate Reference System (CRS) to output the estimated receiver's coordinates. In this case the coordinates will be given in WGS84 UTM zone 32N (EPSG:32632) and ellipsoidal heights.

Note: You can use the EPSG GeoRepository to find the EPSG code for the desired CRS.

from gnssmultipath import GNSSPositionEstimator
import numpy as np


rinObs = 'OPEC00NOR_S_20220010000_01D_30S_MO_3.04_croped.rnx'
rinNav = 'BRDC00IGS_R_20220010000_01D_MN.rnx'

# Set desired time for when to estimate position and which system to use
desired_time = np.array([2022, 1, 1, 1, 5, 30.0000000])
desired_system = "E"  # GPS
desired_crs = "EPSG:32632"  # Desired CRS for the estimated receiver coordinates (WGS84 UTM zone 32N)
gnsspos, stats = GNSSPositionEstimator(rinObs,
                                    rinex_nav_file=rinNav,
                                    desired_time = desired_time,
                                    desired_system = desired_system,
                                    elevation_cut_off_angle = 10,
                                    crs=desired_crs).estimate_position()

print('Estimated coordinates in ECEF (m):\n' + '\n'.join([f'{axis} = {coord}' for axis, coord in zip(['Eastin', 'Northing', 'Height (ellipoidal)'], np.round(gnsspos[:-1], 3))]))

Some background information on implementation

Converting Keplerian Elements to ECEF Coordinates

This section explains step-by-step how satellite positions in Keplerian elements are converted to Earth-Centered Earth-Fixed (ECEF) coordinates. The explanation is showing how the kepler2ecef method has implemented this conversion. This approch works for GPS, Galileo and BeiDou, but not for GLONASS. GLONASS is not storing the satellite positions as Keplerian elements, but uses a state vector instead. The coordinates then get interpolated to the current epoch by solving the differential equation using a 4th order Runge-Kutta.

Steps for Conversion

1. Constants and Inputs

• Gravitational Constant and Earth's Mass ($GM$):

$$ GM = 3.986005 \times 10^{14} , \text{m}^3/\text{s}^2 $$

• Earth's Angular Velocity ($\omega_e $):

$$ \omega_e = 7.2921151467 \times 10^{-5} , \text{rad/s} $$

• Speed of Light ($c$):

$$ c = 299792458 , \text{m/s} $$

Inputs:

• Keplerian elements from the RINEX navigation file.
• Receiver's ECEF coordinates $(x_\text{rec}, y_\text{rec}, z_\text{rec})$.

2. Calculate Orbital Parameters

Mean Motion ($n_0$):

$$ n_0 = \sqrt{\frac{GM}{A^3}} $$

where $A = a^2 (\text{semimajor axis})$.

Corrected Mean Motion ($n_k$):

$$ n_k = n_0 + \Delta n $$

Time Since Reference Epoch ($t_k$):

$$ t_k = \text{TOW}_\text{rec} - \text{TOE} $$

Mean Anomaly ($M_k$):

$$ M_k = M_0 + n_k t_k $$

where $M_0$ is the mean anomaly at reference epoch.

3. Solve for Eccentric Anomaly ($E$):

Use iterative approximation to solve Kepler's equation:

$$ E = M_k + e \sin(E) $$

Repeat until convergence, where:

$$ |E_{\text{new}} - E_{\text{old}}| < \epsilon $$

where $\epsilon$ could be set to $1e-12$

4. Calculate True Anomaly ($\nu$):

Compute $\cos(\nu)$ and $\sin(\nu)$:

$$ \cos(\nu) = \frac{\cos(E) - e}{1 - e \cos(E)}, \quad \sin(\nu) = \frac{\sqrt{1 - e^2} \sin(E)}{1 - e \cos(E)} $$

Use the arctangent to find $\nu$:

$$ \nu = \arctan2(\sin(\nu), \cos(\nu)) $$

5. Compute Orbital Corrections

Corrected Argument of Latitude ($u_k$):

$$ u_k = \nu + \omega + C_{uc} \cos(2u) + C_{us} \sin(2u) $$

Corrected Radius ($r_k$):

$$ r_k = A (1 - e \cos(E)) + C_{rc} \cos(2u) + C_{rs} \sin(2u) $$

Corrected Inclination ($i_k$):

$$ i_k = i_0 + i_\text{dot} t_k + C_{ic} \cos(2u) + C_{is} \sin(2u) $$

6. Longitude of Ascending Node

Account for Earth's rotation:

$$ \Omega_k = \Omega_0 + (\dot{\Omega} - \omega_e)t_k - \omega_e \text{TOE} $$

7. Satellite Position in Orbital Plane

$x$ and $y$ in the orbital plane:

$$ \begin{align*} x &= r_k \cos(u_k) \ y &= r_k \sin(u_k) \end{align*} $$

8. Transform to ECEF Coordinates

Convert from the orbital frame to the Earth-centered, Earth-fixed frame:

$$ \begin{gather*} X = x \cos(\Omega_k) - y \sin(\Omega_k) \cos(i_k) \ Y = x \sin(\Omega_k) + y \cos(\Omega_k) \cos(i_k) \ Z = y \sin(i_k) \end{gather*} $$

9. Relativistic Clock Correction

Account for relativistic effects:

$$ \Delta T_\text{rel} = -\frac{2 \sqrt{A \cdot GM}}{c^2} e \sin(E) $$

10. Earth Rotation Correction (Sagnac Effect)

If the receiver position is known, adjust for the Earth's rotation during signal transmission using an iterative process to correct for the Sagnac effect. The Sagnac effect accounts for the Earth's rotation during the signal's travel time from the satellite to the receiver. This correction ensures that the satellite's position aligns with the time of signal transmission, adjusting for the Earth's rotation.

The Earth's rotation during the signal's travel introduces a positional error if uncorrected. This adjustment ensures high-accuracy satellite positioning and is implemented in the kepler2ecef method part of the Kepler2ECEF class, and the iterative method ensures precise compensation for the Earth's rotation during signal travel time.

Iterative Algorithm for Earth Rotation Correction

Initialize Variables:

• $\text{TRANS}_0$: Approximate initial signal travel time, e.g., 0.075 seconds.
• $\text{TRANS}$: Variable to store updated travel time.
• $j$: Iteration counter.

Iterative Process:

Update the longitude of the ascending node ($\Omega_k$) to account for the Earth's rotation during the signal travel time:

$$ \begin{equation*} \Omega_k = \Omega_0 + (\dot{\Omega} - \omega_e)t_k - \omega_e(\text{TOE} + \text{TRANS}) \end{equation*} $$

Recalculate ECEF coordinates:

$$ \begin{gather*} X = x \cos(\Omega_k) - y \sin(\Omega_k) \cos(i_k) \ Y = x \sin(\Omega_k) + y \cos(\Omega_k) \cos(i_k) \ Z = y \sin(i_k) \end{gather*} $$

Compute the distance ($\text{DS}$) between the satellite and the receiver:

$$ \text{DS} = \sqrt{(X - x_\text{rec})^2 + (Y - y_\text{rec})^2 + (Z - z_\text{rec})^2} $$

Update the travel time:

$$ \text{TRANS}_0 = \frac{\text{DS}}{c} $$

Convergence:

Repeat the process until:

$$ |\text{TRANS}_0 - \text{TRANS}| < \epsilon $$

Where $\epsilon$ is a small threshold, e.g., $10^{-10}$. Once the iteration converges, the corrected ECEF coordinates are $X, Y, Z$ and the relativistic clock correction $\Delta T_\text{rel}$.

Interpolating a GLONASS State Vector to ECEF Coordinates

This section explains the steps taken to interpolate GLONASS state vectors using the 4th-order Runge-Kutta method, based on the interpolate_glonass_coord_runge_kutta function provided. The 4th-order Runge-Kutta method is a numerical technique to approximate the solution of ordinary differential equations (ODEs). It iteratively updates the state vector based on the derivatives computed at intermediate steps.

The GLONASS equations of motion describe how the satellite's state (position and velocity) evolves over time under the influence of gravitational and perturbative forces. These equations are differential equations, as they involve derivatives of the satellite's position and velocity.

The state vector $\text{state} = [x, y, z, v_x, v_y, v_z]$ includes the satellite's position ($x, y, z$) and velocity ($v_x, v_y, v_z$). The derivatives of the state vector represent the equations of motion for the GLONASS satellite which include:

Change in Position

$$ \dot{x}, \dot{y}, \dot{z} $$

which equals the velocity components

$$ v_x, v_y, v_z s$$

Change in Velocity

$$ \dot{v_x}, \dot{v_y}, \dot{v_z} $$

depends on:

• Gravitational forces.
• Perturbations (e.g., due to Earth's oblateness).
• External accelerations ($J_x, J_y, J_z$).

1. Inputs

• Ephemerides Data: Broadcast ephemerides, including position, velocity, acceleration, and clock corrections, from a RINEX navigation file.
• Observation Epochs: Array of observation times, given as GPS week and time of week (TOW).

2. Extract and Convert Ephemeris Data

• Read ephemerides parameters for the GLONASS satellite:
  • $x_e, y_e, z_e$: Satellite positions at reference time $t_e$ (PZ-90) [km].
  • $v_x, v_y, v_z$: Satellite velocities at $t_e$ [km/s].
  • $J_x, J_y, J_z$: Acceleration components at $t_e$ $[km/s^2]$.
  • $\tau_N$: Clock bias [s].
  • $\gamma_N$: Clock frequency bias.

Positions, velocities, and accelerations are converted from kilometers to meters.

3. Time Difference ($\Delta t$)

Convert the reference time $t_e$ from UTC to GPST by adding leap seconds:

$$ t_\text{GPST} = t_e + \text{leap seconds} $$

Compute the time difference between observation and reference epochs:

$$ \Delta t= t_\text{obs} - t_\text{GPST} $$

4. Clock Corrections

Satellite clock error:

$$ \text{clock error} = \tau_N + \Delta t\cdot \gamma_N $$

Clock rate error:

$$ \text{clock rate error} = \gamma_N $$

5. Initialize State Vector

Initial state vector:

$$ state_{vec} = \begin{bmatrix} x_e \ y_e \ z_e \ v_x \ v_y \ v_z \end{bmatrix} $$

Initial acceleration vector:

$$ a_{vec} = \begin{bmatrix} J_x \ J_y \ J_z \end{bmatrix} $$

6. Runge-Kutta Integration

• Time step ($t_\text{step}$): 90 seconds, adjusted based on the magnitude of $\Delta t$.
• Iterate using the 4th-order Runge-Kutta method until $\Delta t$ is less than a small threshold (e.g., $10^{-9}$).

Runge-Kutta Equations:

Solving the system of ordinary differential equations (ODEs) using the 4th-order Runge-Kutta method. Runge-Kutta interpolation method implemented in the glonass_diff_eq method apart of the GLOStateVec2ECEF class.

derivatives = glonass_diff_eq(state_vec, a_vec)

this method will be refered to as $f$ from now.

Runge-Kutta steps

Calculate Derivatives: Compute the derivatives using the current state vector and acceleration:

$$ k_1 = f(state_{vec_n}, a_{vec}) $$

$$ k_2 = f\left(state_{vec_n} + \frac{k_1 \cdot t_{step}}{2}, a_{vec} \right) $$

$$ k_3 = f\left(state_{vec_n} + \frac{k_2 \cdot t_{step}}{2}, a_{vec} \right) $$

$$ k_4 = f\left(state_{vec_n} + k_3 \cdot t_{step}, a_{vec} \right) $$

Update State Vector: Compute the updated state vector ($state_{vec_{n+1}}$) as:

$$ state_{vec_{n+1}} = state_{vec_n} + \frac{1}{6} (k_1 + 2k_2 + 2k_3 + k_4) \cdot t_{step} $$

Update Time: Increment the time to the next step:

$$ t_{n+1} = t_n + t_\text{step} $$

Reduce$\Delta t$: Adjust the remaining time difference:

$$ \Delta t = \Delta t - t_\text{step} $$

7. Final Outputs

• Position ($x, y, z$) [m]: Extracted from the final state vector.
• Velocity ($v_x, v_y, v_z$) [m/s]: Extracted from the final state vector.
• Clock Error ($\text{clock error}$) [s]: Calculated during initialization.
• Clock Rate Error ($\text{clock rate error}$) [s/s]: Calculated during initialization.

GLONASS Equations of Motion

The derivatives of the state vector ($x, y, z, v_x, v_y, v_z$) are computed as follows:

Radial Distance ($r$):

$$ r = \sqrt{x^2 + y^2 + z^2} $$

Acceleration Terms: Gravitational acceleration:

$$ a_\text{grav} = -\frac{\mu}{r^3} $$

Perturbation due to Earth's oblateness ($J_2$):

$$ a_\text{J2} = 1.5 J_2 \frac{\mu a_e^2}{r^5} \left( 1 - 5 \frac{z^2}{r^2} \right) $$

• Equations of Motion:

$$ \dot{x} = v_x, \quad \dot{y} = v_y, \quad \dot{z} = v_z $$

$$ \dot{v_x} = a_\text{grav} x + a_\text{J2} x + 2\omega v_y + \omega^2 x + J_x $$

$$ \dot{v_y} = a_\text{grav} y + a_\text{J2} y - 2\omega v_x + \omega^2 y + J_y $$

$$ \dot{v_z} = a_\text{grav} z + a_\text{J2} z + J_z $$

where:

• $\mu = 3.9860044 \times 10^{14}$ $[m^3/s^2]$ is the gravitational constant.
• $J_2 = 1.0826257 \times 10^{-3}$ is the Earth's oblateness factor.
• $\omega = 7.292115 \times 10^{-5}$ $[rad/s]$ is the Earth's rotation rate.
• $a_e = 6378136.0$ $[m]$ is the semi-major axis of the Earth (PZ-90 ellipsoid).

This method ensures precise interpolation of GLONASS satellite positions and velocities at user-specified epochs.

Interpolating Precise Satellite Coordinates from SP3 file Using Neville's Algorithm

This section explains the steps taken by the SP3Interpolator Python class to compute precise satellite positions from SP3 files. The method leverages Neville's algorithm to perform polynomial interpolation for satellite positions $(X, Y, Z)$ and clock biases at user-specified epochs. The SP3 file is read by the SP3Reader class.

1. Input Data

• SP3 Data: Satellite positions $(X_i, Y_i, Z_i)$ and clock biases $\text{Bias}_i$ are provided at discrete epochs $\text{Epoch}_i$. They are extracted from the SP3 file, and the units of the coordiantes are converted from kilometers to meters. The clock bias is converted from microseconds to seconds.
• Target Epoch: The observation times ($t$) where interpolation is required. The target epoch is typically the obervation time/epochs from the RINEX observation file.

2. Select Nearest Points

For a given target time $t$:

• Compute the time difference:

$$ \Delta t_i = |\text{Epoch}_i - t| $$

Here, $\text{Epoch}_i$ is the time of the $i$-th SP3 entry in seconds. 2. Select the $n$ nearest epochs around the given target time $t$ (e.g., $n=7$) by sorting $\Delta t_i$ in ascending order. By default the number of nearest points for interpolation is set to 7.

3. Apply Neville's Algorithm

Neville's algorithm computes the interpolated value $P(t)$ using $n$ known points $(x_i, y_i)$, where:

• $x_i = \text{Epoch}_i$
• $p_{i,0}$ is initialized with the satellite data, such as $X_i$, $Y_i$, $Z_i$, or $\text{Bias}_i$.

Recursive Formula

The recursive interpolation formula is:

$$ p_{i,j}(t) = \frac{ (t - x_i) \cdot p_{i+1,j-1}(t) - (t - x_{i+j}) \cdot p_{i,j-1}(t) }{ x_{i+j} - x_i } $$

Where:

• $p_{i,0}(t) = y_i$ (initial values) and $j$ is the current degree of the interpolating polynomial.
• $t$ represents the target value or interpolation point at which the function $P(t)$ is being approximated.
  • In the context of satellite interpolation $t$ is the target epoch or the observation time (in seconds since the reference epoch) for which you are interpolating satellite positions or clock biases. $t$ falls between the nearest known SP3 epochs, $x_i$, and is used for interpolation. $t$ determines the relative weights of the contributions from the known data points $(x_i, y_i)$ to the final interpolated value. For example if you're interpolating the $X$-coordinate of a satellite, $t$ is the observation time at which you want to know the satellite's $X$-position. The algorithm uses $t$ to calculate how much influence each known SP3 epoch $x_i$ and corresponding $y_i$ (satellite's $X$-position at $x_i$) has on the result.
• Index $i$ represents the starting point of the interval in the dataset. For example, $p_{i,j}$ corresponds to the interpolated value using points starting from $x_i$.
• Index $j$ represents the degree of the polynomial being calculated. $j=0$ corresponds to the initial dataset values ($p_{i,0} = y_i$), while $j=n-1$ represents the final interpolated polynomial.

Algorithm Implementation

• Begin with $p_{i,0} = y_i$.
• Compute higher-degree polynomials:

$$ p_{i,j}(t) \quad \text{for} \quad j = 1, 2, \dots, n-1. $$

• After completing $j = n-1$, the interpolated value is $P(t) = p_{0,n-1}(t)$.

4. Repeat for Each Coordinate component and for the satellite clock bias

Repeat the above steps independently for $X$, $Y$, $Z$, and the clock bias, resulting in $(X, Y, Z, \text{Bias}) \quad \text{at time } t$

Mathematical Summary

Given $n$ nearest points: Let:

$$ p_{i,j}(t) = \begin{cases} y_i & \text{if } j = 0 \ \frac{ (t - x_i) p_{i+1,j-1} - (t - x_{i+j}) p_{i,j-1} }{ x_{i+j} - x_i } & \text{if } j > 0 \end{cases} $$

The interpolated value is:

$$ P(t) = p_{0,n-1}(t). $$

Example code outlining how Neville's algorithm can be implemented (dummy data)

Click to expand the code

import numpy as np

def interpolate_satellite_data(observation_time, nearest_times, nearest_positions, nearest_clock_biases):
    """
    Interpolates satellite positions and clock bias for a single observation time using Neville's algorithm.

    Parameter:
    ----------
    observation_time : float. Target epoch in seconds (time for which interpolation is required).
    nearest_times : np.ndarray. Array of closest times (epochs) from the SP3 file.
    nearest_positions : np.ndarray. Array of closest satellite positions (X, Y, Z) from the SP3 file.
    nearest_clock_biases : np.ndarray. Array of closest clock biases from the SP3 file.

    Returns:
    -------
    interpolated_position : np.ndarray. Interpolated satellite position (X, Y, Z) at the target epoch.
    interpolated_clock_bias : float. Interpolated clock bias at the target epoch.
    """
    def neville_interpolate(x, y, n):
        """
        Perform polynomial interpolation using Neville's algorithm.

        Parameters:
        ----------
        x : np.ndarray. Differences between nearest times and the target time.
        y : np.ndarray. Satellite data to interpolate (positions or biases).
        n : int. Number of data points.

        Returns:
        -------
        Interpolated value (float)
        """
        y_copy = y.copy()
        for j in range(1, n):
            for i in range(n - j):
                y_copy[i] = ((x[i + j] * y_copy[i] - x[i] * y_copy[i + 1]) / (x[i + j] - x[i]))
        return y_copy[0]

    # Compute time differences relative to the target epoch
    time_diff = nearest_times - observation_time

    # Interpolate satellite positions (X, Y, Z)
    interpolated_position = np.zeros(3)
    for i in range(3):  # Loop over X, Y, Z
        interpolated_position[i] = neville_interpolate(time_diff, nearest_positions[:, i], len(nearest_times))

    # Interpolate clock bias
    interpolated_clock_bias = neville_interpolate(time_diff, nearest_clock_biases, len(nearest_times))

    return interpolated_position, interpolated_clock_bias




if __name__ == "__main__":
	# Example usage on dummy data
	observation_time = 100000  # Example observation time in seconds
	nearest_times = np.array([99990, 99995, 100000, 100005, 100010])  # Example nearest times
	nearest_positions = np.array([
		[1000, 2000, 3000],  # Example X, Y, Z positions
		[1010, 2010, 3010],
		[1020, 2020, 3020],
		[1030, 2030, 3030],
		[1040, 2040, 3040]
	])
	nearest_clock_biases = np.array([0.0005, 0.0006, 0.0007, 0.00008, 0.00009])  # Example clock biases

	interpolated_position, interpolated_clock_bias = interpolate_satellite_data(
		observation_time, nearest_times, nearest_positions, nearest_clock_biases
	)

	print("Interpolated Position (X, Y, Z):", interpolated_position)
	print("Interpolated Clock Bias:", interpolated_clock_bias)

Estimating the Receiver Position Using Least Squares

This section describes how the software estimates the approximate receiver position using pseudoranges and satellite positions through an iterative least-squares adjustment.

Steps for Estimation

1. Inputs

• Satellite Positions: The satellite coordinates $(X, Y, Z)$ in ECEF coordinates.
• Pseudoranges ($R_{ji}$): The measured distance between the receiver and satellites, corrected for clock errors and relativistic effects.
• Initial Receiver Position ($x, y, z$): An approximate starting position for the receiver in ECEF coordinates. Can be set to $(0, 0, 0)$ initially.
• Clock Bias ($dT_0$): An initial estimate of the receiver's clock bias.

2. Compute Geometric Range ($\rho$)

For each satellite, compute the geometric distance between the receiver and the satellite:

$$ \rho = \sqrt{(X - x)^2 + (Y - y)^2 + (Z - z)^2} $$

3. Linearization via Taylor Series and Construction of the Design Matrix ($A$)

The observation equation for pseudoranges is non-linear. Before we can use linear algebra, we need to linearize it using a first-order Taylor series expansion. This linearization assumes small corrections to the initial approximate values of $(x,y,z,dT)$. The pseudorange equation is:

$$ R_{ji} = \sqrt{(X - x)^2 + (Y - y)^2 + (Z - z)^2} + dT $$

where $(X, Y, Z)$ are satellite coordinates, $(x, y, z)$ are receiver coordinates and $dT$ is the clock bias. The equation is linearized around an initial guess $(x_0, y_0, z_0, dT_0)$. Using a first-order Taylor series expansion, we get:

$$ R_{ji} \approx R_{ji,0} + \frac{\partial R_{ji}}{\partial x} \Delta x + \frac{\partial R_{ji}}{\partial y} \Delta y + \frac{\partial R_{ji}}{\partial z} \Delta z + \frac{\partial R_{ji}}{\partial dT} \Delta dT $$

where $R_{ji,0}$ is the pseudorange computed at the initial guess. $\Delta x, \Delta y, \Delta z, \Delta dT$ are the corrections to the initial guess. The partial derivatives become:

$$ \frac{\partial R_{ji}}{\partial x} = -\frac{X - x}{\rho}, \quad \frac{\partial R_{ji}}{\partial y} = -\frac{Y - y}{\rho}, \quad \frac{\partial R_{ji}}{\partial z} = -\frac{Z - z}{\rho}, \quad \frac{\partial R_{ji}}{\partial dT} = 1 $$

The design matrix $A$ is constructed using these derivatives:

$$ A = \begin{bmatrix} -\frac{X_1 - x}{\rho_1} & -\frac{Y_1 - y}{\rho_1} & -\frac{Z_1 - z}{\rho_1} & 1 \ -\frac{X_2 - x}{\rho_2} & -\frac{Y_2 - y}{\rho_2} & -\frac{Z_2 - z}{\rho_2} & 1 \ \vdots & \vdots & \vdots & \vdots \ -\frac{X_n - x}{\rho_n} & -\frac{Y_n - y}{\rho_n} & -\frac{Z_n - z}{\rho_n} & 1 \end{bmatrix} $$

This linearized system is solved iteratively, updating $(x, y, z, dT)$ until convergence.

4. Observation Vector ($l$)

The observation vector $l$ represents the difference between the measured pseudoranges and the calculated distances:

$$ l = R_{ji} + c \cdot dT_\text{rel} - (\rho + c \cdot dT_i) $$

5. Normal Matrix ($N$)

The normal matrix is computed as:

$$ N = A^T A $$

6. Correction Vector ($h$)

The correction vector is computed as:

$$ h = A^T l $$

7. Solve for Updates ($\Delta x, \Delta y, \Delta z, \Delta dT_0$)

Solve the linear system:

$$ \Delta \mathbf{x} = N^{-1} h $$

where $\Delta \mathbf{x} = [\Delta x, \Delta y, \Delta z, \Delta dT_0]^T$.

8. Update Receiver Position

Update the receiver's position and clock bias:

$$ x \gets x + \Delta x $$

$$ y \gets y + \Delta y $$

$$ z \gets z + \Delta z $$

$$ dT_0 \gets dT_0 + \frac{\Delta dT_0}{c} $$

9. Iteration

Repeat steps 2–8 until the largest correction in $\Delta \mathbf{x}$ is smaller than a given tolerance ($1 \times 10^{-8}$), or the maximum number of iterations is reached.

Iteration Process in Detail

Initialization: - Start with approximate receiver position $(x, y, z)$ and clock bias $dT_0 = 0$. - Set the improvement threshold and maximum number of iterations.

Convergence Check:

• After each iteration, compute the improvement:

$$ \text{improvement} = \max(|\Delta x|, |\Delta y|, |\Delta z|, |\Delta dT_0|) $$

• If the improvement is below the threshold, stop the iteration.

Satellite Filtering:

• After convergence, filter out satellites with low elevation angles (e.g., $< 15^\circ$).
• Recompute the receiver position using the remaining satellites.

Final Outputs

• Receiver Position ($x, y, z$): The estimated ECEF coordinates of the receiver.
• Clock Bias ($dT_i$): The estimated receiver clock bias in seconds.
• Statistical Analysis: Includes residuals, variances, and diagnostics for the least-squares solution.

This iterative least-squares approach ensures high accuracy in estimating the receiver's position while accounting for satellite clock errors and relativistic corrections.

Statistical Parameters of the estimated position

This section describes the key statistical parameters computed during the GNSS positioning process, their significance, and how they are calculated.

1. Residuals ($V$)

Residuals represent the differences between observed and computed values:

$$ V = A \cdot h - l $$

where $A$ is the Design matrix, $h$ is the Adjustments vector and $l$ is the Observations vector. Significance: Residuals indicate the quality of the fit between the observed pseudoranges and the model.

2. Sum of Squared Errors (SSE)

The SSE quantifies the total error in the fit:

$$ \text{SSE} = V^T \cdot V $$

Significance: A smaller SSE indicates a better fit.

3. Standard Deviation of Unit Weight ($S_0$)

The standard deviation of unit weight measures the average residual per degree of freedom:

$$ S_0 = \sqrt{\frac{\text{SSE}}{n - e}} $$

where $n$ is the number of observations and $e$ is the number of unknowns. Significance: $S_0$ is a measure of the model's overall accuracy.

4. Cofactor Matrix ($Q_{xx}$)

The cofactor matrix is computed as:

$$ Q_{xx} = N^{-1} $$

where $N = A^TA$.

5. Covariance Matri ($C_{xx}$)

The covariance matrix is computed as:

$$ C_{xx} = S_0^2 \cdot Q_{xx} $$

Significance: The covariance matrix is crucial for evaluating parameter uncertainties.

6. Dilution of Precision (DOPs)

DOP metrics quantify the geometric quality of the satellite configuration:

• Positional DOP (PDOP):

$$ \text{PDOP} = \sqrt{q_X + q_Y + q_Z} $$

• Time DOP (TDOP):

$$ \text{TDOP} = \sqrt{q_{dT}} $$

• Geometric DOP (GDOP):

$$ \text{GDOP} = \sqrt{\text{PDOP}^2 + \text{TDOP}^2} $$

where $q_X, q_Y, q_Z, q_{dT}$ are the diagonal elements of the cofactor matrix. Significance: Smaller DOP values indicate better satellite geometry and more reliable positioning.

7. Standard Deviations

Standard deviations represent the precision of the estimated parameters:

$$ S_x = \sqrt{C_{xx}[0, 0]}, \quad S_y = \sqrt{C_{xx}[1, 1]}, \quad S_z = \sqrt{C_{xx}[2, 2]}, \quad S_t = \sqrt{C_{xx}[3, 3]} $$

Significance: These values quantify the uncertainty in the estimated receiver coordinates and clock bias.

Computation Workflow

The following steps summarize the computation of these statistical parameters:

• Compute Residuals

$$ V = A \cdot h - l $$

• Calculate SSE

$$ \text{SSE} = V^T \cdot V $$

• Compute $S_0$

$$ S_0 = \sqrt{\frac{\text{SSE}}{n - e}} $$

• Derive $Q_{xx}$

$$ Q_{xx} = N^{-1}, \quad N = A^T \cdot A $$

• Calculate $C_{xx}$

$$ C_{xx} = S_0^2 \cdot Q_{xx} $$

• Extract Cofactors ($q_X, q_Y, q_Z, q_{dT}$) from $Q_{xx}$

• Compute DOPs

$$ \text{PDOP}, \text{TDOP}, \text{GDOP} $$

• Calculate Standard Deviations

$$ S_x, S_y, S_z, S_t $$

Summary

A comprehensive statistical report includes:

• Residuals ($V$): Quantifies model fit.
• SSE: Total error.
• Standard Deviation of Unit Weight ($S_0$): Average error per degree of freedom.
• Covariance Matrix ($C_{xx}$): Absolute parameter precision.
• Cofactor Matrix ($Q_{xx}$): Diagonal elements used to compute DOP values.
• DOPs: Geometric quality of satellite configuration. Low values indicates good satellite geometry.
• Standard Deviations: Uncertainty in receiver coordinates and clock bias.