Product
Redesigned Repositories Page: A Faster Way to Prioritize Security Risk
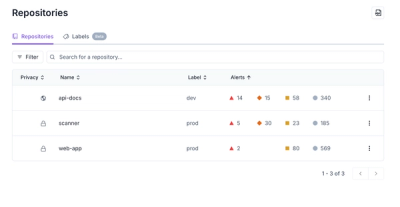
Our redesigned Repositories page adds alert severity, filtering, and tabs for faster triage and clearer insights across all your projects.

HyperJet — Algorithmic Differentiation with Hyper-Dual numbers for Python and C++
A header-only library for algorithmic differentiation with hyper-dual numbers. Written in C++17 with an extensive Python interface.
pip install hyperjet
Import the module:
import hyperjet as hj
Create a set of variables e.g. x=3 and y=6:
x, y = hj.variables([3, 6])
x and y are hyper-dual numbers. This is indicated by the postfix hj:
x
>>> 3hj
Get the value as a simple float:
x.f
>>> 3
The hyper-dual number stores the derivatives as a numpy array.
Get the first order derivatives (Gradient) of a hyper-dual number:
x.g # = [dx/dx, dx/dy]
>>> array([1., 0.])
Get the second order derivatives (Hessian matrix):
x.hm() # = [[d^2 x/ dx**2 , d^2 x/(dx*dy)],
# [d^2 x/(dx*dy), d^2 x/ dy**2 ]]
>>> array([[0., 0.],
[0., 0.]])
For a simple variable these derivatives are trivial.
Now do some computations:
f = (x * y) / (x - y)
f
>>> -6hj
The result is again a hyper-dual number.
Get the first order derivatives of f with respect to x and y:
f.g # = [df/dx, df/dy]
>>> array([-4., 1.])
Get the second order derivatives of f:
f.hm() # = [[d^2 f/ dx**2 , d^2 f/(dx*dy)],
# [d^2 f/(dx*dy), d^2 f/ dy**2 ]]
>>> array([[-2.66666667, 1.33333333],
[ 1.33333333, -0.66666667]])
You can use numpy to perform vector and matrix operations.
Compute the nomalized cross product of two vectors u = [1, 2, 2] and v = [4, 1, -1] with hyper-dual numbers:
import numpy as np
variables = hj.DDScalar.variables([1, 2, 2,
4, 1, -1])
u = np.array(variables[:3]) # = [1hj, 2hj, 2hj]
v = np.array(variables[3:]) # = [4hj, 1hj, -1hj]
normal = np.cross(u, v)
normal /= np.linalg.norm(normal)
normal
>>> array([-0.331042hj, 0.744845hj, -0.579324hj], dtype=object)
The result is a three-dimensional numpy array containing hyper-dual numbers.
Get the value and derivatives of the x-component:
normal[0].f
>>> -0.3310423554409472
normal[0].g
>>> array([ 0.00453483, -0.01020336, 0.00793595, 0.07255723, -0.16325376, 0.12697515])
normal[0].hm()
>>> array([[ 0.00434846, -0.01091775, 0.00647611, -0.0029818 , -0.01143025, -0.02335746],
[-0.01091775, 0.02711578, -0.01655522, 0.00444165, 0.03081974, 0.04858632],
[ 0.00647611, -0.01655522, 0.0093492 , -0.00295074, -0.02510461, -0.03690759],
[-0.0029818 , 0.00444165, -0.00295074, -0.02956956, 0.03025289, -0.01546811],
[-0.01143025, 0.03081974, -0.02510461, 0.03025289, 0.01355789, -0.02868433],
[-0.02335746, 0.04858632, -0.03690759, -0.01546811, -0.02868433, 0.03641839]])
If you use HyperJet, please refer to the official GitHub repository:
@misc{HyperJet,
author = "Thomas Oberbichler",
title = "HyperJet",
howpublished = "\url{http://github.com/oberbichler/HyperJet}",
}
FAQs
Automatic differentiation with dual numbers
We found that hyperjet demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Product
Our redesigned Repositories page adds alert severity, filtering, and tabs for faster triage and clearer insights across all your projects.

Security News
Slopsquatting is a new supply chain threat where AI-assisted code generators recommend hallucinated packages that attackers register and weaponize.

Security News
Multiple deserialization flaws in PyTorch Lightning could allow remote code execution when loading untrusted model files, affecting versions up to 2.4.0.