
Security News
Astral Launches pyx: A Python-Native Package Registry
Astral unveils pyx, a Python-native package registry in beta, designed to speed installs, enhance security, and integrate deeply with uv.
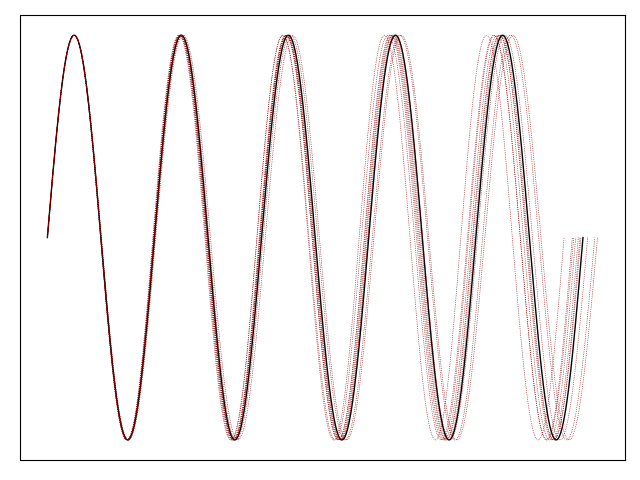
A module calculating the stochastic deviations in timepoints for atomic clocks.
This module is an application of the theory presented in Galleani et al. (2003), doi:10.1088/0026-1394/40/3/305.
The module's current functionality calculates stochastic deviations using the exact iterative solution to the stochastic differential equation in Galleani_exact()
$$\begin{equation*} \mathbf{X}(t_{n+1}) = \begin{pmatrix} 1 & \delta t \\ 0 & 1 \end{pmatrix} \mathbf{X}(t_n) + \begin{pmatrix} \delta t \mu_1 + \frac{1}{2} \delta t^2 \mu_2 \\ \delta t \mu_2 \end{pmatrix} + \mathbf{\Sigma}(t_n) \end{equation*}$$
$$\begin{equation*} \mathbf{\Sigma}(t_n) \sim \mathcal{N} \bigg( \mathbf{0}, \begin{bmatrix} \sigma_1^2 \delta t + \frac{1}{3} \sigma_2^2 \delta t^3 & \frac{1}{2}\sigma_2^2 \delta t^2 \\ \frac{1}{2}\sigma_2^2 \delta t^2 & \sigma_2^2 \delta t \end{bmatrix} \bigg) \end{equation*}$$
Stochastic deviations can be visualised using clock_error(), and their distributions simulated with deviation_distribution().
Please consult the Jupyter notebook for a walkthrough of the package.
FAQs
Atomic clock simulation
We found that stochasticclock demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Security News
Astral unveils pyx, a Python-native package registry in beta, designed to speed installs, enhance security, and integrate deeply with uv.
Security News
The Latio podcast explores how static and runtime reachability help teams prioritize exploitable vulnerabilities and streamline AppSec workflows.

Security News
The latest Opengrep releases add Apex scanning, precision rule tuning, and performance gains for open source static code analysis.