Product
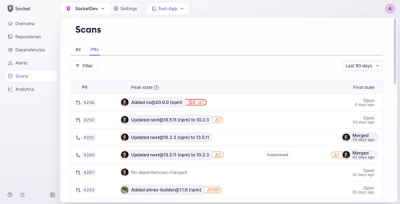
Introducing Pull Request Stories to Help Security Teams Track Supply Chain Risks
Socket’s new Pull Request Stories give security teams clear visibility into dependency risks and outcomes across scanned pull requests.
Transformations is a Python library for calculating 4x4 matrices for translating, rotating, reflecting, scaling, shearing, projecting, orthogonalizing, and superimposing arrays of 3D homogeneous coordinates as well as for converting between rotation matrices, Euler angles, and quaternions. Also includes an Arcball control object and functions to decompose transformation matrices.
The transformations library is no longer actively developed.
:Author: Christoph Gohlke <https://www.cgohlke.com>_
:License: BSD-3-Clause
:Version: 2025.8.1
Install the transformations package and all dependencies from the
Python Package Index <https://pypi.org/project/transformations/>_::
python -m pip install -U transformations
See Examples_ for using the programming interface.
Source code and support are available on
GitHub <https://github.com/cgohlke/transformations>_.
This revision was tested with the following requirements and dependencies (other versions may work):
CPython <https://www.python.org>_ 3.11.9, 3.12.10, 3.13.5, 3.14.0rc 64-bitNumPy <https://pypi.org/project/numpy/>_ 2.3.22025.8.1
2025.1.1
2024.5.24
2024.4.24
2024.1.6
2022.9.26
2022.8.26
2021.6.6
2020.1.1
2019.4.22
Transformations.py is no longer actively developed and has a few known issues and numerical instabilities. The module is mostly superseded by other modules for 3D transformations and quaternions:
Pytransform3d <https://github.com/dfki-ric/pytransform3d>_Scipy.spatial.transform <https://github.com/scipy/scipy/tree/main/scipy/spatial/transform>_Transforms3d <https://github.com/matthew-brett/transforms3d>_
(includes most code of this module)Numpy-quaternion <https://github.com/moble/quaternion>_Blender.mathutils <https://docs.blender.org/api/master/mathutils.html>_The API is not stable yet and is expected to change between revisions.
This Python code is not optimized for speed. Refer to the transformations.c module for a faster implementation of some functions.
Documentation in HTML format can be generated with epydoc.
Matrices (M) can be inverted using numpy.linalg.inv(M), be concatenated using numpy.dot(M0, M1), or transform homogeneous coordinate arrays (v) using numpy.dot(M, v) for shape (4, -1) column vectors, respectively numpy.dot(v, M.T) for shape (-1, 4) row vectors ("array of points").
This module follows the "column vectors on the right" and "row major storage" (C contiguous) conventions. The translation components are in the right column of the transformation matrix, i.e. M[:3, 3]. The transpose of the transformation matrices may have to be used to interface with other graphics systems, e.g. OpenGL's glMultMatrixd(). See also [16].
Calculations are carried out with numpy.float64 precision.
Vector, point, quaternion, and matrix function arguments are expected to be "array like", i.e. tuple, list, or numpy arrays.
Return types are numpy arrays unless specified otherwise.
Angles are in radians unless specified otherwise.
Quaternions w+ix+jy+kz are represented as [w, x, y, z].
A triple of Euler angles can be applied/interpreted in 24 ways, which can be specified using a 4 character string or encoded 4-tuple:
Axes 4-string: e.g. 'sxyz' or 'ryxy'
Axes 4-tuple: e.g. (0, 0, 0, 0) or (1, 1, 1, 1)
alpha, beta, gamma = 0.123, -1.234, 2.345 origin, xaxis, yaxis, zaxis = [0, 0, 0], [1, 0, 0], [0, 1, 0], [0, 0, 1] I = identity_matrix() Rx = rotation_matrix(alpha, xaxis) Ry = rotation_matrix(beta, yaxis) Rz = rotation_matrix(gamma, zaxis) R = concatenate_matrices(Rx, Ry, Rz) euler = euler_from_matrix(R, 'rxyz') numpy.allclose([alpha, beta, gamma], euler) True Re = euler_matrix(alpha, beta, gamma, 'rxyz') is_same_transform(R, Re) True al, be, ga = euler_from_matrix(Re, 'rxyz') is_same_transform(Re, euler_matrix(al, be, ga, 'rxyz')) True qx = quaternion_about_axis(alpha, xaxis) qy = quaternion_about_axis(beta, yaxis) qz = quaternion_about_axis(gamma, zaxis) q = quaternion_multiply(qx, qy) q = quaternion_multiply(q, qz) Rq = quaternion_matrix(q) is_same_transform(R, Rq) True S = scale_matrix(1.23, origin) T = translation_matrix([1, 2, 3]) Z = shear_matrix(beta, xaxis, origin, zaxis) R = random_rotation_matrix(numpy.random.rand(3)) M = concatenate_matrices(T, R, Z, S) scale, shear, angles, trans, persp = decompose_matrix(M) numpy.allclose(scale, 1.23) True numpy.allclose(trans, [1, 2, 3]) True numpy.allclose(shear, [0, math.tan(beta), 0]) True is_same_transform(R, euler_matrix(axes='sxyz', *angles)) True M1 = compose_matrix(scale, shear, angles, trans, persp) is_same_transform(M, M1) True v0, v1 = random_vector(3), random_vector(3) M = rotation_matrix(angle_between_vectors(v0, v1), vector_product(v0, v1)) v2 = numpy.dot(v0, M[:3, :3].T) numpy.allclose(unit_vector(v1), unit_vector(v2)) True
FAQs
Homogeneous Transformation Matrices and Quaternions
We found that transformations demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Product
Socket’s new Pull Request Stories give security teams clear visibility into dependency risks and outcomes across scanned pull requests.
Research
/Security News
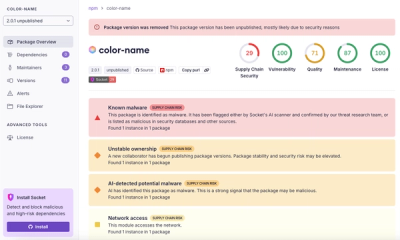
npm author Qix’s account was compromised, with malicious versions of popular packages like chalk-template, color-convert, and strip-ansi published.

Research
Four npm packages disguised as cryptographic tools steal developer credentials and send them to attacker-controlled Telegram infrastructure.