
Security News
CISA’s 2025 SBOM Guidance Adds Hashes, Licenses, Tool Metadata, and Context
CISA’s 2025 draft SBOM guidance adds new fields like hashes, licenses, and tool metadata to make software inventories more actionable.
PerfectShape is a collection of pure Ruby geometric algorithms that are mostly useful for GUI (Graphical User Interface) manipulation like checking viewport rectangle intersection or containment of a mouse click point in popular geometry shapes such as rectangle, square, arc (open, chord, and pie), ellipse, circle, polygon, and paths containing lines, quadratic bézier curves, and cubic bezier curves, potentially with affine transforms applied like translation, scale, rotation, shear/skew, and inversion (including both the Ray Casting Algorithm, aka Even-odd Rule, and the Winding Number Algorithm, aka Nonzero Rule).
Additionally, PerfectShape::Math contains some purely mathematical algorithms, like IEEE 754-1985 Remainder.
To ensure accuracy and precision, this library does all its mathematical operations with BigDecimal numbers.
Run:
gem install perfect-shape -v 1.0.8
Or include in Bundler Gemfile:
gem 'perfect-shape', '~> 1.0.8'
And, run:
bundle
PerfectShape::MathModule
::degrees_to_radians(angle): converts degrees to radians::radians_to_degrees(angle): converts radians to degrees::normalize_degrees(angle): normalizes the specified angle into the range -180 to 180.::ieee_remainder(x, y) (alias: ieee754_remainder): IEEE 754-1985 Remainder (different from standard % modulo operator as it operates on floats and could return a negative result)PerfectShape::ShapeClass
This is a base class for all shapes. It is not meant to be used directly. Subclasses implement/override its methods as needed.
#min_x: min x#min_y: min y#max_x: max x#max_y: max y#width: width#height: height#center_point: center point as Array of [center_x, center_y] coordinates#center_x: center x#center_y: center y#bounding_box: bounding box is a rectangle with x = min x, y = min y, and width/height just as those of shape#==(other): Returns true if equal to other or false otherwise#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0): checks if point is inside if outline is false or if point is on the outline if outline is true. distance_tolerance can be used as a fuzz factor when outline is true, for example, to help GUI users mouse-click-select a shape from its outline more successfullyPerfectShape::PointLocationModule
#initialize(x: 0, y: 0): initializes a point location, usually representing the top-left point in a shape#x: top-left x#y: top-left y#min_x: min x (x by default)#min_y: min y (y by default)#first_point: first point for shape including this module (always assumes top-left corner)PerfectShape::RectangularShapeModule
Includes PerfectShape::PointLocation
#initialize(x: 0, y: 0, width: 1, height: 1): initializes a rectangular shape#x: top-left x#y: top-left y#width: width#height: height#min_x: min x#min_y: min y#max_x: max x#max_y: max yPerfectShape::MultiPointModule
::normalize_point_array: normalizes Array of multiple points into (x,y) point coordinate Array format per point#initialize(points: []): initializes points with Array of multiple points (e.g. useful for shapes like Line and Polygon).#points: Array of multiple points#min_x: min x of all points#min_y: min y of all points#max_x: max x of all points#max_y: max y of all points#first_point: first point for shape including this modulePerfectShape::AffineTransformClass
Affine transforms have the following matrix:
[ xxp xyp xt ]
[ yxp yyp yt ]
The matrix is used to transform (x,y) point coordinates as follows:
[ xxp xyp xt ] * [x] = [ xxp * x + xyp * y + xt ]
[ yxp yyp yt ] * [y] = [ yxp * x + yyp * y + yt ]
xxp is the x coordinate x product (m11)
xyp is the x coordinate y product (m12)
yxp is the y coordinate x product (m21)
yyp is the y coordinate y product (m22)
xt is the x coordinate translation (m13)
yt is the y coordinate translation (m23)
Affine transform mutation operations ending with ! can be chained as they all return self.
::new(xxp_element = nil, xyp_element = nil, yxp_element = nil, yyp_element = nil, xt_element = nil, yt_element = nil, xxp: nil, xyp: nil, yxp: nil, yyp: nil, xt: nil, yt: nil, m11: nil, m12: nil, m21: nil, m22: nil, m13: nil, m23: nil):
The constructor accepts either the (x,y)-operation related argument/kwarg names or traditional matrix element kwarg names. If no arguments are supplied, it constructs an identity matrix (i.e. like calling ::new(xxp: 1, xyp: 0, yxp: 0, yyp: 1, xt: 0, yt: 0)).#matrix_3d: Returns Ruby Matrix object representing affine transform in 3D (used internally for performing multiplication)#==(other): Returns true if equal to other or false otherwise#identity! (alias: reset!): Resets to identity matrix (i.e. like calling ::new(xxp: 1, xyp: 0, yxp: 0, yyp: 1, xt: 0, yt: 0))#invertible? Returns true if matrix is invertible and false otherwise#invert!: Inverts affine transform matrix if invertible or raises an error otherwise#multiply!(other): Multiplies affine transform with another affine transform, storing resulting changes in matrix elements#translate!(x_or_point, y=nil): Translates affine transform with (x, y) translation values#scale!(x_or_point, y=nil): Scales affine transform with (x, y) scale values#rotate!(degrees): Rotates by angle degrees counter-clockwise if angle value is positive or clockwise if angle value is negative. Note that it returns very close approximate results for rotations that are 90/180/270 degrees (good enough for inverse-transform GUI point containment checks needed when checking if mouse-click-point is inside a transformed shape).#shear!(x_or_point, y=nil): Shears by x and y factors#clone: Returns a new AffineTransform with the same matrix elements#transform_point(x_or_point, y=nil): returns [xxp * x + xyp * y + xt, yxp * x + yyp * y + yt]. Note that result is a close approximation, but should be good enough for GUI mouse-click-point containment checks.#transform_points(*xy_coordinates_or_points): returns Array of (x,y) pair Arrays transformed with #transform_point method#inverse_transform_point(x_or_point, y=nil): returns inverse transform of a point (x,y) coordinates (clones self and inverts clone, and then transforms point). Note that result is a close approximation, but should be good enough for GUI mouse-click-point containment checks.#inverse_transform_points(*xy_coordinates_or_points): returns inverse transforms of a point Array of (x,y) coordinatesExample:
xxp = 2
xyp = 3
yxp = 4
yyp = 5
xt = 6
yt = 7
affine_transform1 = PerfectShape::AffineTransform.new(xxp: xxp, xyp: xyp, yxp: yxp, yyp: yyp, xt: xt, yt: yt) # (x,y)-operation kwarg names
affine_transform2 = PerfectShape::AffineTransform.new(m11: xxp, m12: xyp, m21: yxp, m22: yyp, m13: xt, m23: yt) # traditional matrix element kwarg names
affine_transform3 = PerfectShape::AffineTransform.new(xxp, xyp, yxp, yyp, xt, yt) # standard arguments
affine_transform2.matrix_3d == affine_transform1.matrix_3d # => true
affine_transform3.matrix_3d == affine_transform1.matrix_3d # => true
affine_transform = PerfectShape::AffineTransform.new.translate!(30, 20).scale!(2, 3)
affine_transform.transform_point(10, 10) # => approximately [50, 50]
affine_transform.inverse_transform_point(50, 50) # => approximately [10, 10]
PerfectShape::PointClass
Extends PerfectShape::Shape
Includes PerfectShape::PointLocation

Points are simply represented by an Array of [x,y] coordinates when used within other shapes, but when needing point-specific operations like point_distance, the PerfectShape::Point class can come in handy.
::point_distance(x, y, px, py): Returns the distance from a point to another point::normalize_point(x_or_point, y = nil): Normalizes point args whether two-number point Array or x, y args, returning normalized point Array of two BigDecimal's::new(x_or_point=nil, y_arg=nil, x: nil, y: nil): constructs a point with (x,y) pair (default: 0,0) whether specified as Array of (x,y) pair, flat x,y args, or x:, y: kwargs.#min_x: min x (always x)#min_y: min y (always y)#max_x: max x (always x)#max_y: max y (always y)#width: width (always 0)#height: height (always 0)#center_point: center point as Array of [center_x, center_y] coordinates#center_x: center x (always x)#center_y: center y (always y)#bounding_box: bounding box is a rectangle with x = min x, y = min y, and width/height of shape#==(other): Returns true if equal to other or false otherwise#contain?(x_or_point, y=nil, outline: true, distance_tolerance: 0): checks if point matches self, with a distance tolerance (0 by default). Distance tolerance provides a fuzz factor that for example enables GUI users to mouse-click-select a point shape more successfully. outline option makes no difference on point#intersect?(rectangle): Returns true if intersecting with interior of rectangle or false otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing#point_distance(x_or_point, y=nil): Returns the distance from a point to another pointExample:
require 'perfect-shape'
shape = PerfectShape::Point.new(x: 200, y: 150)
shape.contain?(200, 150) # => true
shape.contain?([200, 150]) # => true
shape.contain?(200, 151) # => false
shape.contain?([200, 151]) # => false
shape.contain?(200, 151, distance_tolerance: 5) # => true
shape.contain?([200, 151], distance_tolerance: 5) # => true
PerfectShape::LineClass
Extends PerfectShape::Shape
Includes PerfectShape::MultiPoint

::relative_counterclockwise(x1, y1, x2, y2, px, py): Returns an indicator of where the specified point (px,py) lies with respect to the line segment from (x1,y1) to (x2,y2). The return value can be either 1, -1, or 0 and indicates in which direction the specified line must pivot around its first end point, (x1,y1), in order to point at the specified point (px,py). A return value of 1 indicates that the line segment must turn in the direction that takes the positive X axis towards the negative Y axis. In the default coordinate system, this direction is counterclockwise. A return value of -1 indicates that the line segment must turn in the direction that takes the positive X axis towards the positive Y axis. In the default coordinate system, this direction is clockwise. A return value of 0 indicates that the point lies exactly on the line segment. Note that an indicator value of 0 is rare and not useful for determining collinearity because of floating point rounding issues. If the point is colinear with the line segment, but not between the end points, then the value will be -1 if the point lies “beyond (x1,y1)” or 1 if the point lies “beyond (x2,y2)”.::point_distance_square(x1, y1, x2, y2, px, py): Returns the square of distance from a point to a line segment.::point_distance(x1, y1, x2, y2, px, py): Returns the distance from a point to a line segment.::new(points: []): constructs a line with two points as Array of Arrays of [x,y] pairs or flattened Array of alternating x and y coordinates#min_x: min x#min_y: min y#max_x: max x#max_y: max y#width: width (from min x to max x)#height: height (from min y to max y)#center_point: center point as Array of [center_x, center_y] coordinates#center_x: center x#center_y: center y#bounding_box: bounding box is a rectangle with x = min x, y = min y, and width/height of shape#==(other): Returns true if equal to other or false otherwise#contain?(x_or_point, y=nil, outline: true, distance_tolerance: 0): checks if point lies on line, with a distance tolerance (0 by default). Distance tolerance provides a fuzz factor that for example enables GUI users to mouse-click-select a line shape more successfully. outline option makes no difference on line#intersect?(rectangle): Returns true if intersecting with interior of rectangle or false otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing#relative_counterclockwise(x_or_point, y=nil): Returns an indicator of where the specified point (px,py) lies with respect to the line segment from (x1,y1) to (x2,y2). The return value can be either 1, -1, or 0 and indicates in which direction the specified line must pivot around its first end point, (x1,y1), in order to point at the specified point (px,py). A return value of 1 indicates that the line segment must turn in the direction that takes the positive X axis towards the negative Y axis. In the default coordinate system, this direction is counterclockwise. A return value of -1 indicates that the line segment must turn in the direction that takes the positive X axis towards the positive Y axis. In the default coordinate system, this direction is clockwise. A return value of 0 indicates that the point lies exactly on the line segment. Note that an indicator value of 0 is rare and not useful for determining collinearity because of floating point rounding issues. If the point is colinear with the line segment, but not between the end points, then the value will be -1 if the point lies “beyond (x1,y1)” or 1 if the point lies “beyond (x2,y2)”.#point_distance(x_or_point, y=nil): Returns the distance from a point to a line segment.#rect_crossings(rxmin, rymin, rxmax, rymax, crossings = 0): rectangle crossings (adds to crossings arg)Example:
require 'perfect-shape'
shape = PerfectShape::Line.new(points: [[0, 0], [100, 100]]) # start point and end point
shape.contain?(50, 50) # => true
shape.contain?([50, 50]) # => true
shape.contain?(50, 51) # => false
shape.contain?([50, 51]) # => false
shape.contain?(50, 51, distance_tolerance: 5) # => true
shape.contain?([50, 51], distance_tolerance: 5) # => true
PerfectShape::QuadraticBezierCurveClass
Extends PerfectShape::Shape
Includes PerfectShape::MultiPoint

::tag(coord, low, high): Determine where coord lies with respect to the range from low to high. It is assumed that low < high. The return value is one of the 5 values BELOW, LOWEDGE, INSIDE, HIGHEDGE, or ABOVE.::eqn(val, c1, cp, c2): Fill an array with the coefficients of the parametric equation in t, ready for solving against val with solve_quadratic. We currently have: val = Py(t) = C1*(1-t)^2 + 2CPt*(1-t) + C2t^2 = C1 - 2C1t + C1t^2 + 2CPt - 2CPt^2 + C2t^2 = C1 + (2CP - 2C1)t + (C1 - 2CP + C2)t^2; 0 = (C1 - val) + (2CP - 2C1)t + (C1 - 2CP + C2)t^2; 0 = C + Bt + At^2; C = C1 - val; B = 2CP - 2C1; A = C1 - 2CP + C2::solve_quadratic(eqn): Solves the quadratic whose coefficients are in the eqn array and places the non-complex roots into the res array, returning the number of roots. The quadratic solved is represented by the equation: eqn = {C, B, A}; ax^2 + bx + c = 0 A return value of -1 is used to distinguish a constant equation, which might be always 0 or never 0, from an equation that has no zeroes.::eval_quadratic(vals, num, include0, include1, inflect, c1, ctrl, c2): Evaluate the t values in the first num slots of the vals[] array and place the evaluated values back into the same array. Only evaluate t values that are within the range <, >, including the 0 and 1 ends of the range iff the include0 or include1 booleans are true. If an "inflection" equation is handed in, then any points which represent a point of inflection for that quadratic equation are also ignored.::new(points: []): constructs a quadratic bézier curve with three points (start point, control point, and end point) as Array of Arrays of [x,y] pairs or flattened Array of alternating x and y coordinates#points: points (start point, control point, and end point)#min_x: min x#min_y: min y#max_x: max x#max_y: max y#width: width (from min x to max x)#height: height (from min y to max y)#center_point: center point as Array of [center_x, center_y] coordinates#center_x: center x#center_y: center y#bounding_box: bounding box is a rectangle with x = min x, y = min y, and width/height of shape (bounding box only guarantees that the shape is within it, but it might be bigger than the shape)#==(other): Returns true if equal to other or false otherwise#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0): checks if point is inside when outline is false or if point is on the outline when outline is true. distance_tolerance can be used as a fuzz factor when outline is true, for example, to help GUI users mouse-click-select a quadratic bezier curve shape from its outline more successfully#intersect?(rectangle): Returns true if intersecting with interior of rectangle or false otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing#curve_center_point: point at the center of the curve outline (not the center of the bounding box area like center_x and center_y)#curve_center_x: point x coordinate at the center of the curve outline (not the center of the bounding box area like center_x and center_y)#curve_center_y: point y coordinate at the center of the curve outline (not the center of the bounding box area like center_x and center_y)#subdivisions(level=1): subdivides quadratic bezier curve at its center into into 2 quadratic bezier curves by default, or more if level of recursion is specified. The resulting number of subdivisions is 2 to the power of level.#point_distance(x_or_point, y=nil, minimum_distance_threshold: OUTLINE_MINIMUM_DISTANCE_THRESHOLD): calculates distance from point to curve segment. It does so by subdividing curve into smaller curves and checking against the curve center points until the distance is less than minimum_distance_threshold, to avoid being an overly costly operation.#rect_crossings(rxmin, rymin, rxmax, rymax, level, crossings = 0): rectangle crossings (adds to crossings arg)Example:
require 'perfect-shape'
shape = PerfectShape::QuadraticBezierCurve.new(points: [[200, 150], [270, 320], [380, 150]]) # start point, control point, and end point
shape.contain?(270, 220) # => true
shape.contain?([270, 220]) # => true
shape.contain?(270, 220, outline: true) # => false
shape.contain?([270, 220], outline: true) # => false
shape.contain?(280, 235, outline: true) # => true
shape.contain?([280, 235], outline: true) # => true
shape.contain?(281, 235, outline: true) # => false
shape.contain?([281, 235], outline: true) # => false
shape.contain?(281, 235, outline: true, distance_tolerance: 1) # => true
shape.contain?([281, 235], outline: true, distance_tolerance: 1) # => true
PerfectShape::CubicBezierCurveClass
Extends PerfectShape::Shape
Includes PerfectShape::MultiPoint

::new(points: []): constructs a cubic bézier curve with four points (start point, two control points, and end point) as Array of Arrays of [x,y] pairs or flattened Array of alternating x and y coordinates#points: points (start point, two control points, and end point)#min_x: min x#min_y: min y#max_x: max x#max_y: max y#width: width (from min x to max x)#height: height (from min y to max y)#center_point: center point as Array of [center_x, center_y] coordinates#center_x: center x#center_y: center y#bounding_box: bounding box is a rectangle with x = min x, y = min y, and width/height of shape (bounding box only guarantees that the shape is within it, but it might be bigger than the shape)#==(other): Returns true if equal to other or false otherwise#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0): checks if point is inside when outline is false or if point is on the outline when outline is true. distance_tolerance can be used as a fuzz factor when outline is true, for example, to help GUI users mouse-click-select a cubic bezier curve shape from its outline more successfully#intersect?(rectangle): Returns true if intersecting with interior of rectangle or false otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing#curve_center_point: point at the center of the curve outline (not the center of the bounding box area like center_x and center_y)#curve_center_x: point x coordinate at the center of the curve outline (not the center of the bounding box area like center_x and center_y)#curve_center_y: point y coordinate at the center of the curve outline (not the center of the bounding box area like center_x and center_y)#subdivisions(level=1): subdivides cubic bezier curve at its center into into 2 cubic bezier curves by default, or more if level of recursion is specified. The resulting number of subdivisions is 2 to the power of level.#point_distance(x_or_point, y=nil, minimum_distance_threshold: OUTLINE_MINIMUM_DISTANCE_THRESHOLD): calculates distance from point to curve segment. It does so by subdividing curve into smaller curves and checking against the curve center points until the distance is less than minimum_distance_threshold, to avoid being an overly costly operation.#rectangle_crossings(rectangle): rectangle crossings (used to determine rectangle interior intersection), optimized to check if line represented by cubic bezier curve crosses the rectangle first, and if not then perform expensive check with #rect_crossings#rect_crossings(rxmin, rymin, rxmax, rymax, level, crossings = 0): rectangle crossings (adds to crossings arg)Example:
require 'perfect-shape'
shape = PerfectShape::CubicBezierCurve.new(points: [[200, 150], [235, 235], [270, 320], [380, 150]]) # start point, two control points, and end point
shape.contain?(270, 220) # => true
shape.contain?([270, 220]) # => true
shape.contain?(270, 220, outline: true) # => false
shape.contain?([270, 220], outline: true) # => false
shape.contain?(261.875, 245.625, outline: true) # => true
shape.contain?([261.875, 245.625], outline: true) # => true
shape.contain?(261.875, 246.625, outline: true) # => false
shape.contain?([261.875, 246.625], outline: true) # => false
shape.contain?(261.875, 246.625, outline: true, distance_tolerance: 1) # => true
shape.contain?([261.875, 246.625], outline: true, distance_tolerance: 1) # => true
PerfectShape::RectangleClass
Extends PerfectShape::Shape
Includes PerfectShape::RectangularShape

::new(x: 0, y: 0, width: 1, height: 1): constructs a rectangle#x: top-left x#y: top-left y#width: width#height: height#center_point: center point as Array of [center_x, center_y] coordinates#center_x: center x#center_y: center y#min_x: min x#min_y: min y#max_x: max x#max_y: max y#bounding_box: bounding box is a rectangle with x = min x, y = min y, and width/height of shape#==(other): Returns true if equal to other or false otherwise#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0): checks if point is inside when outline is false or if point is on the outline when outline is true. distance_tolerance can be used as a fuzz factor when outline is true, for example, to help GUI users mouse-click-select a rectangle shape from its outline more successfully#intersect?(rectangle): Returns true if intersecting with interior of rectangle or false otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing#edges: edges of rectangle as PerfectShape::Line objects#out_state(x_or_point, y = nil): Returns "out state" of specified point (x,y) (whether it lies to the left, right, top, bottom of rectangle). If point is outside rectangle, it returns a bit mask combination of Rectangle::OUT_LEFT, Rectangle::OUT_RIGHT, Rectangle::OUT_TOP, or Rectangle::OUT_BOTTOM. Otherwise, it returns 0 if point is inside the rectangle.#empty?: Returns true if width or height are 0 (or negative) and false otherwise#to_path_shapes: Converts Rectangle into basic Path shapes made up of Points and Lines. Used by Path when adding a Rectangle to Path shapesExample:
require 'perfect-shape'
shape = PerfectShape::Rectangle.new(x: 15, y: 30, width: 200, height: 100)
shape.contain?(115, 80) # => true
shape.contain?([115, 80]) # => true
shape.contain?(115, 80, outline: true) # => false
shape.contain?([115, 80], outline: true) # => false
shape.contain?(115, 30, outline: true) # => true
shape.contain?([115, 30], outline: true) # => true
shape.contain?(115, 31, outline: true) # => false
shape.contain?([115, 31], outline: true) # => false
shape.contain?(115, 31, outline: true, distance_tolerance: 1) # => true
shape.contain?([115, 31], outline: true, distance_tolerance: 1) # => true
PerfectShape::SquareClass
Extends PerfectShape::Rectangle

::new(x: 0, y: 0, length: 1) (length alias: size): constructs a square#x: top-left x#y: top-left y#length: length#width: width (equal to length)#height: height (equal to length)#center_point: center point as Array of [center_x, center_y] coordinates#center_x: center x#center_y: center y#min_x: min x#min_y: min y#max_x: max x#max_y: max y#bounding_box: bounding box is a rectangle with x = min x, y = min y, and width/height of shape#==(other): Returns true if equal to other or false otherwise#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0): checks if point is inside when outline is false or if point is on the outline when outline is true. distance_tolerance can be used as a fuzz factor when outline is true, for example, to help GUI users mouse-click-select a square shape from its outline more successfully#intersect?(rectangle): Returns true if intersecting with interior of rectangle or false otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing#edges: edges of square as PerfectShape::Line objects#empty?: Returns true if length is 0 (or negative) and false otherwise#to_path_shapes: Converts Square into basic Path shapes made up of Points and Lines. Used by Path when adding a Square to Path shapesExample:
require 'perfect-shape'
shape = PerfectShape::Square.new(x: 15, y: 30, length: 200)
shape.contain?(115, 130) # => true
shape.contain?([115, 130]) # => true
shape.contain?(115, 130, outline: true) # => false
shape.contain?([115, 130], outline: true) # => false
shape.contain?(115, 30, outline: true) # => true
shape.contain?([115, 30], outline: true) # => true
shape.contain?(115, 31, outline: true) # => false
shape.contain?([115, 31], outline: true) # => false
shape.contain?(115, 31, outline: true, distance_tolerance: 1) # => true
shape.contain?([115, 31], outline: true, distance_tolerance: 1) # => true
PerfectShape::ArcClass
Extends PerfectShape::Shape
Includes PerfectShape::RectangularShape
Arcs can be of type :open, :chord, or :pie
| Open Arc | Chord Arc | Pie Arc |
|---|---|---|
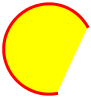 |  |  |
::new(type: :open, x: 0, y: 0, width: 1, height: 1, start: 0, extent: 360, center_x: nil, center_y: nil, radius_x: nil, radius_y: nil): constructs an arc of type :open (default), :chord, or :pie#type: :open, :chord, or :pie#x: top-left x#y: top-left y#width: width#height: height#start: start angle in degrees#extent: extent angle in degrees#center_point: center point as Array of [center_x, center_y] coordinates#start_point: start point as Array of (x,y) coordinates#end_point: end point as Array of (x,y) coordinates#center_x: center x#center_y: center y#radius_x: radius along the x-axis#radius_y: radius along the y-axis#min_x: min x#min_y: min y#max_x: max x#max_y: max y#bounding_box: bounding box is a rectangle with x = min x, y = min y, and width/height of shape#==(other): Returns true if equal to other or false otherwise#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0): checks if point is inside when outline is false or if point is on the outline when outline is true. distance_tolerance can be used as a fuzz factor when outline is true, for example, to help GUI users mouse-click-select an arc shape from its outline more successfully#intersect?(rectangle): Returns true if intersecting with interior of rectangle or false otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing#contain_angle?(angle): returns true if the angle is within the angular extents of the arc and false otherwise#to_path_shapes: Converts Arc into basic Path shapes made up of Points, Lines, and CubicBezierCurves. Used by Path when adding an Arc to Path shapes#btan(increment): btan computes the length (k) of the control segments at the beginning and end of a cubic bezier that approximates a segment of an arc with extent less than or equal to 90 degrees. This length (k) will be used to generate the 2 bezier control points for such a segment.Example:
require 'perfect-shape'
shape = PerfectShape::Arc.new(type: :open, x: 2, y: 3, width: 50, height: 60, start: 45, extent: 270)
shape2 = PerfectShape::Arc.new(type: :open, center_x: 2 + 25, center_y: 3 + 30, radius_x: 25, radius_y: 30, start: 45, extent: 270)
shape.contain?(39.5, 33.0) # => true
shape.contain?([39.5, 33.0]) # => true
shape2.contain?(39.5, 33.0) # => true
shape2.contain?([39.5, 33.0]) # => true
shape.contain?(39.5, 33.0, outline: true) # => false
shape.contain?([39.5, 33.0], outline: true) # => false
shape2.contain?(39.5, 33.0, outline: true) # => false
shape2.contain?([39.5, 33.0], outline: true) # => false
shape.contain?(2.0, 33.0, outline: true) # => true
shape.contain?([2.0, 33.0], outline: true) # => true
shape2.contain?(2.0, 33.0, outline: true) # => true
shape2.contain?([2.0, 33.0], outline: true) # => true
shape.contain?(3.0, 33.0, outline: true) # => false
shape.contain?([3.0, 33.0], outline: true) # => false
shape2.contain?(3.0, 33.0, outline: true) # => false
shape2.contain?([3.0, 33.0], outline: true) # => false
shape.contain?(3.0, 33.0, outline: true, distance_tolerance: 1.0) # => true
shape.contain?([3.0, 33.0], outline: true, distance_tolerance: 1.0) # => true
shape2.contain?(3.0, 33.0, outline: true, distance_tolerance: 1.0) # => true
shape2.contain?([3.0, 33.0], outline: true, distance_tolerance: 1.0) # => true
shape.contain?(shape.center_x, shape.center_y, outline: true) # => false
shape.contain?([shape.center_x, shape.center_y], outline: true) # => false
shape2.contain?(shape2.center_x, shape2.center_y, outline: true) # => false
shape2.contain?([shape2.center_x, shape2.center_y], outline: true) # => false
shape3 = PerfectShape::Arc.new(type: :chord, x: 2, y: 3, width: 50, height: 60, start: 45, extent: 270)
shape4 = PerfectShape::Arc.new(type: :chord, center_x: 2 + 25, center_y: 3 + 30, radius_x: 25, radius_y: 30, start: 45, extent: 270)
shape3.contain?(39.5, 33.0) # => true
shape3.contain?([39.5, 33.0]) # => true
shape4.contain?(39.5, 33.0) # => true
shape4.contain?([39.5, 33.0]) # => true
shape3.contain?(39.5, 33.0, outline: true) # => false
shape3.contain?([39.5, 33.0], outline: true) # => false
shape4.contain?(39.5, 33.0, outline: true) # => false
shape4.contain?([39.5, 33.0], outline: true) # => false
shape3.contain?(2.0, 33.0, outline: true) # => true
shape3.contain?([2.0, 33.0], outline: true) # => true
shape4.contain?(2.0, 33.0, outline: true) # => true
shape4.contain?([2.0, 33.0], outline: true) # => true
shape3.contain?(3.0, 33.0, outline: true) # => false
shape3.contain?([3.0, 33.0], outline: true) # => false
shape4.contain?(3.0, 33.0, outline: true) # => false
shape4.contain?([3.0, 33.0], outline: true) # => false
shape3.contain?(3.0, 33.0, outline: true, distance_tolerance: 1.0) # => true
shape3.contain?([3.0, 33.0], outline: true, distance_tolerance: 1.0) # => true
shape4.contain?(3.0, 33.0, outline: true, distance_tolerance: 1.0) # => true
shape4.contain?([3.0, 33.0], outline: true, distance_tolerance: 1.0) # => true
shape3.contain?(shape3.center_x, shape3.center_y, outline: true) # => false
shape3.contain?([shape3.center_x, shape3.center_y], outline: true) # => false
shape4.contain?(shape4.center_x, shape4.center_y, outline: true) # => false
shape4.contain?([shape4.center_x, shape4.center_y], outline: true) # => false
shape5 = PerfectShape::Arc.new(type: :pie, x: 2, y: 3, width: 50, height: 60, start: 45, extent: 270)
shape6 = PerfectShape::Arc.new(type: :pie, center_x: 2 + 25, center_y: 3 + 30, radius_x: 25, radius_y: 30, start: 45, extent: 270)
shape5.contain?(39.5, 33.0) # => false
shape5.contain?([39.5, 33.0]) # => false
shape6.contain?(39.5, 33.0) # => false
shape6.contain?([39.5, 33.0]) # => false
shape5.contain?(9.5, 33.0) # => true
shape5.contain?([9.5, 33.0]) # => true
shape6.contain?(9.5, 33.0) # => true
shape6.contain?([9.5, 33.0]) # => true
shape5.contain?(39.5, 33.0, outline: true) # => false
shape5.contain?([39.5, 33.0], outline: true) # => false
shape6.contain?(39.5, 33.0, outline: true) # => false
shape6.contain?([39.5, 33.0], outline: true) # => false
shape5.contain?(2.0, 33.0, outline: true) # => true
shape5.contain?([2.0, 33.0], outline: true) # => true
shape6.contain?(2.0, 33.0, outline: true) # => true
shape6.contain?([2.0, 33.0], outline: true) # => true
shape5.contain?(3.0, 33.0, outline: true) # => false
shape5.contain?([3.0, 33.0], outline: true) # => false
shape6.contain?(3.0, 33.0, outline: true) # => false
shape6.contain?([3.0, 33.0], outline: true) # => false
shape5.contain?(3.0, 33.0, outline: true, distance_tolerance: 1.0) # => true
shape5.contain?([3.0, 33.0], outline: true, distance_tolerance: 1.0) # => true
shape6.contain?(3.0, 33.0, outline: true, distance_tolerance: 1.0) # => true
shape6.contain?([3.0, 33.0], outline: true, distance_tolerance: 1.0) # => true
shape5.contain?(shape5.center_x, shape5.center_y, outline: true) # => true
shape5.contain?([shape5.center_x, shape5.center_y], outline: true) # => true
shape6.contain?(shape6.center_x, shape6.center_y, outline: true) # => true
shape6.contain?([shape6.center_x, shape6.center_y], outline: true) # => true
PerfectShape::EllipseClass
Extends PerfectShape::Arc

::new(x: 0, y: 0, width: 1, height: 1, center_x: nil, center_y: nil, radius_x: nil, radius_y: nil): constructs an ellipse#x: top-left x#y: top-left y#width: width#height: height#center_point: center point as Array of [center_x, center_y] coordinates#center_x: center x#center_y: center y#radius_x: radius along the x-axis#radius_y: radius along the y-axis#type: always :open#start: always 0#extent: always 360#min_x: min x#min_y: min y#max_x: max x#max_y: max y#bounding_box: bounding box is a rectangle with x = min x, y = min y, and width/height of shape#==(other): Returns true if equal to other or false otherwise#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0): checks if point is inside when outline is false or if point is on the outline when outline is true. distance_tolerance can be used as a fuzz factor when outline is true, for example, to help GUI users mouse-click-select an ellipse shape from its outline more successfully#intersect?(rectangle): Returns true if intersecting with interior of rectangle or false otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing#to_path_shapes: Converts Ellipse into basic Path shapes made up of Points, Lines, and CubicBezierCurves. Used by Path when adding an Ellipse to Path shapesExample:
require 'perfect-shape'
shape = PerfectShape::Ellipse.new(x: 2, y: 3, width: 50, height: 60)
shape2 = PerfectShape::Ellipse.new(center_x: 27, center_y: 33, radius_x: 25, radius_y: 30)
shape.contain?(27, 33) # => true
shape.contain?([27, 33]) # => true
shape2.contain?(27, 33) # => true
shape2.contain?([27, 33]) # => true
shape.contain?(27, 33, outline: true) # => false
shape.contain?([27, 33], outline: true) # => false
shape2.contain?(27, 33, outline: true) # => false
shape2.contain?([27, 33], outline: true) # => false
shape.contain?(2, 33, outline: true) # => true
shape.contain?([2, 33], outline: true) # => true
shape2.contain?(2, 33, outline: true) # => true
shape2.contain?([2, 33], outline: true) # => true
shape.contain?(1, 33, outline: true) # => false
shape.contain?([1, 33], outline: true) # => false
shape2.contain?(1, 33, outline: true) # => false
shape2.contain?([1, 33], outline: true) # => false
shape.contain?(1, 33, outline: true, distance_tolerance: 1) # => true
shape.contain?([1, 33], outline: true, distance_tolerance: 1) # => true
shape2.contain?(1, 33, outline: true, distance_tolerance: 1) # => true
shape2.contain?([1, 33], outline: true, distance_tolerance: 1) # => true
PerfectShape::CircleClass
Extends PerfectShape::Ellipse

::new(x: 0, y: 0, diameter: 1, width: 1, height: 1, center_x: nil, center_y: nil, radius: nil, radius_x: nil, radius_y: nil): constructs a circle#x: top-left x#y: top-left y#diameter: diameter#width: width (equal to diameter)#height: height (equal to diameter)#center_point: center point as Array of [center_x, center_y] coordinates#center_x: center x#center_y: center y#radius: radius#radius_x: radius along the x-axis (equal to radius)#radius_y: radius along the y-axis (equal to radius)#type: always :open#start: always 0#extent: always 360#min_x: min x#min_y: min y#max_x: max x#max_y: max y#bounding_box: bounding box is a rectangle with x = min x, y = min y, and width/height of shape#==(other): Returns true if equal to other or false otherwise#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0): checks if point is inside when outline is false or if point is on the outline when outline is true. distance_tolerance can be used as a fuzz factor when outline is true, for example, to help GUI users mouse-click-select a circle shape from its outline more successfully#intersect?(rectangle): Returns true if intersecting with interior of rectangle or false otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing#to_path_shapes: Converts Circle into basic Path shapes made up of Points, Lines, and CubicBezierCurves. Used by Path when adding a Circle to Path shapesExample:
require 'perfect-shape'
shape = PerfectShape::Circle.new(x: 2, y: 3, diameter: 60)
shape2 = PerfectShape::Circle.new(center_x: 2 + 30, center_y: 3 + 30, radius: 30)
shape.contain?(32, 33) # => true
shape.contain?([32, 33]) # => true
shape2.contain?(32, 33) # => true
shape2.contain?([32, 33]) # => true
shape.contain?(32, 33, outline: true) # => false
shape.contain?([32, 33], outline: true) # => false
shape2.contain?(32, 33, outline: true) # => false
shape2.contain?([32, 33], outline: true) # => false
shape.contain?(2, 33, outline: true) # => true
shape.contain?([2, 33], outline: true) # => true
shape2.contain?(2, 33, outline: true) # => true
shape2.contain?([2, 33], outline: true) # => true
shape.contain?(1, 33, outline: true) # => false
shape.contain?([1, 33], outline: true) # => false
shape2.contain?(1, 33, outline: true) # => false
shape2.contain?([1, 33], outline: true) # => false
shape.contain?(1, 33, outline: true, distance_tolerance: 1) # => true
shape.contain?([1, 33], outline: true, distance_tolerance: 1) # => true
shape2.contain?(1, 33, outline: true, distance_tolerance: 1) # => true
shape2.contain?([1, 33], outline: true, distance_tolerance: 1) # => true
PerfectShape::PolygonClass
Extends PerfectShape::Shape
Includes PerfectShape::MultiPoint
A polygon can be thought of as a special case of path, consisting of lines only, is closed, and has the Even-Odd winding rule by default.

::new(points: [], winding_rule: :wind_even_odd): constructs a polygon with points as Array of Arrays of [x,y] pairs or flattened Array of alternating x and y coordinates and specified winding rule (:wind_even_odd or :wind_non_zero)#min_x: min x#min_y: min y#max_x: max x#max_y: max y#width: width (from min x to max x)#height: height (from min y to max y)#center_point: center point as Array of [center_x, center_y] coordinates#center_x: center x#center_y: center y#bounding_box: bounding box is a rectangle with x = min x, y = min y, and width/height of shape#==(other): Returns true if equal to other or false otherwise#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0): When outline is false, it checks if point is inside using either the Ray Casting Algorithm (aka Even-Odd Rule) or Winding Number Algorithm (aka Nonzero-Rule). Otherwise, when outline is true, it checks if point is on the outline. distance_tolerance can be used as a fuzz factor when outline is true, for example, to help GUI users mouse-click-select a polygon shape from its outline more successfully#intersect?(rectangle): Returns true if intersecting with interior of rectangle or false otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing#edges: edges of polygon as PerfectShape::Line objectsExample:
require 'perfect-shape'
shape = PerfectShape::Polygon.new(points: [[200, 150], [270, 170], [250, 220], [220, 190], [200, 200], [180, 170]])
shape.contain?(225, 185) # => true
shape.contain?([225, 185]) # => true
shape.contain?(225, 185, outline: true) # => false
shape.contain?([225, 185], outline: true) # => false
shape.contain?(200, 150, outline: true) # => true
shape.contain?([200, 150], outline: true) # => true
shape.contain?(200, 151, outline: true) # => false
shape.contain?([200, 151], outline: true) # => false
shape.contain?(200, 151, outline: true, distance_tolerance: 1) # => true
shape.contain?([200, 151], outline: true, distance_tolerance: 1) # => true
PerfectShape::PathClass
Extends PerfectShape::Shape
Includes PerfectShape::MultiPoint
::new(shapes: [], closed: false, winding_rule: :wind_even_odd, line_to_complex_shapes: false): constructs a path with shapes as Array of shape objects, which can be PerfectShape::Point (or Array of [x, y] coordinates), PerfectShape::Line, PerfectShape::QuadraticBezierCurve, PerfectShape::CubicBezierCurve, or complex shapes that decompose into the aforementioned basic path shapes, like PerfectShape::Arc, PerfectShape::Ellipse, PerfectShape::Circle, PerfectShape::Rectangle, and PerfectShape::Square. If a path is closed, its last point is automatically connected to its first point with a line segment. The winding rule can be :wind_non_zero (default) or :wind_even_odd. line_to_complex_shapes can be true or false (default), indicating whether to connect to complex shapes, meaning Arc, Ellipse, Circle, Rectangle, and Square, with a line, or otherwise move to their start point instead.#shapes: the shapes that the path is composed of (must always start with PerfectShape::Point or Array of [x,y] coordinates representing start point)#basic_shapes: the basic shapes that the path is composed of, meaning only Point, Line, QuadraticBezierCurve, and CubicBezierCurve shapes (decomposing complex shapes like Arc, Ellipse, Circle, Rectangle, and Square, using their #to_path_shapes method)#closed?: returns true if closed and false otherwise#winding_rule: returns winding rule (:wind_non_zero or :wind_even_odd)#points: path points calculated (derived) from shapes#min_x: min x#min_y: min y#max_x: max x#max_y: max y#width: width (from min x to max x)#height: height (from min y to max y)#center_point: center point as Array of [center_x, center_y] coordinates#center_x: center x#center_y: center y#bounding_box: bounding box is a rectangle with x = min x, y = min y, and width/height of shape (bounding box only guarantees that the shape is within it, but it might be bigger than the shape)#==(other): Returns true if equal to other or false otherwise#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0): When outline is false, it checks if point is inside path utilizing the configured winding rule, which can be the Nonzero-Rule (aka Winding Number Algorithm) or the Even-Odd Rule (aka Ray Casting Algorithm). Otherwise, when outline is true, it checks if point is on the outline. distance_tolerance can be used as a fuzz factor when outline is true, for example, to help GUI users mouse-click-select a path shape from its outline more successfully#intersect?(rectangle): Returns true if intersecting with interior of rectangle or false otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawing#point_crossings(x_or_point, y=nil): calculates the number of times the given path crosses the ray extending to the right from (x,y)#disconnected_shapes: Disconnected shapes have their start point filled in so that each shape does not depend on the previous shape to determine its start point. Also, if a point is followed by a non-point shape, it is removed since it is augmented to the following shape as its start point. Lastly, if the path is closed, an extra shape is added to represent the line connecting the last point to the firstExample:
require 'perfect-shape'
path_shapes = []
path_shapes << PerfectShape::Point.new(x: 200, y: 150)
path_shapes << PerfectShape::Line.new(points: [250, 170]) # no need for start point, just end point
path_shapes << PerfectShape::QuadraticBezierCurve.new(points: [[300, 185], [350, 150]]) # no need for start point, just control point and end point
path_shapes << PerfectShape::CubicBezierCurve.new(points: [[370, 50], [430, 220], [480, 170]]) # no need for start point, just two control points and end point
shape = PerfectShape::Path.new(shapes: path_shapes, closed: false, winding_rule: :wind_non_zero)
shape.contain?(275, 165) # => true
shape.contain?([275, 165]) # => true
shape.contain?(275, 165, outline: true) # => false
shape.contain?([275, 165], outline: true) # => false
shape.contain?(shape.disconnected_shapes[1].curve_center_x, shape.disconnected_shapes[1].curve_center_y, outline: true) # => true
shape.contain?([shape.disconnected_shapes[1].curve_center_x, shape.disconnected_shapes[1].curve_center_y], outline: true) # => true
shape.contain?(shape.disconnected_shapes[1].curve_center_x + 1, shape.disconnected_shapes[1].curve_center_y, outline: true) # => false
shape.contain?([shape.disconnected_shapes[1].curve_center_x + 1, shape.disconnected_shapes[1].curve_center_y], outline: true) # => false
shape.contain?(shape.disconnected_shapes[1].curve_center_x + 1, shape.disconnected_shapes[1].curve_center_y, outline: true, distance_tolerance: 1) # => true
shape.contain?([shape.disconnected_shapes[1].curve_center_x + 1, shape.disconnected_shapes[1].curve_center_y], outline: true, distance_tolerance: 1) # => true
PerfectShape::CompositeShapeClass
Extends PerfectShape::Shape
A composite shape is simply an aggregate of multiple shapes (e.g. square and triangle polygon)

::new(shapes: []): constructs a composite shape with shapes as Array of PerfectShape::Shape objects#shapes: the shapes that the composite shape is composed of#min_x: min x#min_y: min y#max_x: max x#max_y: max y#width: width (from min x to max x)#height: height (from min y to max y)#center_point: center point as Array of [center_x, center_y] coordinates#center_x: center x#center_y: center y#bounding_box: bounding box is a rectangle with x = min x, y = min y, and width/height of shape (bounding box only guarantees that the shape is within it, but it might be bigger than the shape)#==(other): Returns true if equal to other or false otherwise#contain?(x_or_point, y=nil, outline: false, distance_tolerance: 0): When outline is false, it checks if point is inside any of the shapes owned by the composite shape. Otherwise, when outline is true, it checks if point is on the outline of any of the shapes owned by the composite shape. distance_tolerance can be used as a fuzz factor when outline is true, for example, to help GUI users mouse-click-select a composite shape from its outline more successfully#intersect?(rectangle): Returns true if intersecting with interior of rectangle or false otherwise. This is useful for GUI optimization checks of whether a shape appears in a GUI viewport rectangle and needs redrawingExample:
require 'perfect-shape'
shapes = []
shapes << PerfectShape::Square.new(x: 120, y: 215, length: 100)
shapes << PerfectShape::Polygon.new(points: [[120, 215], [170, 165], [220, 215]])
shape = PerfectShape::CompositeShape.new(shapes: shapes)
shape.contain?(170, 265) # => true inside square
shape.contain?([170, 265]) # => true inside square
shape.contain?(170, 265, outline: true) # => false
shape.contain?([170, 265], outline: true) # => false
shape.contain?(170, 315, outline: true) # => true
shape.contain?([170, 315], outline: true) # => true
shape.contain?(170, 316, outline: true) # => false
shape.contain?([170, 316], outline: true) # => false
shape.contain?(170, 316, outline: true, distance_tolerance: 1) # => true
shape.contain?([170, 316], outline: true, distance_tolerance: 1) # => true
shape.contain?(170, 190) # => true inside polygon
shape.contain?([170, 190]) # => true inside polygon
shape.contain?(170, 190, outline: true) # => false
shape.contain?([170, 190], outline: true) # => false
shape.contain?(145, 190, outline: true) # => true
shape.contain?([145, 190], outline: true) # => true
shape.contain?(145, 189, outline: true) # => false
shape.contain?([145, 189], outline: true) # => false
shape.contain?(145, 189, outline: true, distance_tolerance: 1) # => true
shape.contain?([145, 189], outline: true, distance_tolerance: 1) # => true
Copyright (c) 2021-2022 Andy Maleh. See LICENSE.txt for further details.
FAQs
Unknown package
We found that perfect-shape demonstrated a not healthy version release cadence and project activity because the last version was released a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Security News
CISA’s 2025 draft SBOM guidance adds new fields like hashes, licenses, and tool metadata to make software inventories more actionable.

Security News
A clarification on our recent research investigating 60 malicious Ruby gems.

Security News
ESLint now supports parallel linting with a new --concurrency flag, delivering major speed gains and closing a 10-year-old feature request.