Product
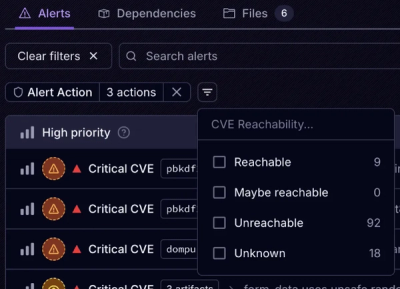
Introducing Tier 1 Reachability: Precision CVE Triage for Enterprise Teams
Socket’s new Tier 1 Reachability filters out up to 80% of irrelevant CVEs, so security teams can focus on the vulnerabilities that matter.
Attitude: orientation of an object in space.
A rotation of the sphere can be represented in various ways, such as:
The attitude module allows conversions and computations between all these representations.
See https://observablehq.com/@fil/attitude for details.
If you use NPM, npm install attitude. Otherwise, download the latest release. AMD, CommonJS, and vanilla environments are supported. In vanilla, an attitude global is exported:
<script src="https://unpkg.com/attitude"></script>
<script>
const attitude = attitude();
</script>
[lambda, phi, gamma], in degrees.
{ axis: [lon, lat], angle: alpha }, in degrees.
[ [r11, r12, r13],
[r21, r22, r23],
[r31, r32, r33] ]
q = [q0, q1, q2, q3, q4] is also called a versor when its norm is equal to 1.
[ x, y, z ] = f(a)B, where f(a) is a scalar encoding the angle, and B a unit vector in cartesian coordinates.
Note: there are many ways to encode the angle, we have to settle on a default. The useful functions f(a) are:
Defaults to the stereographic vector representation.
# attitude([angles])
Returns an attitude object. Sets the rotation’s Euler angles if the angles argument is specified. attitude is equivalent to d3.geoRotation(angles), and can be used as a function to rotate a point [longitude, latitude].
# attitude.invert(point)
Returns the inverse rotation of the point.
# attitude.inverse()
Returns a new attitude, inverse of the original.
# attitude.compose(b)
Returns a new attitude, composition of the original with the argument. When c = a.compose(b) is applied to a point p, the result c(p) = a(b(p)): in other words, the rotation b will be applied first, then rotation a.
# attitude.power(power)
Returns a new partial attitude. a.power(2) is twice the rotation a, a.power(.5) is half the rotation a.
# attitude.arc(A, B)
Returns a new attitude that brings the point A to B by the shortest (geodesic) path.
# attitude.interpolateTo(b)
Returns an interpolator that continuously transitions the original attitude to the argument. The result is a function of t that is equivalent to attitude for t = 0, and equivalent to b for t = 1. Useful for spherical linear interpolation (SLERP).
# attitude.angles([angles])
Sets or reads the Euler angles of an attitude, as an array [φ, λ, γ] (in degrees).
# attitude.axis([axis])
Sets or reads the rotation axis of an attitude, as [lon, lat] coordinates.
# attitude.angle([angle])
Sets or reads the rotation angle of an attitude, in degrees.
# attitude.versor([versor])
Sets or reads the versor representation of an attitude, as a length-4 array.
# attitude.matrix([matrix])
Sets or reads the matrix representation of an attitude, as a matrix of size 3×3.
# attitude.vector([vector])
Sets or reads the vector representation of an attitude, as a length-3 array. That array can be written f(a)B, where f is a function of the rotation’s angle, and B a unit vector respresenting the axis in cartesian coordinates.
Defaults to the stereographic vector: f(a) = tan(a/4).
# attitude.vectorStereographic([vector])
Stereographic vector: f(a) = tan(a/4). Also called the ‘Modified Rodrigues Parameters’.
# attitude.vectorGnomonic([vector])
Gnomonic vector: f(a) = tan(a/2). Also called ‘Rodrigues Parameters’ or ‘Gibbs vector’.
# attitude.vectorEquidistant([vector])
Equidistant vector: f(a) = a. Also called the logarithm vector.
With thanks to Jacob Rus, Nadieh Bremer, Mike Bostock and Darcy Murphy.
FAQs
Spherical Rotations
The npm package attitude receives a total of 30 weekly downloads. As such, attitude popularity was classified as not popular.
We found that attitude demonstrated a not healthy version release cadence and project activity because the last version was released a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Product
Socket’s new Tier 1 Reachability filters out up to 80% of irrelevant CVEs, so security teams can focus on the vulnerabilities that matter.
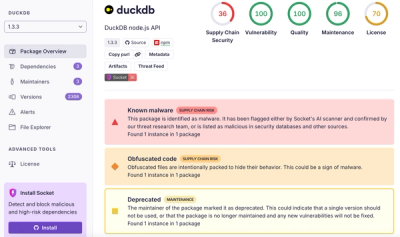
Research
/Security News
Ongoing npm supply chain attack spreads to DuckDB: multiple packages compromised with the same wallet-drainer malware.

Security News
The MCP Steering Committee has launched the official MCP Registry in preview, a central hub for discovering and publishing MCP servers.