Product
Announcing Precomputed Reachability Analysis in Socket
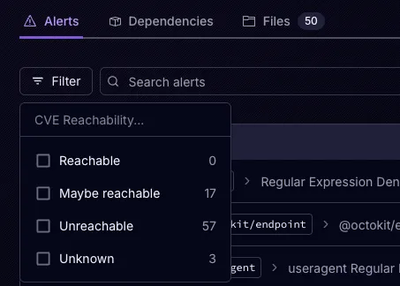
Socket’s precomputed reachability slashes false positives by flagging up to 80% of vulnerabilities as irrelevant, with no setup and instant results.
Python Library for Elliptic Curve Cryptography: key exchanges (Diffie-Hellman, Massey-Omura), ECDSA signatures, and Koblitz encoding. Suitable for crypto education and secure systems.
Python Library for Elliptic Curve Cryptography
Elliptic Curve Utils, or ecutils, is a Python package that provides utilities for working with elliptic curves, particularly in the context of cryptography. It includes functionality for operations like point addition and scalar multiplication on curves, as well as higher-level protocols like key exchange and digital signatures.
You can install the ecutils package using pip:
pip install ecutils
After installing the ecutils library, you can import it into your Python project. Below are the steps for using the library:
# Importing core classes and functions
from ecutils.core import EllipticCurve, Point
from ecutils.curves import get as get_curve
from ecutils.settings import LRU_CACHE_MAXSIZE
# Importing protocols
from ecutils.protocols import DiffieHellman, MasseyOmura
# Importing algorithms
from ecutils.algorithms import Koblitz, DigitalSignature
DigitalSignature__init__(self, private_key, curve_name='secp192k1')
DigitalSignature class for performing ECDSA (Elliptic Curve Digital Signature Algorithm) operations.private_key: The private key used for generating a signature.curve_name: (Optional) The name of the elliptic curve to use. Defaults to 'secp192k1'.public_key
Point representing the public key of the signer.generate_signature(self, message_hash)
message_hash: The hash of the message to be signed (string or bytes).(r: int, s: int) representing the ECDSA signature components.verify_signature(self, public_key, message_hash, r, s)
(r, s) against a public key and a message hash.public_key: The public key associated with the signature.message_hash: The hash of the message that was signed (string or bytes).r: The r component of the signature (int).s: The s component of the signature (int).True if the signature is valid; False otherwise.Koblitz__init__(self, curve_name='secp521r1')
Koblitz class for encoding and decoding messages on elliptic curves using the Koblitz method.curve_name: (Optional) The name of the elliptic curve to use. Defaults to 'secp521r1'.encode(self, message, alphabet_size=256, chunked=False)
message: The string message to be encoded.alphabet_size: (Optional) The size of the character set used in the message. Defaults to 256 (for ASCII).chunked: (Optional) Set to True for encoding large messages in chunks. Defaults to False.(Point, int) representing the encoded message as a point on the curve.decode(self, encoded, j=0, alphabet_size=256, chunked=False)
encoded: The point on the elliptic curve or tuple of points representing the encoded message.j: (Optional) An auxiliary value used during encoding. Defaults to 0.alphabet_size: (Optional) The size of the character set used during encoding. Defaults to 256 (for ASCII).chunked: (Optional) Set to True if the message was encoded in chunks. Defaults to False.DiffieHellman__init__(self, private_key, curve_name='secp192k1')
DiffieHellman class for performing Diffie-Hellman key exchange using elliptic curves.private_key: The private key of the user.curve_name: (Optional) The name of the elliptic curve to use. Defaults to 'secp192k1'.public_key
Point representing the user's public key.compute_shared_secret(self, other_public_key)
other_public_key: The other party's public key.Point.MasseyOmura__init__(self, private_key, curve_name='secp192k1')
MasseyOmura class for performing the Massey-Omura key exchange using elliptic curves.private_key: The private key of the user.curve_name: (Optional) The name of the elliptic curve to use. Defaults to 'secp192k1'.public_key
Point representing the user's public key.first_encryption_step(self, message)
message: The original message as a Point.Point.second_encryption_step(self, received_encrypted_message)
received_encrypted_message: The encrypted message received from the other party.Point.partial_decryption_step(self, encrypted_message)
encrypted_message: The encrypted message as a Point.Point.EllipticCurve__init__(self, p, a, b, G, n, h, use_projective_coordinates=True)
EllipticCurve class to define the elliptic curve parameters and available mathematical operations.p: The prime order of the finite field.a: The coefficient a in the elliptic curve equation.b: The coefficient b in the elliptic curve equation.G: The base point/origin of the curve (point generator).n: The order of the base point.h: The cofactor of the elliptic curve.use_projective_coordinates: (Optional) Whether to use Jacobian/projective coordinate systems for efficient point operations. Defaults to True.add_points(self, p1, p2)
p1 and p2 on the elliptic curve.p1: Point on the elliptic curve.p2: Another point to be added.Point representing the sum of the two points.double_point(self, p)
p: The point on the elliptic curve to be doubled.Point.multiply_point(self, k, p)
k on the elliptic curve.k: The integer scalar to multiply by.p: The point to be multiplied.Point.is_point_on_curve(self, p)
p: The point to check.True if the point is on the curve; False otherwise.For more in-depth use and examples, check out the official documentation.
In the following examples, you'll see how to use ecutils for essential elliptic curve operations and cryptographic protocols, including message encoding, digital signatures with ECDSA, and key exchange methods. These practical implementations will help you quickly integrate elliptic curve cryptography into your applications.
from ecutils.algorithms import Koblitz
# Initialize Koblitz with a specific curve
koblitz = Koblitz(curve_name="secp256k1")
# Encode a message to a curve point
point, j = koblitz.encode("Hello, World!")
# Decode the curve point back to a message
decoded_message = Koblitz.decode(point, j)
from ecutils.algorithms import DigitalSignature
# Create a DigitalSignature instance with your private key
ds = DigitalSignature(private_key=123456)
# Hash of your message
message_hash = hash('your message')
# Generate signature
r, s = ds.generate_signature(message_hash)
# Verify signature (typically on the receiver's side)
is_valid = ds.verify_signature(ds.public_key, message_hash, r, s)
from ecutils.protocols import DiffieHellman
# Alice's side
alice = DiffieHellman(private_key=12345)
# Bob's side
bob = DiffieHellman(private_key=67890)
# Alice computes her shared secret with Bob's public key
alice_shared_secret = alice.compute_shared_secret(bob.public_key)
# Bob computes his shared secret with Alice's public key
bob_shared_secret = bob.compute_shared_secret(alice.public_key)
# alice_shared_secret should be equal to bob_shared_secret
from ecutils.protocols import MasseyOmura
from ecutils.algorithms import Koblitz
# Initialize the Koblitz instance for the elliptic curve 'secp192k1'
koblitz = Koblitz(curve_name='secp192k1')
# Sender's side
# -------------
# Sender chooses their private key
private_key_sender = 123456789
# Initialize Massey-Omura protocol with the sender's private key
mo_sender = MasseyOmura(private_key_sender, curve_name='secp192k1')
# Encode the message using the Koblitz method
# `j` is used to handle the ambiguity in the decoding process
message, j = koblitz.encode("Hello, world!")
# Perform the first encryption step with Massey-Omura protocol
encrypted_msg_sender = mo_sender.first_encryption_step(message)
# The encoded message is now sent to the receiver...
# (transmission of encrypted_msg_sender)
# Receiver's side
# ---------------
# Receiver chooses their private key
private_key_receiver = 987654321
# Initialize Massey-Omura protocol with the receiver's private key
mo_receiver = MasseyOmura(private_key_receiver, curve_name='secp192k1')
# Perform the second encryption step with Massey-Omura protocol
encrypted_msg_receiver = mo_receiver.second_encryption_step(encrypted_msg_sender)
# The double-encrypted message is sent back to the sender...
# (transmission of encrypted_msg_receiver)
# Sender's side again
# -------------------
# Perform the partial decryption step with Massey-Omura protocol
partial_decrypted_msg = mo_sender.partial_decryption_step(encrypted_msg_receiver)
# The partially decrypted message is sent back to the receiver...
# (transmission of partial_decrypted_msg)
# Receiver's final decryption
# ---------------------------
# Finish decryption with Massey-Omura protocol to get the original message
original_message = mo_receiver.partial_decryption_step(partial_decrypted_msg)
# Decode the message using the Koblitz method
# `j` is used to resolve the mapping from the elliptic curve point back to the message
decoded_message = koblitz.decode(original_message, j)
# The decoded_message contains the original plaintext message
print(decoded_message)
For issues, questions, or contributions, please refer to the project's GitHub repository.
This project is licensed under the MIT License.
Don't forget to give this project a star if you find it useful! 🌟
In addition to the Python module, there are other language-specific libraries available for elliptic curve cryptography:
JavaScript Library for Elliptic Curve Cryptography: The js-ecutils package provides elliptic curve functionalities tailored for JavaScript developers. You can find it on GitHub.
Go Library for Elliptic Curve Cryptography: The go-ecutils library offers similar elliptic curve utilities for Go developers. More information and documentation can be found on GitHub.
These libraries enable developers to utilize elliptic curve cryptography in their preferred programming environments, ensuring flexibility and ease of integration.
FAQs
Python Library for Elliptic Curve Cryptography: key exchanges (Diffie-Hellman, Massey-Omura), ECDSA signatures, and Koblitz encoding. Suitable for crypto education and secure systems.
We found that ecutils demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Product
Socket’s precomputed reachability slashes false positives by flagging up to 80% of vulnerabilities as irrelevant, with no setup and instant results.

Product
Socket is launching experimental protection for Chrome extensions, scanning for malware and risky permissions to prevent silent supply chain attacks.

Product
Add secure dependency scanning to Claude Desktop with Socket MCP, a one-click extension that keeps your coding conversations safe from malicious packages.