
Security News
JSR Working Group Kicks Off with Ambitious Roadmap and Plans for Open Governance
At its inaugural meeting, the JSR Working Group outlined plans for an open governance model and a roadmap to enhance JavaScript package management.
avlbinstree
Advanced tools
ES6 implementation of the AVL self-balancing binary search tree data structure with TypeScript support.
Come over to Twitter to share your thoughts on the project.
Visit the contributing guidelines to learn more on how to translate this document into more languages.
yarn add avlbinstree
npm install avlbinstree
An AVL tree is a self-balancing binary search tree data structure, whose nodes contain a unique key, an associated value, and point to two distinguished left and right sub-trees. In the tree, the heights of the two child sub-trees of any node differ by at most one. If during a mutating operation, e.g insertion, deletion, a temporary height difference of more than one arises between two child sub-trees, the balance property of the parent sub-tree, thus of the entire tree itself, is restored through the internal usage of tree rotations. These repair tools move the tree nodes only vertically, so that the horizontal/in-order sequence of their keys is fully preserved. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases, where n is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.
Avlbinstree exposes a chainable API, that can be utilized through a simple and minimal syntax, allowing you to combine methods effectively.
Usage examples can be also found at the test directory.
'use strict';
const {Tree, Node} = require('avlbinstree');
const tree = new Tree();
//=> Tree { root: null }
tree.insert(9, 'A');
// => Tree { root: Node { left: null, right: null, key: 9, value: 'A' } }
tree.root;
//=> Node { left: null, right: null, key: 10, value: 'A' }
const node = new Node(9, 'A');
tree.root.key === node.key;
//=> true
tree.root.value === node.value;
//=> true
tree.insert(5, 'B').insert(13, 'C').root;
//=> Node { left: [Node], right: [Node], key: 9, value: 'A' }
tree.root.left;
//=> Node { left: null, right: null, key: 5, value: 'B' }
tree.root.right;
//=> Node { left: null, right: null, key: 13, value: 'C' }
tree.insert(11, 'D').insert(15, 'E');
/*=> {9}
* / \
* {5} {13}
* / \
* {11} {15}
*/
tree.size();
//=> 5
tree.search(13);
//=> Node { key: 13, value: 'C',
// left: Node { left: null, right: null, key: 11, value: 'D' },
// right: Node { left: null, right: null, key: 15, value: 'E' } }
tree.search(25);
//=> null
tree.includes(11);
//=> true
tree.includes(100);
//=> false
tree.height();
//=> 2
tree.remove(5);
/*=> {13}
* / \
* {9} {15}
* \
* {11}
*/
tree.root.isRightHeavy();
//=> false
tree.root.isLeftHeavy();
//=> true
tree.max();
//=> Node { left: null, right: null, key: 15, value: 'E' }
tree.maxKey();
//=> 15
tree.maxValue();
//=> 'E'
tree.min();
//=> Node { left: null, right: null, key: 9, value: 'A' }
tree.minKey();
//=> 9
tree.minValue();
//=> 'A'
tree.remove(15);
/*=> {11}
* / \
* {9} {13}
*/
tree.root.isBalanced();
//=> true
tree.keys();
//=> [9, 11, 13]
tree.values();
//=> ['A', 'D', 'C']
rootNode | nullReturns the root node of the tree.
If the tree is empty null is returned.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A');
// => Tree { root: Node { key: 10, value: 'A', left: null, right: null } }
tree.root;
// => Node { key: 10, value: 'A', left: null, right: null }
clear()TreeMutates the tree by removing all residing nodes and returns it empty.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(15, 'C');
//=> Tree { root: Node { left: [Node], right: [Node], key: 3, value: 'A' } }
tree.size();
//=> 3
tree.clear();
//=> Tree { root: null } }
tree.size();
//=> 0
fullNodes()Array<Node>Applies in-order traversal to the tree and stores each traversed full node (node with two non-null children) in an array. The array is returned at the end of the traversal.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(15, 'C');
tree.fullNodes();
//=> [
// Node { left: [Node], right: [Node], key: 10, value: 'A' }
// ]
height()NumberReturns the maximum distance of any leaf node from the root.
If the tree is empty -1 is returned.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A');
tree.height();
// => 0
tree.insert(5, 'B').insert(15, 'C').insert(25, 'D');
tree.height();
//=> 3
includes(key)BooleanDetermines whether the tree includes a node with a certain key, returning true or false as appropriate.
keyNumberNode key to search for.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B');
tree.includes(10);
// => true
tree.includes(25);
// => false
tree.includes(5);
// => true
inOrder(fn)TreeApplies in-order traversal (depth-first traversal - LNR) to the tree and executes the provided fn function on each traversed node without mutating the tree itself.
fnFunctionFunction to execute on each node.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(15, 'C');
tree.inOrder(node => console.log(node.key));
// => 5
// 10
// 15
insert(key, value)TreeMutates the tree by inserting a new node at the appropriate location.
keyNumberCan be any number that will correspond to the key of the created node.
Each node has its own unique key.
valueAnyCan be any value that will stored in the created node.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A');
// => Tree { root: Node { key: 10, value: 'A', left: null, right: null } }
internalNodes()Array<Node>Applies in-order traversal to the tree and stores each traversed internal node (node with at least a single non-null child) in an array. The array is returned at the end of the traversal.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(15, 'C').insert(20, 'D');
tree.internalNodes();
//=> [
// Node { left: [Node], right: [Node], key: 10, value: 'A' },
// Node { left: null, right: [Node], key: 15, value: 'C' }
// ]
isComplete()BooleanThe method returns true if the tree is a complete binary search tree, which implies that every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
In any other case, the method returns false.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(15, 'C');
tree.isComplete();
//=> true
tree.insert(3, 'D');
tree.isComplete();
//=> true
tree.insert(20, 'E');
tree.isComplete();
//=> false
isEmpty()BooleanDetermines whether the tree is empty, returning true or false as appropriate.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A');
tree.isEmpty();
// => false
isFull()BooleanThe method returns true if all the nodes residing in the tree are either leaf nodes or full nodes.
In any other case (node degree equal to 1) the method returns false.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(15, 'C');
tree.isFull();
//=> true
tree.insert(8, 'D');
tree.isFull();
//=> false
isPerfect()BooleanThe method returns true if all the internal nodes residing in the tree are full nodes (node degree equal to 2) and all leaf nodes are at the same height level. In any other case (node degree equal to 1 or leaf and full nodes are found on the same height level) the method returns false.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(15, 'C');
tree.isPerfect();
//=> true
tree.insert(3, 'D').insert(7, 'E').insert(12, 'F').insert(20, 'G');
tree.isPerfect();
//=> true
tree.insert(1, 'H');
tree.isPerfect();
//=> false
keys()Array<Number>Applies in-order traversal to the tree and stores the key of each traversed node in an array.
The array is returned at the end of the traversal.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(15, 'C');
tree.keys();
//=> [ 5, 10, 15 ]
leafNodes()Array<Node>Applies in-order traversal to the tree and stores each traversed leaf node (node without children) in an array. The array is returned at the end of the traversal.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(15, 'C');
tree.leafNodes();
//=> [
// Node { left: null, right: null, key: 5, value: 'B' },
// Node { left: null, right: null, key: 15, value: 'C' }
// ]
levelOrder(fn)TreeApplies level-order traversal (breadth-first traversal) to the tree and executes the provided fn function on each traversed node without mutating the tree itself.
fnFunctionFunction to execute on each node.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(15, 'C');
tree.levelOrder(node => console.log(node.key));
// => 10
// 5
// 15
max()Node | nullReturns the right-most node in the tree, thus the node corresponding to the maximum key.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(15, 'B').insert(25, 'C');
tree.max();
// => Node { key: 25, value: 'C', left: null, right: null }
maxKey()Number | nullReturns the key of right-most node in the tree, thus the maximum key in the tree.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(15, 'B').insert(25, 'C');
tree.maxKey();
// => 25
maxValue()Any | nullReturns the value of right-most node in the tree, thus the value of the node corresponding to the maximum key.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(15, 'B').insert(25, 'C');
tree.maxValue();
// => 'C'
min()Node | nullReturns the left-most node in the tree, thus the node corresponding to the minimum key.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(0, 'C');
tree.min();
// => Node { key: 0, value: 'C', left: null, right: null }
minKey()Number | nullReturns the key of the left-most node in the tree, thus the minimum key in the tree.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(15, 'B').insert(25, 'C');
tree.minKey();
// => 10
minValue()Any | nullReturns the value of the left-most node in the tree, thus the value of the node corresponding to the minimum key.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(15, 'B').insert(25, 'C');
tree.maxValue();
// => 'A'
outOrder(fn)TreeApplies out-order traversal (depth-first traversal - RNL) to the tree and executes the provided fn function on each traversed node without mutating the tree itself.
fnFunctionFunction to execute on each node.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(15, 'C');
tree.outOrder(node => console.log(node.key));
// => 15
// 10
// 5
postOrder(fn)TreeApplies post-order traversal (depth-first traversal - LRN) to the tree and executes the provided fn function on each traversed node without mutating the tree itself.
fnFunctionFunction to execute on each node.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(15, 'C');
tree.postOrder(node => console.log(node.key));
// => 5
// 15
// 10
preOrder(fn)TreeApplies pre-order traversal (depth-first traversal - NLR) to the tree and executes the provided fn function on each traversed node without mutating the tree itself.
fnFunctionFunction to execute on each node.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(15, 'C');
tree.preOrder(node => console.log(node.key));
// => 10
// 5
// 15
remove(key)TreeMutates the tree by removing the node corresponding to the key argument.
keyNumberCan be any number that corresponds to the key of an existing node.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A');
tree.remove(10);
//=> Tree { root: null }
search(key)Node | nullDetermines whether the tree includes a node with a certain key, returning the targeted node or null as appropriate.
keyNumberNode key to search for.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B');
tree.search(10);
// => Node { key: 10, value: 'A', left: [Node], right: null }
tree.search(25);
// => null
tree.search(5);
// => Node { key: 5, value: 'B', left: null, right: null }
size()NumberReturns the total number of nodes residing in the tree.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(15, 'B').insert(25, 'C');
tree.size();
// => 3
toArray()Array<Node>Applies in-order traversal to the tree and stores each traversed node in an array. The array is returned at the end of the traversal.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(15, 'C').insert(3, 'D').insert(20, 'F');
tree.toArray();
//=> [
// Node { left: null, right: null, key: 3, value: 'D' },
// Node { left: [Node], right: null, key: 5, value: 'B' },
// Node { left: [Node], right: [Node], key: 10, value: 'A' },
// Node { left: null, right: [Node], key: 15, value: 'C' },
// Node { left: null, right: null, key: 20, value: 'F' }
// ]
toPairs()Array<[Number, Any]>Applies in-order traversal to the tree and for each traversed node stores in an array of size n, where n the size of the tree, an ordered-pair/2-tuple, where the first element is a number corresponding to the key of the traversed node, and the last one is a value of type any, corresponding to the value stored in the traversed node.
The array is returned at the end of the traversal.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(15, 'C').insert(3, 'D').insert(20, 'F');
tree.toPairs();
//=> [ [3, 'D'], [5, 'B'], [10, 'A'], [15, 'C'], [20, 'F'] ]
values()Array<Any>Applies in-order traversal to the tree and stores the value of each traversed node in an array.
The array is returned at the end of the traversal.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(15, 'C');
tree.keys();
//=> [ 'B', 'A', 'C' ]
Also available, along with the Tree exposed class, is the Node class, mainly useful for testing purposes, since it can be utilized to compare tree nodes. The class has a binary constructor method, with a key and a value parameter, corresponding to the key and the value stored in the created instance, respectively.
keyNumberThe key corresponding to the node instance.
const {Node} = require('avlbinstree');
const node = new Node(10, 'A');
// => { key:10, value: 'A', left: null, right: null }
node.key;
//=> 10
valueAnyThe value that the node contains.
const {Node} = require('avlbinstree');
const node = new Node(10, 'A');
// => { key: 10, value: 'A', left: null, right: null }
node.value;
//=> 'A'
node.value = 'B'
// => { key: 10, value: 'B', left: null, right: null }
leftNode | nullThe left sub-tree that the node points to.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').root;
// => { key: 10, value: 'A', left: null, right: null }
tree.root.left;
//=> null
tree.insert(5, 'B').root;
// => { key: 10, value: 'A', left: { key: 5, value: 'B', left: null, right: null } , right: null }
tree.root.left;
//=> { key: 5, value: 'B', left: null, right: null }
rightNode | nullThe right sub-tree that the node points to.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').root;
// => { key: 10, value: 'A', left: null, right: null }
tree.root.right;
//=> null
tree.insert(15, 'B').root;
// => { key: 10, value: 'A', left: null , right: { key: 15, value: 'B', left: null, right: null } }
tree.root.right;
//=> { key: 15, value: 'B', left: null, right: null }
balanceFactorNumberReturns a number corresponding to the balance factor of a node, which is defined as the height difference of its two child sub-trees.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').root.balanceFactor;
//=> 0
tree.insert(5, 'B').root.balanceFactor;
//=> 1
tree.remove(5).insert(15, 'C').root.balanceFactor;
//=> -1
childrenArray<Node>Returns an array contacting the children of the instance, where the left child, if present, is the first element of the array, and the right child, if present, is the last element of the array.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').root.children;
//=> []
tree.insert(5, 'B').insert(15, 'C').root.children;
// => [
// { key: 5, value: 'B', left: null , right: null },
// { key: 15, value: 'C', left: null, right: null }
// ]
degreeNumberReturns the number of sub-trees that the node points to.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').root.degree;
//=> 0
tree.insert(5, 'B').root.degree;
//=> 1
tree.insert(15, 'C').root.degree;
//=> 2
heightNumberReturns the maximum distance of any leaf node from the node instance.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').insert(5, 'B').insert(10, 'C').insert(25, 'D');
tree.root.height;
//=> 2
tree.root.right.height();
//=> 1
isBalanced()BooleanDetermines whether a node is a balanced (has a balance factor equal to 0), returning true or false as appropriate.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').root.isBalanced();
//=> true
tree.insert(5, 'B').root.isBalanced();
//=> false
isFull()BooleanDetermines whether a node is a full node (has two non-null children), returning true or false as appropriate.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').root.isFull();
//=> false
tree.insert(5, 'B').insert(15, 'C').root.isFull();
//=> true
isInternal()BooleanDetermines whether a node is an internal node (has at least one non-null child), returning true or false as appropriate.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').root.isInternal();
//=> false
tree.insert(5, 'B').root.isInternal();
//=> true
isLeaf()BooleanDetermines whether a node is a leaf node (has no children), returning true or false as appropriate.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').root.isLeaf();
//=> true
tree.insert(5, 'B').root.isLeaf();
//=> false
isLeftHeavy()BooleanDetermines whether a node is left heavy (has a balance factor greater than zero), returning true or false as appropriate.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').root.isLeftHeavy();
//=> false
tree.insert(5, 'B').root.isLeftPartial();
//=> true
tree.remove(5).insert(10, 'C').root.isLeftPartial();
//=> false
isLeftPartial()BooleanDetermines whether a node is a left partial node (has ony one left non-null child), returning true or false as appropriate.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').root.isLeftPartial();
//=> false
tree.insert(5, 'B').root.isLeftPartial();
//=> true
isPartial()BooleanDetermines whether a node is a partial node (has ony one non-null child), returning true or false as appropriate.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').root.isPartial();
//=> false
tree.insert(15, 'B').root.isPartial();
//=> true
isRightHeavy()BooleanDetermines whether a node is right heavy (has a balance factor less than zero), returning true or false as appropriate.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').root.isRightHeavy();
//=> false
tree.insert(15, 'C').root.isRightHeavy();
//=> true
tree.remove(15).insert(5, 'B').root.isRightHeavy();
//=> false
isRightPartial()BooleanDetermines whether a node is a right partial node (has ony one right non-null child), returning true or false as appropriate.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').root.isRightPartial();
//=> false
tree.insert(15, 'B').root.isRightPartial();
//=> true
leftChildHeight()NumberReturns the maximum distance of any leaf node from the left child of the parent node instance. If the parent node has no left child, then -1 is returned.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').root.leftChildHeight();
//=> -1
tree.insert(5, 'B').root.leftChildHeight();
//=> 0
maxChildHeight()NumberReturns the maximum between the heights of the two child nodes of parent instance. If the parent node has no children, then -1 is returned.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').root.maxChildHeight();
//=> -1
tree.insert(15, 'B').root.maxChildHeight();
//=> 0
tree.insert(5, 'C').root.maxChildHeight();
//=> 0
tree.insert(1, 'D').root.maxChildHeight();
//=> 1
rightChildHeight()NumberReturns the maximum distance of any leaf node from the right child of the parent node instance. If the parent node has no right child, then -1 is returned.
const {Tree} = require('avlbinstree');
const tree = new Tree();
tree.insert(10, 'A').root.rightChildHeight();
//=> -1
tree.insert(15, 'B').root.rightChildHeight();
//=> 0
toPair()[Number, Any]Returns an ordered-pair/2-tuple, where the first element is a number corresponding to the key of the node, and the last one is a value, that can be of any type, corresponding to the value stored in the node.
const {Node, Tree} = require('avlbinstree');
const tree = new Tree();
const node = new Node(5, 'B');
node.toPair();
//=> [5, 'B']
tree.insert(10, 'A').root.toPair();
//=> [10, 'A']
For more info on how to contribute to the project, please read the contributing guidelines.
cd avlbinstreenpm install or yarn installnpm test or yarn testFAQs
AVL self-balancing binary search trees for ES6
We found that avlbinstree demonstrated a not healthy version release cadence and project activity because the last version was released a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Security News
At its inaugural meeting, the JSR Working Group outlined plans for an open governance model and a roadmap to enhance JavaScript package management.

Security News
Research
An advanced npm supply chain attack is leveraging Ethereum smart contracts for decentralized, persistent malware control, evading traditional defenses.
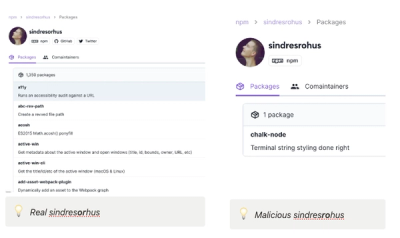
Security News
Research
Attackers are impersonating Sindre Sorhus on npm with a fake 'chalk-node' package containing a malicious backdoor to compromise developers' projects.