garoupa

GaROUPa - Identification based on group theory

The identification module of this library is evolving at its successor library hosh (code) / hosh (package). The algebra module exists only here.

GaROUPa solves the identification problem of multi-valued objects or sequences of events. This Python library / code provides a reference implementation for the UT*.4 specification presented here.

We adopt a novel paradigm to universally unique identification (UUID), making identifiers deterministic and predictable, even before an object is generated by a (possibly costly) process.
Here, data versioning and composition of processing steps are directly mapped as simple operations over identifiers. We call each of the latter a Hosh, i.e., an identifier is an operable hash.

A complete implementation of the remaining ideas from the paper is provided in this cacheable lazy dict which depends on GaROUPa and serves as an advanced usage example.
A more robust (entirely rewritten) version is available in the package idict.

Overview

A product of identifiers produces a new identifier as shown below, where sequences of bytes (b"...") are passed to simulate binary objects to be hashed.

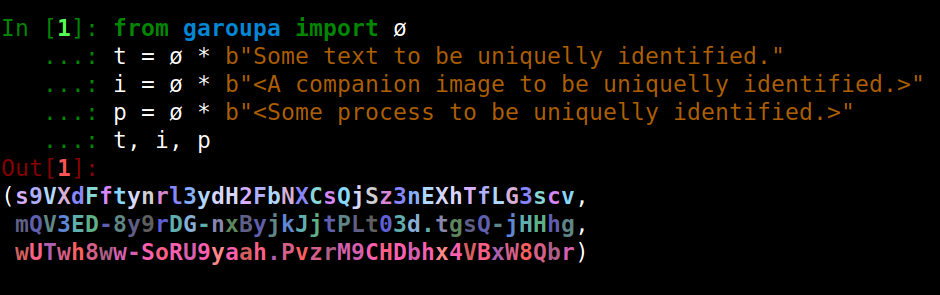	New identifiers are easily created from the identity element ø. Also available as identity for people or systems allergic to utf-8 encoding.

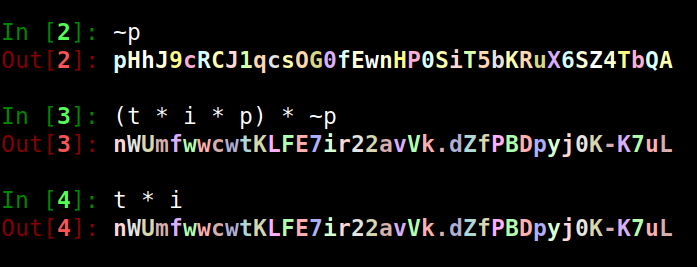	Operations can be reverted by the inverse of the identifier.

	Operations are associative. They are order-sensitive by default, in which case they are called ordered ids.

However, order-insensitive (called unordered) and order-insensitive-among-themselves (called hybrid) identifiers are also available.	.
	.

This is how they affect each other:	.
	.

The chance of collision is determined by the number of possible identifiers of each type. Some versions are provided, e.g.: UT32.4, UT40.4 (default), UT64.4. They can be easily implemented in other languages and are intended to be a specification on how to identify multi-valued objects and multi-step processes. Unordered ids use a very narrow range of the total number of identifiers. This is not a problem as they are not very useful.

One use for unordered ids could be the embedding of authorship or other metadata into an object without worrying about the timing, since the resulting id will remain the same, no matter when the unordered id is operated with the id of the object under construction.	.
	.

Conversely, hybrid ids are excelent to represent values in a data structure like a map, since the order is not relevant when the consumer process looks up for keys, not indexes. Converselly, a chain of a data processing functions usually implies one step is dependent on the result of the previous step. This makes ordered ids the perfect fit to identify functions (and also their composition, as a consequence).

Relationships can also be represented

Here is another possible use. ORCIDs are managed unique identifiers for researchers. They can be directly used as digests to create operable identifiers. We recommend the use of 40 digits to allow operations with SHA-1 hashes. They are common in version control repositories among other uses.

Unordered relationships are represented by hybrid ids. Automatic transparent conversion between ORCID dashes by a hexdecimal character can be implemented in the future if needed.

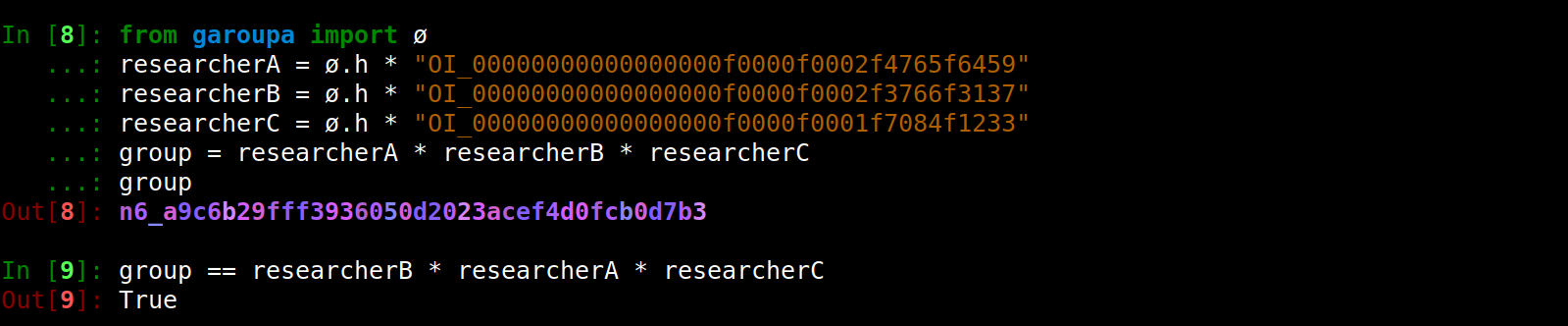
More info

Aside from the paper, PyPI package and GitHub repository, one can find more information, at a higher level application perspective, in this presentation: A lower level perspective is provided in the API documentation.

Python installation

from package

# Set up a virtualenv. 
python3 -m venv venv
source venv/bin/activate

# Install from PyPI
pip install garoupa

from source

git clone https://github.com/davips/garoupa
cd garoupa
poetry install

Examples

Some usage examples.

Basic operations

from garoupa import Hosh, ø  # ø is a shortcut for identity (AltGr+O in most keyboards)

# Hoshes (operable hash-based elements) can be multiplied.
a = Hosh(content=b"Some large binary content...")
b = Hosh(content=b"Some other binary content. Might be, e.g., an action or another large content.")
c = a * b
print(f"{a} * {b} = {c}")
"""
8CG9so9N1nQ59uNO8HGYcZ4ExQW5Haw4mErvw8m8 * 7N-L-10JS-H5DN0-BXW2e5ENWFQFVWswyz39t8s9 = z3EgxfisgqbNXBd0eqDuFiaTblBLA5ZAUbvEZgOh
"""

print(~b)
# Multiplication can be reverted by the inverse hosh. Zero is the identity hosh.
print(f"{b} * {~b} = {b * ~b} = 0")
"""
Q6OjmYZSJ8pB3ogBVMKBOxVp-oZ80czvtUrSyTzS
7N-L-10JS-H5DN0-BXW2e5ENWFQFVWswyz39t8s9 * Q6OjmYZSJ8pB3ogBVMKBOxVp-oZ80czvtUrSyTzS = 0000000000000000000000000000000000000000 = 0
"""

print(f"{b} * {ø} = {b * ø} = b")
"""
7N-L-10JS-H5DN0-BXW2e5ENWFQFVWswyz39t8s9 * 0000000000000000000000000000000000000000 = 7N-L-10JS-H5DN0-BXW2e5ENWFQFVWswyz39t8s9 = b
"""

print(f"{c} * {~b} = {c * ~b} = {a} = a")
"""
z3EgxfisgqbNXBd0eqDuFiaTblBLA5ZAUbvEZgOh * Q6OjmYZSJ8pB3ogBVMKBOxVp-oZ80czvtUrSyTzS = 8CG9so9N1nQ59uNO8HGYcZ4ExQW5Haw4mErvw8m8 = 8CG9so9N1nQ59uNO8HGYcZ4ExQW5Haw4mErvw8m8 = a
"""

print(f"{~a} * {c} = {~a * c} = {b} = b")
"""
RNvSdLI-5RiBBGL8NekctiQofWUIeYvXFP3wvTFT * z3EgxfisgqbNXBd0eqDuFiaTblBLA5ZAUbvEZgOh = 7N-L-10JS-H5DN0-BXW2e5ENWFQFVWswyz39t8s9 = 7N-L-10JS-H5DN0-BXW2e5ENWFQFVWswyz39t8s9 = b
"""

# Division is shorthand for reversion.
print(f"{c} / {b} = {c / b} = a")
"""
z3EgxfisgqbNXBd0eqDuFiaTblBLA5ZAUbvEZgOh / 7N-L-10JS-H5DN0-BXW2e5ENWFQFVWswyz39t8s9 = 8CG9so9N1nQ59uNO8HGYcZ4ExQW5Haw4mErvw8m8 = a
"""

# Hosh multiplication is not expected to be commutative.
print(f"{a * b} != {b * a}")
"""
z3EgxfisgqbNXBd0eqDuFiaTblBLA5ZAUbvEZgOh != wwSd0LaGvuV0W-yEOfgB-yVBMlNLA5ZAUbvEZgOh
"""

# Hosh multiplication is associative.
print(f"{a * (b * c)} = {(a * b) * c}")
"""
RuTcC4ZIr0Y1QLzYmytPRc087a8cbbW9Nj-gXxAz = RuTcC4ZIr0Y1QLzYmytPRc087a8cbbW9Nj-gXxAz
"""

Examples (abstract algebra)

Although not the focus of the library, GaROUPa hosts also some niceties for group theory experimentation. Some examples are provided below.

Abstract algebra module

from itertools import islice
from math import factorial

from garoupa.algebra.cyclic import Z
from garoupa.algebra.dihedral import D
from garoupa.algebra.symmetric import Perm
from garoupa.algebra.symmetric import S

# Direct product between:
#   symmetric group S4;
#   cyclic group Z5; and,
#   dihedral group D4.
G = S(4) * Z(5) * D(4)
print(G)
"""
S4×Z5×D4
"""

# Operating over 5 sampled pairs.
for a, b in islice(zip(G, G), 0, 5):
    print(a, "*", b, "=", a * b, sep="\t")
"""
«[1, 3, 0, 2], 2, ds1»	*	«[2, 0, 3, 1], 0, dr3»	=	«[0, 1, 2, 3], 2, ds2»
«[1, 2, 0, 3], 1, ds0»	*	«[2, 1, 0, 3], 0, ds4»	=	«[0, 2, 1, 3], 1, dr0»
«[3, 2, 0, 1], 3, dr3»	*	«[0, 1, 3, 2], 0, dr5»	=	«[3, 2, 1, 0], 3, dr0»
«[2, 0, 3, 1], 0, dr5»	*	«[1, 0, 3, 2], 1, dr0»	=	«[0, 2, 1, 3], 1, dr1»
«[3, 2, 0, 1], 0, dr7»	*	«[3, 1, 0, 2], 2, dr3»	=	«[1, 2, 3, 0], 2, dr2»
"""

# Operator ~ is another way of sampling.
G = S(12)
print(~G)
"""
[9, 1, 10, 6, 4, 5, 8, 7, 2, 3, 0, 11]
"""

# Manual element creation.
last_perm_i = factorial(12) - 1
a = Perm(i=last_perm_i, n=12)
print("Last element of S35:", a)
"""
Last element of S35: [11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
"""

# Inverse element. Group S4.
a = Perm(i=21, n=4)
b = Perm(i=17, n=4)
print(a, "*", ~a, "=", (a * ~a).i, "=", a * ~a, "= identity")
"""
[1, 3, 2, 0] * [3, 0, 2, 1] = 0 = [0, 1, 2, 3] = identity
"""

print(a, "*", b, "=", a * b)
"""
[1, 3, 2, 0] * [1, 2, 3, 0] = [3, 2, 0, 1]
"""

print(a, "*", b, "*", ~b, "=", a * b * ~b, "= a")
"""
[1, 3, 2, 0] * [1, 2, 3, 0] * [3, 0, 1, 2] = [1, 3, 2, 0] = a
"""

Commutativity degree of groups

from garoupa.algebra.cyclic import Z
from garoupa.algebra.dihedral import D
from garoupa.algebra.matrix.m import M


def traverse(G):
    i, count = G.order, G.order
    for idx, a in enumerate(G.sorted()):
        for b in list(G.sorted())[idx + 1 :]:
            if a * b == b * a:
                count += 2
            i += 2
    print(
        f"|{G}| = ".rjust(20, " "),
        f"{G.order}:".ljust(10, " "),
        f"{count}/{i}:".rjust(15, " "),
        f"  {G.bits} bits",
        f"\t{100 * count / i} %",
        sep="",
    )


# Dihedral
traverse(D(8))
"""
             |D8| = 16:              112/256:  4.0 bits	43.75 %
"""

traverse(D(8) ^ 2)
"""
          |D8×D8| = 256:         12544/65536:  8.0 bits	19.140625 %
"""

# Z4!
traverse(Z(4) * Z(3) * Z(2))
"""
       |Z4×Z3×Z2| = 24:              576/576:  4.584962500721157 bits	100.0 %
"""

# M 3x3 %4
traverse(M(3, 4))

# Large groups (sampling is needed).
Gs = [D(8) ^ 3, D(8) ^ 4, D(8) ^ 5]
for G in Gs:
    i, count = 0, 0
    for a, b in zip(G, G):
        if a * b == b * a:
            count += 1
        if i >= 10_000:
            break
        i += 1
    print(
        f"|{G}| = ".rjust(20, " "),
        f"{G.order}:".ljust(10, " "),
        f"{count}/{i}:".rjust(15, " "),
        f"  {G.bits} bits",
        f"\t~{100 * count / i} %",
        sep="",
    )
"""
           |M3%4| = 64:            2560/4096:  6.0 bits	62.5 %
       |D8×D8×D8| = 4096:          813/10000:  12.0 bits	~8.13 %
    |D8×D8×D8×D8| = 65536:         378/10000:  16.0 bits	~3.78 %
 |D8×D8×D8×D8×D8| = 1048576:       142/10000:  20.0 bits	~1.42 %
"""

Detect identity after many repetitions

import operator
from datetime import datetime
from functools import reduce
from math import log, inf
from sys import argv

from garoupa.algebra.dihedral import D
from garoupa.algebra.symmetric import S

example = len(argv) == 1 or (not argv[1].isdecimal() and argv[1][0] not in ["p", "s", "d"])

primes = [5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107,
          109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229,
          233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359,
          367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491,
          499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641,
          643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787,
          797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941,
          947, 953, 967, 971, 977, 983, 991, 997, 1009]

if example:
    limit, sample = 30, 100
    lst = []  # See *.
    for n in primes[:5]:
        lst.append(D(n, seed=n))
    G = reduce(operator.mul, lst)
else:
    limit, sample = int(argv[2]), int(argv[3]) if len(argv) > 2 else 1_000_000_000_000
    if argv[1] == "s25d":
        G = S(25) * reduce(operator.mul, [D(n) for n in primes[:9]])
    elif argv[1] == "s57":
        G = S(57)
    elif argv[1] == "p384":
        G = reduce(operator.mul, [D(n) for n in primes[:51]])
    elif argv[1] == "p64":
        G = reduce(operator.mul, [D(n) for n in primes[:12]])
    elif argv[1] == "p96":
        G = reduce(operator.mul, [D(n) for n in primes[:16]])
    elif argv[1] == "p128":
        G = reduce(operator.mul, [D(n) for n in primes[:21]])
    elif argv[1] == "p256":
        G = reduce(operator.mul, [D(n) for n in primes[:37]])
    elif argv[1] == "64":
        G = reduce(operator.mul, [D(n) for n in range(5, 31, 2)])
    elif argv[1] == "96":
        G = reduce(operator.mul, [D(n) for n in range(5, 41, 2)])
    elif argv[1] == "128":
        G = reduce(operator.mul, [D(n) for n in range(5, 51, 2)])
    else:
        G = reduce(operator.mul, [D(n) for n in range(5, 86, 2)])

print(f"{G.bits} bits   Pc: {G.comm_degree}  order: {G.order} {G}", flush=True)
print("--------------------------------------------------------------", flush=True)
for hist in G.sampled_orders(sample=sample, limit=limit):
    tot = sum(hist.values())
    bad = 0  # See *.
    for k, v in hist.items():
        if k[0] <= limit:
            bad += v
    print(hist, flush=True)
    hist = hist.copy()
    if (inf, inf) in hist:
        del hist[(inf, inf)]
    hist = {int((k[0] + k[1]) / 2): v for k, v in hist.items()}
    print(
        f"\nbits: {log(G.order, 2):.2f}  Pc: {G.comm_degree or -1:.2e}   a^<{limit}=0: {bad}/{tot} = {bad / tot:.2e}",
        G,
        G._pi_core(hist),
        datetime.now().strftime("%d/%m/%Y %H:%M:%S"),
        flush=True,
    )
# * -> [Explicit FOR due to autogeneration of README through eval]
"""
21.376617194973697 bits   Pc: 0.004113533525298232  order: 2722720 D5×D7×D11×D13×D17
--------------------------------------------------------------
{(-1, 10): 9, (9, 20): 7, (19, 30): 9, (inf, inf): 75}

bits: 21.38  Pc: 4.11e-03   a^<30=0: 25/100 = 2.50e-01 D5×D7×D11×D13×D17 0.125 04/08/2023 18:47:38
"""

Tendence of commutativity on Mn

from itertools import chain

from garoupa.algebra.matrix.m import M
from garoupa.algebra.matrix.m8bit import M8bit


def traverse(G):
    i, count = G.order, G.order
    for idx, a in enumerate(G.sorted()):
        for b in list(G.sorted())[idx + 1:]:
            if a * b == b * a:
                count += 2
            i += 2
    print(f"|{G}| = ".rjust(20, ' '),
          f"{G.order}:".ljust(10, ' '),
          f"{count}/{i}:".rjust(15, ' '), f"  {G.bits} bits",
          f"\t{100 * count / i} %", sep="")


M1_4 = map(M, range(1, 5))
for G in chain(M1_4, [M8bit(), M(5)]):
    traverse(G)
# ...
for G in map(M, range(6, 11)):
    i, count = 0, 0
    for a, b in zip(G, G):
        if a * b == b * a:
            count += 1
        i += 1
        if i >= 1_000_000:
            break
    print(f"|{G}| = ".rjust(20, ' '),
          f"{G.order}:".ljust(10, ' '),
          f"{count}/{i}:".rjust(15, ' '), f"  {G.bits} bits",
          f"\t~{100 * count / i} %", sep="")

"""
|M1| = 1:                        1/1:  0 bits	100.0 %
|M2| = 2:                        4/4:  1 bits	100.0 %
|M3| = 8:                      40/64:  3 bits	62.5 %
|M4| = 64:                 1024/4096:  6 bits	25.0 %
|M8bit| = 256:              14848/65536:  8 bits	22.65625 %
|M5| = 1024:           62464/1048576:  10 bits	5.95703125 %
|M6| = 32768:              286/32768:  15 bits	0.872802734375 %
|M7| = 2097152:          683/1000000:  21 bits	0.0683 %
|M8| = 268435456:         30/1000000:  28 bits	0.003 %
|M9| = 68719476736:        1/1000000:  36 bits	0.0001 %
|M10| = 35184372088832:     0/1000000:  45 bits	0.0 %
"""

Groups benefit from methods from the module 'hosh'

from garoupa.algebra.matrix import M

m = ~M(23)
print(repr(m.hosh))

Performance

Computation time for the simple operations performed by GaROUPa can be considered negligible for most applications, since the order of magnitude of creating and operating identifiers is around a few μs: 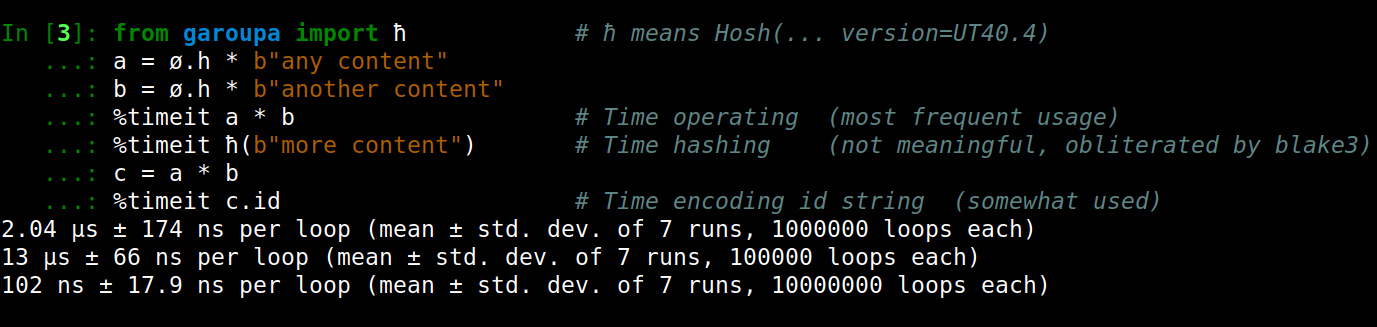On the other hand, we estimate up to ~7x gains in speed when porting the core code to rust. The package hosh was a faster implementation of an earlier version of GaROUPa, It will be updated to be fully compatible with current GaROUPa at major version 2.*.*. As the performance of garoupa seems already very high, an updated 'rust' implementation might become unnecessary. Some parts of the algebra module need additional packages, they can be installed using: poetry install -E full

Grants

This work was partially supported by Fapesp under supervision of Prof. André C. P. L. F. de Carvalho at CEPID-CeMEAI (Grants 2013/07375-0 – 2019/01735-0).