Research
Security News
Malicious npm Package Targets Solana Developers and Hijacks Funds
A malicious npm package targets Solana developers, rerouting funds in 2% of transactions to a hardcoded address.
github.com/schmuio/cryptography
Application-developer-oriented library with commonly applied cryptographic operations.
A compilation of reliable lower level implementations wrapped as developer-friendly higher level API that is safe, has everything in one place and is easy to use.
In our experience with enterprise software we have repeatedly encountered a gap between the developers' need to apply cryptographic operations and the supply of safe and in the meantime easy to use cryptoraphic recipes. Yes, all of it is out there, but getting the entire picture together can take weeks, months or years depending on one's inidividual experience. We went through this journey and now would like to share our work. We intend to continue using this library for our present and future proprietary projects.
We have tried to cover a meaningful variety of cryptographic algorithms which are presently considered industry standard. There are functions for symmetric encryption, asymmetric encryption, digital signatures, time based one time passwords, parallelization resistant hashing and multiple utilities for management of cryptographic keys. One can find both Go native constructs based on the standard crypto library as well as cloud-specific implementations that offer excellent security and key management features. We intend to keep updating the library with additional algorithms and welcome recommendations or feature requests.
Installation:
go get github.com/schmuio/cryptography
Import it in your code and and you are ready to go:
package yourpackage
import (
"github.com/schmuio/cryptography"
)
yourKey, err := cryptography.Key256b()
if err != nil {
// error handling logic
}
ciphertext, err := cryptography.EncryptAesGcm("some-important-plaintext", yourKey)
We have prioritised developer convenience and ability to inspect inputs and outputs visually so most functions are designed to consume string inputs and to provide string outputs. This means that every now and then there are a few type conversions that in a be-as-fast-as-possible scenario can be avoided. This does not mean the functions are not fast, on the contrary - this overhead has a infinitesimal impact compared to the computational cost of the underlying cryptographic operation. Unless you plan to apply these functions in loops with a very high number of iterations or are in a the-fastest-takes-it-all situation, the performance is more than fine. In other words, if you need to measure performance in microseconds or hundreds of nanoseconds - you are fine. If a few nanoseconds per operation are an issue - we recommend that you go for lower level implementations.
For the sake of avoiding repetition we assume that in every example snippet one has already imported the module via adding the following to their code:
package yourpackage
import (
"github.com/schmuio/cryptography"
)
Symmetric encryption algorithms use the same key to encrypt the plaintext and decrypt the respective ciphertext. The library offers the two most widely used algorithms for authenticated symmetric encryption - AES-GCM and ChaCha20-Poly1305 [ 1 ].
Create a key:
yourKey, err := cryptography.Key256b() // Note: alternatively Key128b() can be used
Encrypt:
ciphertext, err := cryptography.EncryptAesGcm("some-important-plaintext", yourKey)
Decrypt:
plaintext, err := cryptography.DecryptAesGcm(ciphertext, yourKey)
Create a key:
yourKey, err := cryptography.KeyChaCha20()
Encrypt:
ciphertext, err := cryptography.EncryptChaCha20("some-important-plaintext", yourKey)
Decrypt:
plaintext, err := cryptography.DecryptChaCha20(ciphertext, yourKey)
⚠ Both algoritms use nonces (numbers-only-used-once) during encryption and reuse of such nonces can have catastrophic consequences (see [ 1 ] for details). In brief, do not use one key for more than 2^32 encryption operations, i.e. rotate the key as frequently as needed so this threshold is not exceeded (see [ 7 ] for an excellent explanation of the problem).
Asymmetric encryption algorithms use one key (referred to as 'public key') to encrypt data and another one (referred to as 'private key') to decrypt them. This is particularly useful in scenarios where many parties should be able to encrypt certain information but there is only one party that is to be allowed to decrypt it. Make sure the private key is always stored securely and do not share it. You can share the public key freely and do not need to treat it as a secret. The library implements the ubiquitous RSA-OAEP algorithm for asymmetric encryption/decryption.
Create a key:
privateKey, publicKey, err := cryptography.RsaKeyPairPem()
Encrypt:
ciphertext, err := cryptography.EncryptRsa("some-important-plaintext", publicKey)
Decrypt:
plaintext, err := cryptography.DecryptRsa(ciphertext, privateKey)
⚠ RSA encryption is not designed to encrypt large messages and the maximim size of the plaintext is restricted by the size of the public key (e.g. 2048 bits) including deductions for padding, etc., details can be found in [ 5 ]. If you need to encrypt longer messages and still rely on an asymmetric encryption workflow a solution is to use hybrid encryption - use a symmetric algorithm for the data and encrypt the symmetric key with an asymmetric algorithm.
Digital signatures are asymmetric cryptography entities that provide proof of the origin of a message and its integrity (i.e. that it comes from the expected source and that it has not been modified). Digital signatures are issued with the private key and are verified with the public key. The private key should be stored securely at all times and should never be shared. The puplic key can be shared with any party that is interested in checking messages signed by the issuer who holds the private key.
Create a key:
privateKey, publicKey, err := cryptography.RsaKeyPairPem()
Sign:
signature, err := cryptography.SignRsaPss("some-very-important-message", privateKeyPem)
Veryfy signature
err = cryptography.VerifyRsaPss("some-very-important-message", signature, publicKeyPem)
privateKey, publicKey, err := cryptography.EcdsaKeyPairHex()
Sign:
signature, err := cryptography.SignEcdsa("some-very-important-message", privateKey)
Veryfy signature
err = cryptography.VerifyEcdsa("some-very-important-message", signature, publicKey)
⚠ It is recomended that RSA-PSS or ECDSA is used whenever possible whereas RSA-PKCS1v15 is also included for cases where compatibility mandades the use of the latter. See [ 1 ] for a detailed review and comparison of digital signatures algorithms.
TOTPs are a highly popular method for adding extra security, e.g. in multi-factor authentication settings. They are derived from the present Unix time and a shared secret provided to an HMAC algorithm. The synchronisation of the Unix time clocks of the client and the server, as well as their shared secret, combined with a deterministic hash algorithm enusure that both parties can derive the same code independently, see details here RFC6238. The library provides a straightforward-to-use API for creating TOTPs and secrets rendered as QR codes so that one can very easily integrate it with 2FA apps like Authy, Google Authenticator, Microsoft Authenticator, etc.
Initial step: create a TotpManager instance with all the necessary data:
secret, err := cryptography.Key512b() // Note: the secret must be of 64-byte size
if err != nil {
// error handling logic
}
tm := cryptography.TotpManager{
Issuer: "yourOrganization",
AccountName: "yourUserEmail@yourOrganization.com",
Algorithm: "SHA1", // Or SHA256, SHA512
Period: 30, // The default period is 30s
Secret: []byte(secret), // Use different secret per every client
}
Generate a TOTP:
totp, err := tm.TOTP() // The result is a string of 6 decimal digits like "123456"
if err != nil {
// error handling logic
}
Validate a TOTP:
isValid, err := tm.Validate(totp)
if err != nil {
// error handling logic
}
Generate QR code:
qrCodeBase64, err := tm.QrCode()
if err != nil {
// error handling logic
}
// Render this QR code (bs64 encoded image) on your UI to allow the user to onboard for 2-factor authentication with an app like Authy, Google Authenticatior, etc.
AES-GCM >> symmetric encryption >> native*
AES-GCM >> symmetric encryption >> via Google Cloud Platform
ChaCha20-Poly1305 >> symmetric encryption >> native
RSA-OAEP >> asymmetric encryption >> native
RSA-OAEP >> asymmetric encryption >> via Google Cloud Platform
RSA-PKCS1v15 >> digital signatures >> native
RSA-PKCS1v15 >> digital signatures >> via Google Cloud Platform
RSA-PSS >> digital signatures >> native
RSA-PSS >> digital signatures >> via Google Cloud Platform
ECDSA p256 >> digital signatures >> native
ECDSA p256/p384/secp256k1 >> digital signatures >> via Google Cloud Platform
RFC 6238 >> time-based one-time passwords >> native
Argon2 >> ASIC resistant key derivation and hashing >> native
*native refers to as locally executable code which does not rely on any external infrastructure
Best effort has been made the code to be covered with meaningful tests. In order the Google Cloud Platform KMS-based encryption tests (and functions) to work, one needs to create keys as described in the GCP documentation - for symmetric encrypt/decrypt, asymmetric encrypt/decrypt and asymmetric sign/verify purposes and set their resource names to the environment variables:
If you intend to use only the native encryption functions please set DISABLE_GCP_TESTS to "1".
At present we plan to maintain this library on our own because it is getting shaped by the needs of the projects we are and will be applying it for. As time is particularly limited, we prefer to not manage this repo as a particularly dynamic one. Nevertheless, we would warmly welcome any remarks, recommendations, feature requests or contribution proposals which we'll review on an individual basis. We commit to fix any bugs and inconsistencies in due course. Please contact us on schmu.io@proton.me on any matter of interest.
[1] Wong, D.(2021).Real-World Cryptography.Manning Publications
[2] Aumasson, J.P.(2017).Serious Cryptography.No Starch Press
[3] https://duo.com/decipher/sha-1-fully-and-practically-broken-by-new-collision
[4] https://eprint.iacr.org/2020/014.pdf
[5] https://mbed-tls.readthedocs.io/en/latest/kb/cryptography/rsa-encryption-maximum-data-size/)
[6] https://csrc.nist.gov/glossary/term/nonce
[7] https://soatok.blog/2020/12/24/cryptographic-wear-out-for-symmetric-encryption/
[8] https://www.ietf.org/rfc/rfc6238.txt
FAQs
Unknown package
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Research
Security News
A malicious npm package targets Solana developers, rerouting funds in 2% of transactions to a hardcoded address.

Security News
Research
Socket researchers have discovered malicious npm packages targeting crypto developers, stealing credentials and wallet data using spyware delivered through typosquats of popular cryptographic libraries.
Security News
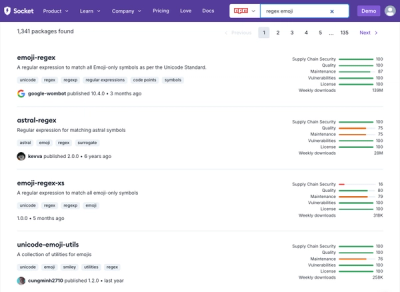
Socket's package search now displays weekly downloads for npm packages, helping developers quickly assess popularity and make more informed decisions.