Research
Security News
Malicious npm Package Targets Solana Developers and Hijacks Funds
A malicious npm package targets Solana developers, rerouting funds in 2% of transactions to a hardcoded address.
@guildofweavers/galois
Advanced tools
Arithmetic and polynomial operations in finite fields.
$ npm install @guildofweavers/galois --save
import * as galois from '@guildofweavers/galois';
// create a prime field with a large modulus
const field = galois.createPrimeField(2n ** 256n - 351n * 2n ** 32n + 1n);
const a = field.rand(); // generate a random field element
const b = field.rand(); // generate another random element
const c = field.exp(a, b); // do some math
You can find complete API definitions in galois.d.ts. Here is a quick overview of the provided functionality:
To perform operations in a finite field, you'll first need to create a FiniteField object. Currently, only prime fields are supported. To create a prime field you can use the createPrimeField function. The function has the following signature:
createPrimeField(modulus: bigint, useWasm?: boolean): FiniteField
Creates a prime field for the specified modulus. If useWasm is set to true, will try to instantiate a WebAssembly-optimized version of the field. If WASM optimization is not available for the specified modulus, will create a regular JavaScript-based field.
createPrimeField(modulus: bigint, wasmOptions: WasmOptions): FiniteField
Tries to create a WebAssembly-optimized prime field for the specified modulus and pass the provided options to it. If WASM optimization is not available for the specified modulus, will create a regular JavaScript-based field.
When provided, wasmOptions object must have the following form:
| Property | Description |
|---|---|
| memory | A WebAssembly Memory object with which the WASM module will be instantiated. |
Once you've created a FiniteField object, you can use the methods described in the following sections to do math.
Vector, matrix, and polynomial operations for certain types of fields have been optimized to make use of WebAssembly. This can speed up such operations by a factor of 6x - 10x (depending on the operation, see performance for more details). The optimization is currently available for the following fields:
Note: there is currently no way to free memory consumed by WASM modules, so, you might have to periodically re-create FiniteField objects to avoid memory leaks. This will be addressed in the future versions of this library by relying on finalizers, which should be available in major JS engines soon.
These methods are self-explanatory. inv computes a multiplicative inverse using the Extended Euclidean algorithm, neg computes an additive inverse.
bigint, b: bigint): bigintbigint, b: bigint): bigintbigint, b: bigint): bigintbigint, b: bigint): bigintbigint, p: bigint): bigintbigint): bigintbigint): bigintVectors are 1-dimensional data structures similar to arrays. Vectors are immutable: once created, their contents cannot be modified. To read values from a vector you can use the following methods:
number): bigintbigint[]Note: for WASM-optimized fields toValues() is a relatively expensive operation since all vector elements have to be copied out of WASM memory into a new JavaScript array.
A FiniteField object exposes two methods which you can use to create new vectors:
newVector(length: number): Vector
Creates a new vector with the specified length (all values initialized to 0).
newVectorFrom(values: bigint[]): Vector
Creates a new vector and populates it with the provided values.
You can also create new vectors by transforming existing vectors using the following methods:
pluckVector(v: Vector, skip: number, times: number): Vector
Creates a new vector by selecting values from the source vector by skipping over the specified number of elements. If skip*times is greater than length of the source vector, the operation will "wrap around" and start plucking from the beginning of the vector.
truncateVector(v: Vector, newLength: number): Vector
Creates a new vector by selecting the number of elements specified by newLength parameter from the head of the source vector.
duplicateVector(v: Vector, times?: number): Vector
Creates a new vector by duplicating the existing vector the specified number of times. For example, duplicating [1, 2] two times will result in [1, 2, 1, 2, 1, 2, 1, 2].
Basic operations can be applied to vectors in the element-wise fashion. For example, addVectorElements computes a new vectors v such that v[i] = a[i] + b[i] for all elements. When the second argument is a scalar, uses that scalar as the second operand in the operation.
addVectorElements(a: Vector, b: bigint | Vector): Vector
subVectorElements(a: Vector, b: bigint | Vector): Vector
mulVectorElements(a: Vector, b: bigint | Vector): Vector
divVectorElements(a: Vector, b: bigint | Vector): Vector
expVectorElements(a: Vector, b: bigint | Vector): Vector
invVectorElements(v: Vector): Vector
Computes multiplicative inverses of all vector elements using Montgomery batch inversion.
negVectorElements(v: Vector): Vector
Computes additive inverses of all vector elements.
Besides the element-wise operations, the following operations can be applied to vectors:
combineVectors(a: Vector, b: Vector): bigint
Computes a linear combination of two vectors.
combineManyVectors(v: Vector[], k: Vector): Vector
Computes linear combinations of vector rows using specified coefficients. For example, v[0][i]*k[0] + v[1][i]*k[1] for all i.
Matrixes are 2-dimensional data structures similar to 2-dimensional arrays. Matrixes are immutable: once created, their contents cannot be modified. Values in matrixes are assumed to be in row-major form. To read values from a matrix you can use the following methods:
number, column: number): bigintbigint[][]Note: for WASM-optimized fields toValues() is a relatively expensive operation since all matrix elements have to be copied out of WASM memory into new JavaScript arrays.
A FiniteField object exposes two methods which you can use to create new matrixes:
newMatrix(rows: number, columns: number): Matrix
Creates a new matrix with the specified number of rows and columns.
newMatrixFrom(values: bigint[][]): Matrix
Creates a new matrix with the same dimensions as values and populates it with the provided values.
You can also create new matrixes by transforming existing vectors using the following methods:
Vector, columns: number): Matrix[1, 2, 3, 4, 5, 6] into a matrix with 2 columns would result in [[1, 3], [2, 5], [3, 6]] matrix.Basic operations can be applied to matrixes in the element-wise fashion. For example, addMatrixElements computes a new matrix m such that m[i][j] = a[i][j] + b[i][j] for all elements. When the second argument is a scalar, uses that scalar as the second operand in the operation.
addMatrixElements(a: Matrix, b: bigint | Matrix): Matrix
subMatrixElements(a: Matrix, b: bigint | Matrix): Matrix
mulMatrixElements(a: Matrix, b: bigint | Matrix): Matrix
divMatrixElements(a: Matrix, b: bigint | Matrix): Matrix
expMatrixElements(a: Matrix, b: bigint | Matrix): Matrix
invMatrixElements(m: Matrix): Matrix
Computes multiplicative inverses of all matrix elements using Montgomery batch inversion.
negMatrixElements(m: Matrix): Matrix
Computes additive inverses of all matrix elements.
Besides the element-wise operations, the following operations can be applied to matrixes:
mulMatrixes(a: Matrix, b: Matrix): Matrix
Computes a product of two matrixes such that given input matrix dimensions [m,p] and [p,n], the output matrix will have dimensions of [m,n].
mulMatrixByVector(m: Matrix, v: Vector): Vector
Similar to matrix multiplication but the second parameter is a vector. Given a matrix with dimensions [m,n] and a vector with length n, the output vector will have length m.
mulMatrixRows(m: Matrix, v: Vector): Matrix
Performs an element-wise multiplication of the vector with each row of the matrix.
matrixRowsToVectors(m: Matrix): Vector[]
Creates an array of vectors corresponding to rows of the source matrix.
Polynomials are Vectors with coefficients of the polynomial encoded in reverse order. For example, a polynomial x^3 + 2x^2 + 3x + 4 would be encoded as [4n, 3n, 2n, 1n].
These methods can be used to perform basic polynomial arithmetic:
Vector, b: Vector): VectorVector, b: Vector): VectorVector, b: Vector): VectorVector, b: Vector): VectorVector, c: bigint): VectorevalPolyAt(p: Vector, x: bigint): bigint
Evaluates a polynomial at the provided x-coordinate.
evalPolyAtRoots(p: Vector, rootsOfUnity: Vector): Vector
Uses Fast Fourier Transform to evaluate polynomials at all provided roots of unity.
evalPolysAtRoots(p: Matrix, rootsOfUnity: Vector): Matrix
Uses Fast Fourier Transform to evaluate polynomials at all provided roots of unity. Each row of the matrix is assumed to be a polynomial, and the result will be a matrix of values.
evalQuarticBatch(polys: Matrix, x: bigint | Vector): Vector
Evaluates a batch of degree 3 polynomials at the provided x coordinate(s). Each row on the poly matrix is assumed to be a polynomial represented by 4 values.
interpolate(xs: Vector, ys: Vector): Vector
Uses Lagrange Interpolation to compute a polynomial from the provided points (x and y coordinates).
interpolateRoots(rootsOfUnity: Vector, ys: Vector | Matrix): Vector | Matrix
Uses Fast Fourier Transform to compute polynomials from the provided points (roots of unity are as x coordinates). If the second parameter is a matrix, each row of the matrix is assumed to be a separate set of y coordinates. In this case, a matrix will be returned with each row representing a separate polynomial.
interpolateQuarticBatch(xSets: Matrix, ySets: Matrix): Matrix
Uses an optimized version of Lagrange Interpolation for degree 3 polynomials. x and y coordinates should be provided in matrixes with 4 values per row.
rand(): bigint
Generate a cryptographically-secure random field element.
prng(seed: bigint | Buffer, length?: number): Vector | bigint
Generates pseudorandom field elements from the provided seed. If the length parameter is provided, a sequence of elements is returned; otherwise, the returned value is a single field element.
getRootOfUnity(order: number): bigint
Computes a primitive root of unity such that root**order = 1.
getPowerSeries(base: bigint, length: number): Vector
Computes a series of powers for the provided base element. More specifically: [1n, base**1, base**2, ..., base**(length - 1)].
Some very informal benchmarks run on Intel Core i5-7300U @ 2.60GHz (single thread). These show approximate number of operations/second:
| Operation | JS BigInt (256-bit) | JS BigInt (128-bit) | WASM (128-bit) |
|---|---|---|---|
| Additions | 3,200,000 | 5,000,000 | 44,000,000 |
| Multiplications | 950,000 | 1,850,000 | 16,300,000 |
| Exponentiations | 3,200 | 10,500 | 97,000 |
MIT © 2019 Guild of Weavers
FAQs
Arithmetic and polynomial operations in finite fields
The npm package @guildofweavers/galois receives a total of 4,465 weekly downloads. As such, @guildofweavers/galois popularity was classified as popular.
We found that @guildofweavers/galois demonstrated a not healthy version release cadence and project activity because the last version was released a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Research
Security News
A malicious npm package targets Solana developers, rerouting funds in 2% of transactions to a hardcoded address.

Security News
Research
Socket researchers have discovered malicious npm packages targeting crypto developers, stealing credentials and wallet data using spyware delivered through typosquats of popular cryptographic libraries.
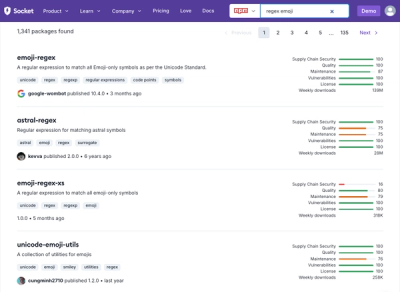
Security News
Socket's package search now displays weekly downloads for npm packages, helping developers quickly assess popularity and make more informed decisions.