bignumber.js

What is bignumber.js?

The bignumber.js package is a JavaScript library for arbitrary-precision decimal and non-decimal arithmetic. It allows for high-precision calculations that are necessary when dealing with very large or very small numbers that cannot be accurately represented with JavaScript's native Number type.

What are bignumber.js's main functionalities?

Arithmetic Operations

Perform precise arithmetic operations such as addition, subtraction, multiplication, and division.

"use strict"; const BigNumber = require('bignumber.js'); let x = new BigNumber(123.4567); let y = new BigNumber('123456.7e-3'); let z = x.plus(y); console.log(z.toString()); // '246.9134'

Chaining Methods

Allows for method chaining to perform multiple operations sequentially on a BigNumber instance.

"use strict"; const BigNumber = require('bignumber.js'); let result = new BigNumber('111.1111111').plus('0.0000001').times('3').sqrt().toPrecision(10); console.log(result); // '1.732050808'

Comparison

Compare two BigNumber instances to determine the relational state.

"use strict"; const BigNumber = require('bignumber.js'); let a = new BigNumber('2'); let b = new BigNumber('3'); console.log(a.isLessThan(b)); // true

Rounding

Round a BigNumber to a specified number of decimal places.

"use strict"; const BigNumber = require('bignumber.js'); let number = new BigNumber('123.4567'); let rounded = number.toFixed(2); console.log(rounded); // '123.46'

Conversion

Convert a BigNumber to a different base or to a string representation.

"use strict"; const BigNumber = require('bignumber.js'); let number = new BigNumber('123456.789e-3'); let inBase10 = number.toString(10); console.log(inBase10); // '123.456789'

Other packages similar to bignumber.js

decimal.js

Similar to bignumber.js, decimal.js is a library for arbitrary-precision Decimal arithmetic. It provides a similar API but focuses strictly on decimal numbers, whereas bignumber.js can handle non-decimal (base 2-36) numbers as well.

big.js

big.js is another arbitrary-precision arithmetic library. It is smaller and simpler than bignumber.js, but it does not include some of the more advanced features and functions that bignumber.js provides.

mathjs

mathjs is an extensive math library for JavaScript and Node.js, which includes functionality for arbitrary-precision arithmetic. It offers a wider range of mathematical functions and data types compared to bignumber.js, but it is also larger in size.

README

A JavaScript library for arbitrary-precision decimal and non-decimal arithmetic.

Features

• Integers and decimals
• Simple API but full-featured
• Faster, smaller, and perhaps easier to use than JavaScript versions of Java's BigDecimal
• 8 KB minified and gzipped
• Replicates the toExponential, toFixed, toPrecision and toString methods of JavaScript's Number type
• Includes a toFraction and a correctly-rounded squareRoot method
• Supports cryptographically-secure pseudo-random number generation
• No dependencies
• Wide platform compatibility: uses JavaScript 1.5 (ECMAScript 3) features only
• Comprehensive documentation and test set

If a smaller and simpler library is required see big.js. It's less than half the size but only works with decimal numbers and only has half the methods. It also does not allow NaN or Infinity, or have the configuration options of this library.

See also decimal.js, which among other things adds support for non-integer powers, and performs all operations to a specified number of significant digits.

Load

The library is the single JavaScript file bignumber.js (or minified, bignumber.min.js).

Browser:

<script src='path/to/bignumber.js'></script>

Node.js:

$ npm install bignumber.js

const BigNumber = require('bignumber.js');

ES6 module:

import BigNumber from "./bignumber.mjs"

AMD loader libraries such as requireJS:

require(['bignumber'], function(BigNumber) {
    // Use BigNumber here in local scope. No global BigNumber.
});

Use

The library exports a single constructor function, BigNumber, which accepts a value of type Number, String or BigNumber,

let x = new BigNumber(123.4567);
let y = BigNumber('123456.7e-3');
let z = new BigNumber(x);
x.isEqualTo(y) && y.isEqualTo(z) && x.isEqualTo(z);      // true

To get the string value of a BigNumber use toString() or toFixed(). Using toFixed() prevents exponential notation being returned, no matter how large or small the value.

let x = new BigNumber('1111222233334444555566');
x.toString();                       // "1.111222233334444555566e+21"
x.toFixed();                        // "1111222233334444555566"

If the limited precision of Number values is not well understood, it is recommended to create BigNumbers from String values rather than Number values to avoid a potential loss of precision.

In all further examples below, let, semicolons and toString calls are not shown. If a commented-out value is in quotes it means toString has been called on the preceding expression.

// Precision loss from using numeric literals with more than 15 significant digits.
new BigNumber(1.0000000000000001)         // '1'
new BigNumber(88259496234518.57)          // '88259496234518.56'
new BigNumber(99999999999999999999)       // '100000000000000000000'

// Precision loss from using numeric literals outside the range of Number values.
new BigNumber(2e+308)                     // 'Infinity'
new BigNumber(1e-324)                     // '0'

// Precision loss from the unexpected result of arithmetic with Number values.
new BigNumber(0.7 + 0.1)                  // '0.7999999999999999'

When creating a BigNumber from a Number, note that a BigNumber is created from a Number's decimal toString() value not from its underlying binary value. If the latter is required, then pass the Number's toString(2) value and specify base 2.

new BigNumber(Number.MAX_VALUE.toString(2), 2)

BigNumbers can be created from values in bases from 2 to 36. See ALPHABET to extend this range.

a = new BigNumber(1011, 2)          // "11"
b = new BigNumber('zz.9', 36)       // "1295.25"
c = a.plus(b)                       // "1306.25"

Performance is better if base 10 is NOT specified for decimal values. Only specify base 10 when it is desired that the number of decimal places of the input value be limited to the current DECIMAL_PLACES setting.

A BigNumber is immutable in the sense that it is not changed by its methods.

0.3 - 0.1                           // 0.19999999999999998
x = new BigNumber(0.3)
x.minus(0.1)                        // "0.2"
x                                   // "0.3"

The methods that return a BigNumber can be chained.

x.dividedBy(y).plus(z).times(9)
x.times('1.23456780123456789e+9').plus(9876.5432321).dividedBy('4444562598.111772').integerValue()

Some of the longer method names have a shorter alias.

x.squareRoot().dividedBy(y).exponentiatedBy(3).isEqualTo(x.sqrt().div(y).pow(3))    // true
x.modulo(y).multipliedBy(z).eq(x.mod(y).times(z))                                   // true

As with JavaScript's Number type, there are toExponential, toFixed and toPrecision methods.

x = new BigNumber(255.5)
x.toExponential(5)                  // "2.55500e+2"
x.toFixed(5)                        // "255.50000"
x.toPrecision(5)                    // "255.50"
x.toNumber()                        //  255.5

A base can be specified for toString. Performance is better if base 10 is NOT specified, i.e. use toString() not toString(10). Only specify base 10 when it is desired that the number of decimal places be limited to the current DECIMAL_PLACES setting.

x.toString(16)                     // "ff.8"

There is a toFormat method which may be useful for internationalisation.

y = new BigNumber('1234567.898765')
y.toFormat(2)                       // "1,234,567.90"

The maximum number of decimal places of the result of an operation involving division (i.e. a division, square root, base conversion or negative power operation) is set using the set or config method of the BigNumber constructor.

The other arithmetic operations always give the exact result.

BigNumber.set({ DECIMAL_PLACES: 10, ROUNDING_MODE: 4 })

x = new BigNumber(2)
y = new BigNumber(3)
z = x.dividedBy(y)                        // "0.6666666667"
z.squareRoot()                            // "0.8164965809"
z.exponentiatedBy(-3)                     // "3.3749999995"
z.toString(2)                             // "0.1010101011"
z.multipliedBy(z)                         // "0.44444444448888888889"
z.multipliedBy(z).decimalPlaces(10)       // "0.4444444445"

There is a toFraction method with an optional maximum denominator argument

y = new BigNumber(355)
pi = y.dividedBy(113)               // "3.1415929204"
pi.toFraction()                     // [ "7853982301", "2500000000" ]
pi.toFraction(1000)                 // [ "355", "113" ]

and isNaN and isFinite methods, as NaN and Infinity are valid BigNumber values.

x = new BigNumber(NaN)                                           // "NaN"
y = new BigNumber(Infinity)                                      // "Infinity"
x.isNaN() && !y.isNaN() && !x.isFinite() && !y.isFinite()        // true

The value of a BigNumber is stored in a decimal floating point format in terms of a coefficient, exponent and sign.

x = new BigNumber(-123.456);
x.c                                 // [ 123, 45600000000000 ]  coefficient (i.e. significand)
x.e                                 // 2                        exponent
x.s                                 // -1                       sign

For advanced usage, multiple BigNumber constructors can be created, each with their own independent configuration.

// Set DECIMAL_PLACES for the original BigNumber constructor
BigNumber.set({ DECIMAL_PLACES: 10 })

// Create another BigNumber constructor, optionally passing in a configuration object
BN = BigNumber.clone({ DECIMAL_PLACES: 5 })

x = new BigNumber(1)
y = new BN(1)

x.div(3)                            // '0.3333333333'
y.div(3)                            // '0.33333'

To avoid having to call toString or valueOf on a BigNumber to get its value in the Node.js REPL or when using console.log use

BigNumber.prototype[require('util').inspect.custom] = BigNumber.prototype.valueOf;

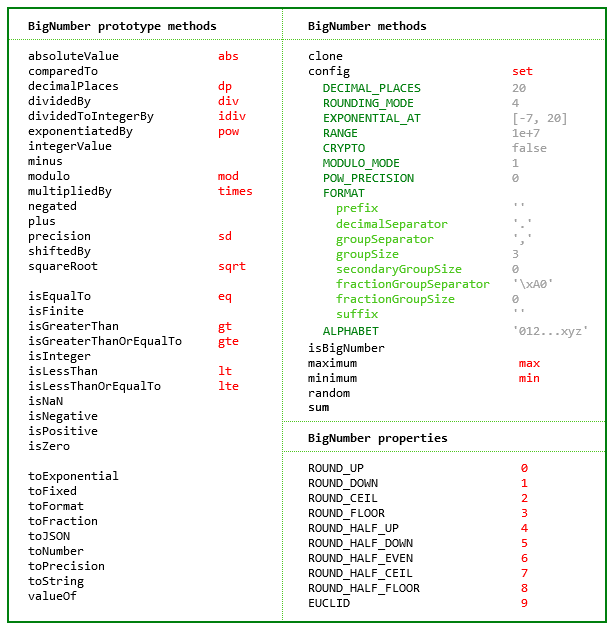
For further information see the API reference in the doc directory.

Test

The test/modules directory contains the test scripts for each method.

The tests can be run with Node.js or a browser. For Node.js use

$ npm test

or

$ node test/test

To test a single method, use, for example

$ node test/methods/toFraction

For the browser, open test/test.html.

Build

For Node, if uglify-js is installed

npm install uglify-js -g

then

npm run build

will create bignumber.min.js.

A source map will also be created in the root directory.

Feedback

Open an issue, or email

Michael

[e-mail]

Licence

The MIT Licence.

See LICENCE.