data-structure-typed

data-structure-typed

Installation and Usage

npm

npm i data-structure-typed --save

yarn

yarn add data-structure-typed

import {
  Heap, Graph, Queue, Deque, PriorityQueue, BST, Trie, DoublyLinkedList,
  AVLTree, SinglyLinkedList, DirectedGraph, RedBlackTree, TreeMultiMap,
  DirectedVertex, Stack, AVLTreeNode
} from 'data-structure-typed';

If you only want to use a specific data structure independently, you can install it separately, for example, by running

npm i heap-typed --save

Why

Do you envy C++ with STL (std::), Python with collections, and Java with java.util ? Well, no need to envy anymore! JavaScript and TypeScript now have data-structure-typed.Benchmark compared with C++ STL. API standards aligned with ES6 and Java. Usability is comparable to Python

Performance

Performance surpasses that of native JS/TS

Method	Time Taken	Data Scale	Belongs To	big O
Queue.push & shift	5.83 ms	100K	Ours	O(1)
Array.push & shift	2829.59 ms	100K	Native JS	O(n)
Deque.unshift & shift	2.44 ms	100K	Ours	O(1)
Array.unshift & shift	4750.37 ms	100K	Native JS	O(n)
HashMap.set	122.51 ms	1M	Ours	O(1)
Map.set	223.80 ms	1M	Native JS	O(1)
Set.add	185.06 ms	1M	Native JS	O(1)

Plain language explanations

Data Structure	Plain Language Definition	Diagram
Linked List (Singly Linked List)	A line of bunnies, where each bunny holds the tail of the bunny in front of it (each bunny only knows the name of the bunny behind it). You want to find a bunny named Pablo, and you have to start searching from the first bunny. If it's not Pablo, you continue following that bunny's tail to the next one. So, you might need to search n times to find Pablo (O(n) time complexity). If you want to insert a bunny named Remi between Pablo and Vicky, it's very simple. You just need to let Vicky release Pablo's tail, let Remi hold Pablo's tail, and then let Vicky hold Remi's tail (O(1) time complexity).
Array	A line of numbered bunnies. If you want to find the bunny named Pablo, you can directly shout out Pablo's number 0680 (finding the element directly through array indexing, O(1) time complexity). However, if you don't know Pablo's number, you still need to search one by one (O(n) time complexity). Moreover, if you want to add a bunny named Vicky behind Pablo, you will need to renumber all the bunnies after Vicky (O(n) time complexity).
Queue	A line of numbered bunnies with a sticky note on the first bunny. For this line with a sticky note on the first bunny, whenever we want to remove a bunny from the front of the line, we only need to move the sticky note to the face of the next bunny without actually removing the bunny to avoid renumbering all the bunnies behind (removing from the front is also O(1) time complexity). For the tail of the line, we don't need to worry because each new bunny added to the tail is directly given a new number (O(1) time complexity) without needing to renumber all the previous bunnies.
Deque	A line of grouped, numbered bunnies with a sticky note on the first bunny. For this line, we manage it by groups. Each time we remove a bunny from the front of the line, we only move the sticky note to the next bunny. This way, we don't need to renumber all the bunnies behind the first bunny each time a bunny is removed. Only when all members of a group are removed do we reassign numbers and regroup. The tail is handled similarly. This is a strategy of delaying and batching operations to offset the drawbacks of the Array data structure that requires moving all elements behind when inserting or deleting elements in the middle.
Doubly Linked List	A line of bunnies where each bunny holds the tail of the bunny in front (each bunny knows the names of the two adjacent bunnies). This provides the Singly Linked List the ability to search forward, and that's all. For example, if you directly come to the bunny Remi in the line and ask her where Vicky is, she will say the one holding my tail behind me, and if you ask her where Pablo is, she will say right in front.
Stack	A line of bunnies in a dead-end tunnel, where bunnies can only be removed from the tunnel entrance (end), and new bunnies can only be added at the entrance (end) as well.
Binary Tree	As the name suggests, it's a tree where each node has at most two children. When you add consecutive data such as [4, 2, 6, 1, 3, 5, 7], it will be a complete binary tree. When you add data like [4, 2, 6, null, 1, 3, null, 5, null, 7], you can specify whether any left or right child node is null, and the shape of the tree is fully controllable.
Binary Search Tree (BST)	A tree-like rabbit colony composed of doubly linked lists where each rabbit has at most two tails. These rabbits are disciplined and obedient, arranged in their positions according to a certain order. The most important data structure in a binary tree (the core is that the time complexity for insertion, deletion, modification, and search is O(log n)). The data stored in a BST is structured and ordered, not in strict order like 1, 2, 3, 4, 5, but maintaining that all nodes in the left subtree are less than the node, and all nodes in the right subtree are greater than the node. This order provides O(log n) time complexity for insertion, deletion, modification, and search. Reducing O(n) to O(log n) is the most common algorithm complexity optimization in the computer field, an exponential improvement in efficiency. It's also the most efficient way to organize unordered data into ordered data (most sorting algorithms only maintain O(n log n)). Of course, the binary search trees we provide support organizing data in both ascending and descending order. Remember that basic BSTs do not have self-balancing capabilities, and if you sequentially add sorted data to this data structure, it will degrade into a list, thus losing the O(log n) capability. Of course, our addMany method is specially handled to prevent degradation. However, for practical applications, please use Red-black Tree or AVL Tree as much as possible, as they inherently have self-balancing functions.
Red-black Tree	A tree-like rabbit colony composed of doubly linked lists, where each rabbit has at most two tails. These rabbits are not only obedient but also intelligent, automatically arranging their positions in a certain order. A self-balancing binary search tree. Each node is marked with a red-black label. Ensuring that no path is more than twice as long as any other (maintaining a certain balance to improve the speed of search, addition, and deletion).
AVL Tree	A tree-like rabbit colony composed of doubly linked lists, where each rabbit has at most two tails. These rabbits are not only obedient but also intelligent, automatically arranging their positions in a certain order, and they follow very strict rules. A self-balancing binary search tree. Each node is marked with a balance factor, representing the height difference between its left and right subtrees. The absolute value of the balance factor does not exceed 1 (maintaining stricter balance, which makes search efficiency higher than Red-black Tree, but insertion and deletion operations will be more complex and relatively less efficient).
Heap	A special type of complete binary tree, often stored in an array, where the children nodes of the node at index i are at indices 2i+1 and 2i+2. Naturally, the parent node of any node is at ⌊(i−1)/2⌋.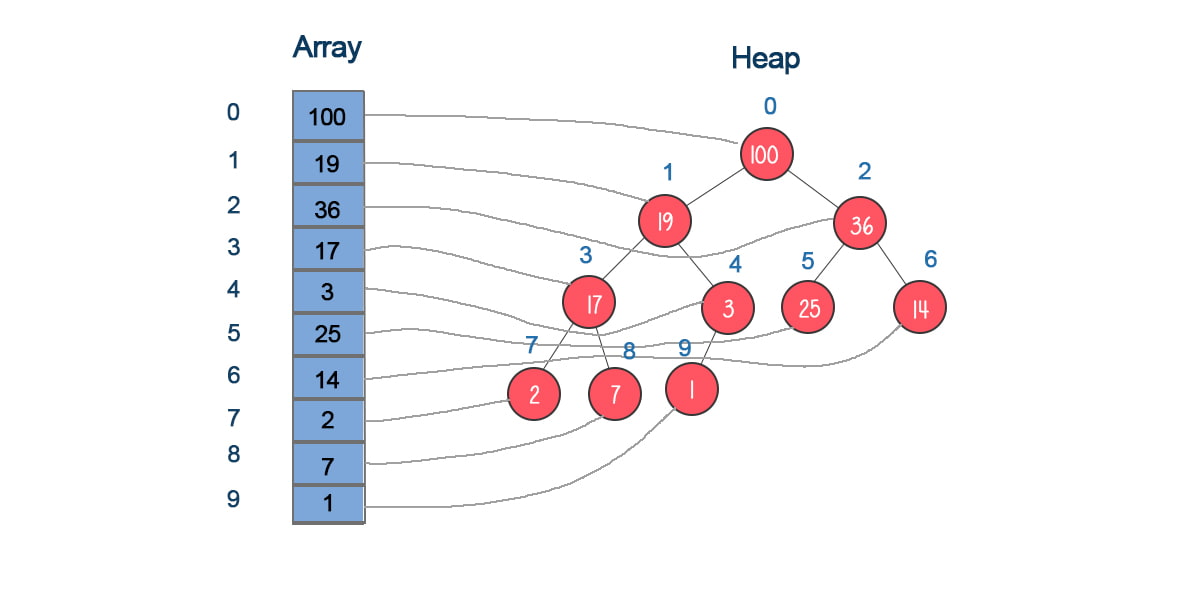
Priority Queue	It's actually a Heap.
Graph	The base class for Directed Graph and Undirected Graph, providing some common methods.
Directed Graph	A network-like bunny group where each bunny can have up to n tails (Singly Linked List).
Undirected Graph	A network-like bunny group where each bunny can have up to n tails (Doubly Linked List).

Conciseness and uniformity

In java.utils, you need to memorize a table for all sequential data structures(Queue, Deque, LinkedList),

Java ArrayList	Java Queue	Java ArrayDeque	Java LinkedList
add	offer	push	push
remove	poll	removeLast	removeLast
remove	poll	removeFirst	removeFirst
add(0, element)	offerFirst	unshift	unshift

whereas in our data-structure-typed, you only need to remember four methods: push, pop, shift, and unshift for all sequential data structures(Queue, Deque, DoublyLinkedList, SinglyLinkedList and Array).

Data structures available

We provide data structures that are not available in JS/TS

Data Structure	Unit Test	Perf Test	API Doc	NPM	Downloads
Binary Tree			Docs	NPM
Binary Search Tree (BST)			Docs	NPM
AVL Tree			Docs	NPM
Red Black Tree			Docs	NPM
Tree Multimap			Docs	NPM
Heap			Docs	NPM
Priority Queue			Docs	NPM
Max Priority Queue			Docs	NPM
Min Priority Queue			Docs	NPM
Trie			Docs	NPM
Graph			Docs	NPM
Directed Graph			Docs	NPM
Undirected Graph			Docs	NPM
Queue			Docs	NPM
Deque			Docs	NPM
Hash Map			Docs
Linked List			Docs	NPM
Singly Linked List			Docs	NPM
Doubly Linked List			Docs	NPM
Stack			Docs	NPM
Segment Tree			Docs
Binary Indexed Tree			Docs

Vivid Examples

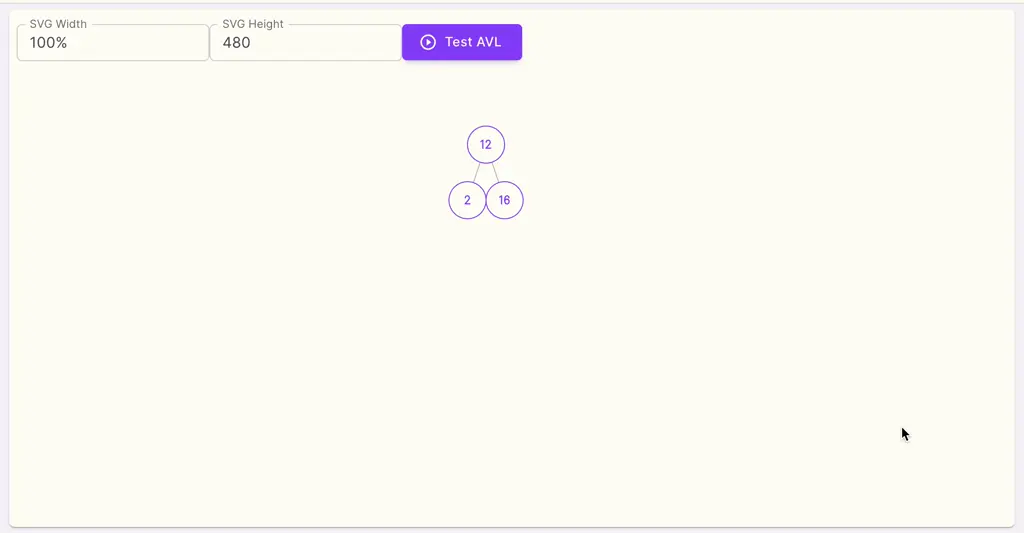
AVL Tree

Try it out, or you can run your own code using our visual tool

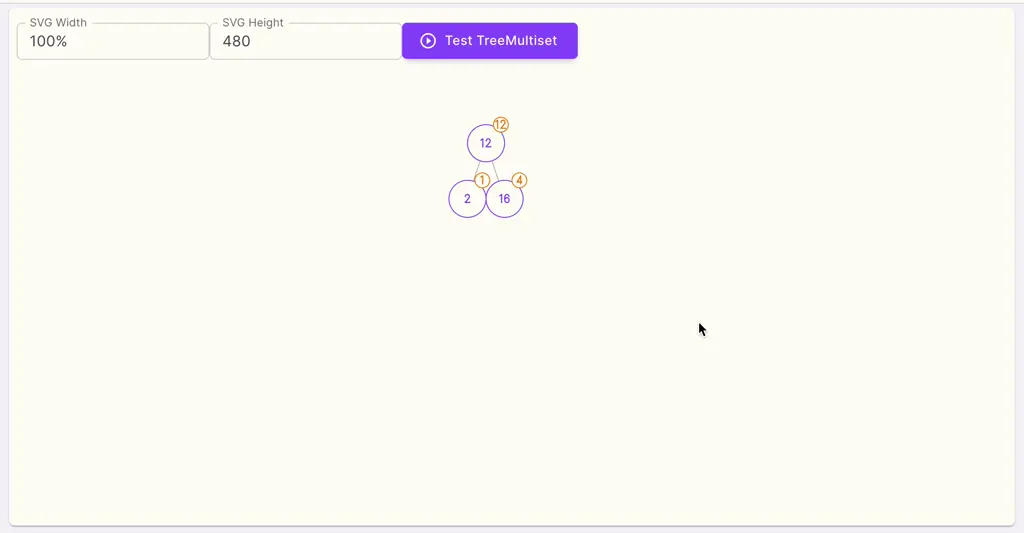
Tree Multi Map

Try it out

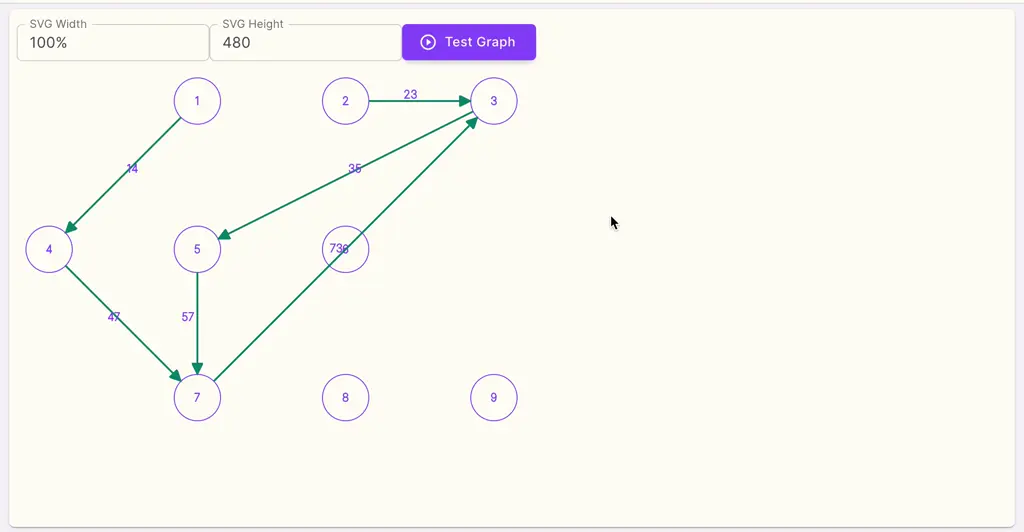
Directed Graph

Try it out

Map Graph

Try it out

Code Snippets

Red Black Tree snippet

TS

import { RedBlackTree } from 'data-structure-typed';

const rbTree = new RedBlackTree<number>();
rbTree.addMany([11, 3, 15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5])
rbTree.isAVLBalanced();    // true
rbTree.delete(10);
rbTree.isAVLBalanced();    // true
rbTree.print()
//         ___6________
//        /            \
//      ___4_       ___11________
//     /     \     /             \
//    _2_    5    _8_       ____14__
//   /   \       /   \     /        \
//   1   3       7   9    12__     15__
//                            \        \
//                           13       16

JS

import { RedBlackTree } from 'data-structure-typed';

const rbTree = new RedBlackTree();
rbTree.addMany([11, 3, 15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5])
rbTree.isAVLBalanced();    // true
rbTree.delete(10);
rbTree.isAVLBalanced();    // true
rbTree.print()
//         ___6________
//        /            \
//      ___4_       ___11________
//     /     \     /             \
//    _2_    5    _8_       ____14__
//   /   \       /   \     /        \
//   1   3       7   9    12__     15__
//                            \        \
//                           13       16

Free conversion between data structures.

const orgArr = [6, 1, 2, 7, 5, 3, 4, 9, 8];
const orgStrArr = ["trie", "trial", "trick", "trip", "tree", "trend", "triangle", "track", "trace", "transmit"];
const entries = [[6, "6"], [1, "1"], [2, "2"], [7, "7"], [5, "5"], [3, "3"], [4, "4"], [9, "9"], [8, "8"]];

const queue = new Queue(orgArr);
queue.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]

const deque = new Deque(orgArr);
deque.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]

const sList = new SinglyLinkedList(orgArr);
sList.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]

const dList = new DoublyLinkedList(orgArr);
dList.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]

const stack = new Stack(orgArr);
stack.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]

const minHeap = new MinHeap(orgArr);
minHeap.print();
// [1, 5, 2, 7, 6, 3, 4, 9, 8]

const maxPQ = new MaxPriorityQueue(orgArr);
maxPQ.print();
// [9, 8, 4, 7, 5, 2, 3, 1, 6]

const biTree = new BinaryTree(entries);
biTree.print();
//         ___6___
//        /       \
//     ___1_     _2_
//    /     \   /   \
//   _7_    5   3   4
//  /   \
//  9   8

const bst = new BST(entries);
bst.print();
//     _____5___
//    /         \
//   _2_       _7_
//  /   \     /   \
//  1   3_    6   8_
//        \         \
//        4         9


const rbTree = new RedBlackTree(entries);
rbTree.print();
//     ___4___
//    /       \
//   _2_     _6___
//  /   \   /     \
//  1   3   5    _8_
//              /   \
//              7   9


const avl = new AVLTree(entries);
avl.print();
//     ___4___
//    /       \
//   _2_     _6___
//  /   \   /     \
//  1   3   5    _8_
//              /   \
//              7   9

const treeMulti = new TreeMultiMap(entries);
treeMulti.print();
//     ___4___
//    /       \
//   _2_     _6___
//  /   \   /     \
//  1   3   5    _8_
//              /   \
//              7   9

const hm = new HashMap(entries);
hm.print()
// [[6, "6"], [1, "1"], [2, "2"], [7, "7"], [5, "5"], [3, "3"], [4, "4"], [9, "9"], [8, "8"]]

const rbTreeH = new RedBlackTree(hm);
rbTreeH.print();
//     ___4___
//    /       \
//   _2_     _6___
//  /   \   /     \
//  1   3   5    _8_
//              /   \
//              7   9

const pq = new MinPriorityQueue(orgArr);
pq.print();
// [1, 5, 2, 7, 6, 3, 4, 9, 8]

const bst1 = new BST(pq);
bst1.print();
//     _____5___
//    /         \
//   _2_       _7_
//  /   \     /   \
//  1   3_    6   8_
//        \         \
//        4         9

const dq1 = new Deque(orgArr);
dq1.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]
const rbTree1 = new RedBlackTree(dq1);
rbTree1.print();
//    _____5___
//   /         \
//  _2___     _7___
// /     \   /     \
// 1    _4   6    _9
//      /         /
//      3         8


const trie2 = new Trie(orgStrArr);
trie2.print();
// ['trie', 'trial', 'triangle', 'trick', 'trip', 'tree', 'trend', 'track', 'trace', 'transmit']
const heap2 = new Heap(trie2, { comparator: (a, b) => Number(a) - Number(b) });
heap2.print();
// ['transmit', 'trace', 'tree', 'trend', 'track', 'trial', 'trip', 'trie', 'trick', 'triangle']
const dq2 = new Deque(heap2);
dq2.print();
// ['transmit', 'trace', 'tree', 'trend', 'track', 'trial', 'trip', 'trie', 'trick', 'triangle']
const entries2 = dq2.map((el, i) => [i, el]);
const avl2 = new AVLTree(entries2);
avl2.print();
//     ___3_______
//    /           \
//   _1_       ___7_
//  /   \     /     \
//  0   2    _5_    8_
//          /   \     \
//          4   6     9

Binary Search Tree (BST) snippet

import { BST, BSTNode } from 'data-structure-typed';

const bst = new BST<number>();
bst.add(11);
bst.add(3);
bst.addMany([15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5]);
bst.size === 16;                // true
bst.has(6);                     // true
const node6 = bst.getNode(6);   // BSTNode
bst.getHeight(6) === 2;         // true
bst.getHeight() === 5;          // true
bst.getDepth(6) === 3;          // true

bst.getLeftMost()?.key === 1;   // true

bst.delete(6);
bst.get(6);                     // undefined
bst.isAVLBalanced();            // true
bst.bfs()[0] === 11;            // true
bst.print()
//       ______________11_____           
//      /                     \          
//   ___3_______            _13_____
//  /           \          /        \    
//  1_     _____8____     12      _15__
//    \   /          \           /     \ 
//    2   4_       _10          14    16
//          \     /                      
//          5_    9
//            \                          
//            7

const objBST = new BST<number, { height: number, age: number }>();

objBST.add(11, { "name": "Pablo", "age": 15 });
objBST.add(3, { "name": "Kirk", "age": 1 });

objBST.addMany([15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5], [
    { "name": "Alice", "age": 15 },
    { "name": "Bob", "age": 1 },
    { "name": "Charlie", "age": 8 },
    { "name": "David", "age": 13 },
    { "name": "Emma", "age": 16 },
    { "name": "Frank", "age": 2 },
    { "name": "Grace", "age": 6 },
    { "name": "Hannah", "age": 9 },
    { "name": "Isaac", "age": 12 },
    { "name": "Jack", "age": 14 },
    { "name": "Katie", "age": 4 },
    { "name": "Liam", "age": 7 },
    { "name": "Mia", "age": 10 },
    { "name": "Noah", "age": 5 }
  ]
);

objBST.delete(11);

AVLTree snippet

import { AVLTree } from 'data-structure-typed';

const avlTree = new AVLTree<number>();
avlTree.addMany([11, 3, 15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5])
avlTree.isAVLBalanced();    // true
avlTree.delete(10);
avlTree.isAVLBalanced();    // true

Directed Graph simple snippet

import { DirectedGraph } from 'data-structure-typed';

const graph = new DirectedGraph<string>();

graph.addVertex('A');
graph.addVertex('B');

graph.hasVertex('A');       // true
graph.hasVertex('B');       // true
graph.hasVertex('C');       // false

graph.addEdge('A', 'B');
graph.hasEdge('A', 'B');    // true
graph.hasEdge('B', 'A');    // false

graph.deleteEdgeSrcToDest('A', 'B');
graph.hasEdge('A', 'B');    // false

graph.addVertex('C');

graph.addEdge('A', 'B');
graph.addEdge('B', 'C');

const topologicalOrderKeys = graph.topologicalSort(); // ['A', 'B', 'C']

Undirected Graph snippet

import { UndirectedGraph } from 'data-structure-typed';

const graph = new UndirectedGraph<string>();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.deleteVertex('C');
graph.addEdge('A', 'B');
graph.addEdge('B', 'D');

const dijkstraResult = graph.dijkstra('A');
Array.from(dijkstraResult?.seen ?? []).map(vertex => vertex.key) // ['A', 'B', 'D']

API docs & Examples

API Docs

Live Examples

Examples Repository

Benchmark

MacBook Pro (15-inch, 2018)

Processor 2.2 GHz 6-Core Intel Core i7

Memory 16 GB 2400 MHz DDR4

Graphics Radeon Pro 555X 4 GB

Intel UHD Graphics 630 1536 MB

macOS Big Sur

Version 11.7.9

heap

test name	time taken (ms)	executions per sec	sample deviation
100,000 add	8.07	123.93	0.00
100,000 add & poll	45.32	22.07	0.01

rb-tree

test name	time taken (ms)	executions per sec	sample deviation
100,000 add	77.03	12.98	0.00
100,000 add randomly	83.26	12.01	0.00
100,000 get	120.25	8.32	0.01
100,000 iterator	26.32	37.99	0.01
100,000 add & delete orderly	161.68	6.19	0.01
100,000 add & delete randomly	268.63	3.72	0.03

queue

test name	time taken (ms)	executions per sec	sample deviation
1,000,000 push	45.55	21.96	0.02
100,000 push & shift	5.54	180.36	0.00
Native JS Array 100,000 push & shift	2467.71	0.41	0.20

deque

test name	time taken (ms)	executions per sec	sample deviation
1,000,000 push	25.36	39.43	0.00
1,000,000 push & pop	32.13	31.12	0.00
1,000,000 push & shift	33.42	29.92	0.00
100,000 push & shift	3.59	278.92	3.21e-4
Native JS Array 100,000 push & shift	2427.03	0.41	0.21
100,000 unshift & shift	3.56	280.81	3.81e-4
Native JS Array 100,000 unshift & shift	4464.18	0.22	0.07

hash-map

test name	time taken (ms)	executions per sec	sample deviation
1,000,000 set	313.05	3.19	0.07
Native JS Map 1,000,000 set	224.48	4.45	0.05
Native JS Set 1,000,000 add	203.46	4.91	0.05
1,000,000 set & get	281.79	3.55	0.07
Native JS Map 1,000,000 set & get	289.57	3.45	0.03
Native JS Set 1,000,000 add & has	195.73	5.11	0.02
1,000,000 ObjKey set & get	348.39	2.87	0.03
Native JS Map 1,000,000 ObjKey set & get	315.23	3.17	0.04
Native JS Set 1,000,000 ObjKey add & has	335.83	2.98	0.06

trie

test name	time taken (ms)	executions per sec	sample deviation
100,000 push	48.09	20.79	0.00
100,000 getWords	93.17	10.73	0.01

avl-tree

test name	time taken (ms)	executions per sec	sample deviation
100,000 add	278.91	3.59	0.01
100,000 add randomly	350.65	2.85	0.02
100,000 get	154.97	6.45	0.03
100,000 iterator	34.78	28.75	0.02
100,000 add & delete orderly	445.45	2.24	0.00
100,000 add & delete randomly	616.61	1.62	0.03

binary-tree-overall

test name	time taken (ms)	executions per sec	sample deviation
10,000 RBTree add randomly	7.07	141.45	7.19e-4
10,000 RBTree get randomly	9.33	107.21	1.48e-4
10,000 RBTree add & delete randomly	18.60	53.77	3.93e-4
10,000 AVLTree add randomly	30.39	32.91	0.01
10,000 AVLTree get randomly	10.70	93.49	0.00
10,000 AVLTree add & delete randomly	46.04	21.72	0.00

directed-graph

test name	time taken (ms)	executions per sec	sample deviation
1,000 addVertex	0.13	7502.53	6.69e-5
1,000 addEdge	7.93	126.13	0.00
1,000 getVertex	0.05	2.19e+4	1.17e-5
1,000 getEdge	18.65	53.61	0.00
tarjan	158.86	6.30	0.01
topologicalSort	141.91	7.05	0.01

doubly-linked-list

test name	time taken (ms)	executions per sec	sample deviation
1,000,000 push	211.26	4.73	0.03
1,000,000 unshift	216.90	4.61	0.07
1,000,000 unshift & shift	208.45	4.80	0.05
1,000,000 addBefore	316.55	3.16	0.06

singly-linked-list

test name	time taken (ms)	executions per sec	sample deviation
1,000,000 push & shift	222.81	4.49	0.08
10,000 push & pop	235.91	4.24	0.01
10,000 addBefore	250.57	3.99	0.01

priority-queue

test name	time taken (ms)	executions per sec	sample deviation
100,000 add	27.64	36.17	8.81e-4
100,000 add & poll	75.52	13.24	9.91e-4

stack

test name	time taken (ms)	executions per sec	sample deviation
1,000,000 push	40.47	24.71	0.01
1,000,000 push & pop	47.47	21.07	0.01

The corresponding relationships between data structures in different language standard libraries.

Data Structure Typed	C++ STL	java.util	Python collections
Heap<E>	-	-	heapq
PriorityQueue<E>	priority_queue<T>	PriorityQueue<E>	-
Deque<E>	deque<T>	ArrayDeque<E>	deque
Queue<E>	queue<T>	Queue<E>	-
HashMap<K, V>	unordered_map<K, V>	HashMap<K, V>	defaultdict
DoublyLinkedList<E>	list<T>	LinkedList<E>	-
SinglyLinkedList<E>	-	-	-
BinaryTree<K, V>	-	-	-
BST<K, V>	-	-	-
RedBlackTree<E>	set<T>	TreeSet<E>	-
RedBlackTree<K, V>	map<K, V>	TreeMap<K, V>	-
TreeMultiMap<K, V>	multimap<K, V>	-	-
TreeMultiMap<E>	multiset<T>	-	-
Trie	-	-	-
DirectedGraph<V, E>	-	-	-
UndirectedGraph<V, E>	-	-	-
PriorityQueue<E>	priority_queue<T>	PriorityQueue<E>	-
Array<E>	vector<T>	ArrayList<E>	list
Stack<E>	stack<T>	Stack<E>	-
HashMap<E>	unordered_set<T>	HashSet<E>	set
-	unordered_multiset	-	Counter
LinkedHashMap<K, V>	-	LinkedHashMap<K, V>	OrderedDict
-	unordered_multimap<K, V>	-	-
-	bitset<N>	-	-

Built-in classic algorithms

Algorithm	Function Description	Iteration Type
Binary Tree DFS	Traverse a binary tree in a depth-first manner, starting from the root node, first visiting the left subtree, and then the right subtree, using recursion.	Recursion + Iteration
Binary Tree BFS	Traverse a binary tree in a breadth-first manner, starting from the root node, visiting nodes level by level from left to right.	Iteration
Graph DFS	Traverse a graph in a depth-first manner, starting from a given node, exploring along one path as deeply as possible, and backtracking to explore other paths. Used for finding connected components, paths, etc.	Recursion + Iteration
Binary Tree Morris	Morris traversal is an in-order traversal algorithm for binary trees with O(1) space complexity. It allows tree traversal without additional stack or recursion.	Iteration
Graph BFS	Traverse a graph in a breadth-first manner, starting from a given node, first visiting nodes directly connected to the starting node, and then expanding level by level. Used for finding shortest paths, etc.	Recursion + Iteration
Graph Tarjan's Algorithm	Find strongly connected components in a graph, typically implemented using depth-first search.	Recursion
Graph Bellman-Ford Algorithm	Finding the shortest paths from a single source, can handle negative weight edges	Iteration
Graph Dijkstra's Algorithm	Finding the shortest paths from a single source, cannot handle negative weight edges	Iteration
Graph Floyd-Warshall Algorithm	Finding the shortest paths between all pairs of nodes	Iteration
Graph getCycles	Find all cycles in a graph or detect the presence of cycles.	Recursion
Graph getCutVertices	Find cut vertices in a graph, which are nodes that, when removed, increase the number of connected components in the graph.	Recursion
Graph getSCCs	Find strongly connected components in a graph, which are subgraphs where any two nodes can reach each other.	Recursion
Graph getBridges	Find bridges in a graph, which are edges that, when removed, increase the number of connected components in the graph.	Recursion
Graph topologicalSort	Perform topological sorting on a directed acyclic graph (DAG) to find a linear order of nodes such that all directed edges go from earlier nodes to later nodes.	Recursion

Software Engineering Design Standards

We strictly adhere to computer science theory and software development standards. Our LinkedList is designed in the traditional sense of the LinkedList data structure, and we refrain from substituting it with a Deque solely for the purpose of showcasing performance test data. However, we have also implemented a Deque based on a dynamic array concurrently.

Principle	Description
Practicality	Follows ES6 and ESNext standards, offering unified and considerate optional parameters, and simplifies method names.
Extensibility	Adheres to OOP (Object-Oriented Programming) principles, allowing inheritance for all data structures.
Modularization	Includes data structure modularization and independent NPM packages.
Efficiency	All methods provide time and space complexity, comparable to native JS performance.
Maintainability	Follows open-source community development standards, complete documentation, continuous integration, and adheres to TDD (Test-Driven Development) patterns.
Testability	Automated and customized unit testing, performance testing, and integration testing.
Portability	Plans for porting to Java, Python, and C++, currently achieved to 80%.
Reusability	Fully decoupled, minimized side effects, and adheres to OOP.
Security	Carefully designed security for member variables and methods. Read-write separation. Data structure software does not need to consider other security aspects.
Scalability	Data structure software does not involve load issues.

supported module system

Now you can use it in Node.js and browser environments

CommonJS:require export.modules =

ESModule:   import export

Typescript:   import export

UMD:           var Deque = dataStructureTyped.Deque

CDN

Copy the line below into the head tag in an HTML document.

development

<script src='https://cdn.jsdelivr.net/npm/data-structure-typed/dist/umd/data-structure-typed.js'></script>

production

<script src='https://cdn.jsdelivr.net/npm/data-structure-typed/dist/umd/data-structure-typed.min.js'></script>

Copy the code below into the script tag of your HTML, and you're good to go with your development.

const { Heap } = dataStructureTyped;
const {
  BinaryTree, Graph, Queue, Stack, PriorityQueue, BST, Trie, DoublyLinkedList,
  AVLTree, MinHeap, SinglyLinkedList, DirectedGraph, TreeMultiMap,
  DirectedVertex, AVLTreeNode
} = dataStructureTyped;

Changelog

v1.52.3 (upcoming)

Changes

• fix(trie): trie returns invalid string when only the fist character m… #94