Security News
The Risks of Misguided Research in Supply Chain Security
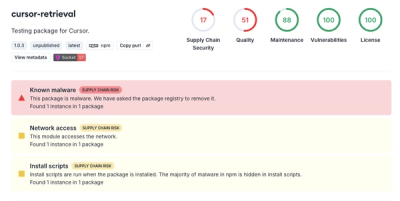
Snyk's use of malicious npm packages for research raises ethical concerns, highlighting risks in public deployment, data exfiltration, and unauthorized testing.
partial.lenses
Advanced tools
Partial lenses is a comprehensive, high-performance optics library for JavaScript



Lenses are basically an abstraction for simultaneously specifying operations to update and query immutable data structures. Lenses are highly composable and can be efficient. This library provides a rich collection of partial isomorphisms, lenses, and traversals, collectively known as optics, for manipulating JSON and users can write new optics for manipulating non-JSON objects, such as Immutable.js collections. A partial lens can view optional data, insert new data, update existing data and remove existing data and can, for example, provide defaults and maintain required data structure parts. Try Lenses!
L.assign(optic, object, maybeData) ~> maybeData v11.13.0L.modify(optic, (maybeValue, index) => maybeValue, maybeData) ~> maybeData v2.2.0L.remove(optic, maybeData) ~> maybeData v2.0.0L.set(optic, maybeValue, maybeData) ~> maybeData v1.0.0L.traverse(algebra, (maybeValue, index) => operation, optic, maybeData) ~> operation v10.0.0L.compose(...optics) ~> optic or [...optics] v1.0.0L.flat(...optics) ~> optic v13.6.0L.choices(optic, ...optics) ~> optic v11.10.0L.choose((maybeValue, index) => optic) ~> optic v1.0.0L.cond(...[(maybeValue, index) => testable, consequentOptic][, [alternativeOptic]]) ~> optic v13.1.0L.condOf(lens, ...[(maybeValue, index) => testable, consequentOptic][, [alternativeOptic]]) ~> optic v13.5.0L.ifElse((maybeValue, index) => testable, optic, optic) ~> optic v13.1.0L.iftes((maybeValue, index) => testable, consequentOptic, ...[, alternativeOptic]) ~> optic v11.14.0L.orElse(backupOptic, primaryOptic) ~> optic v2.1.0L.log(...labels) ~> optic v3.2.0L.Constant ~> Functor v13.7.0L.Identity ~> Monad v13.7.0L.toFunction(optic) ~> optic v7.0.0L.children ~> traversal v13.3.0L.elems ~> traversal v7.3.0L.elemsTotal ~> traversal v13.11.0L.entries ~> traversal v11.21.0L.flatten ~> traversal v11.16.0L.keys ~> traversal v11.21.0L.leafs ~> traversal v13.3.0L.matches(/.../g) ~> traversal v10.4.0L.query(...traversals) ~> traversal v13.6.0L.satisfying((maybeValue, index) => testable) ~> traversal v13.3.0L.values ~> traversal v7.3.0L.all((maybeValue, index) => testable, traversal, maybeData) ~> boolean v9.6.0L.and(traversal, maybeData) ~> boolean v9.6.0L.any((maybeValue, index) => testable, traversal, maybeData) ~> boolean v9.6.0L.collect(traversal, maybeData) ~> [...values] v3.6.0L.collectAs((maybeValue, index) => maybeValue, traversal, maybeData) ~> [...values] v7.2.0L.concat(monoid, traversal, maybeData) ~> value v7.2.0L.concatAs((maybeValue, index) => value, monoid, traversal, maybeData) ~> value v7.2.0L.count(traversal, maybeData) ~> number v9.7.0L.countIf((maybeValue, index) => testable, traversal, maybeData) ~> number v11.2.0L.counts(traversal, maybeData) ~> map v11.21.0L.countsAs((maybeValue, index) => any, traversal, maybeData) ~> map v11.21.0L.foldl((value, maybeValue, index) => value, value, traversal, maybeData) ~> value v7.2.0L.foldr((value, maybeValue, index) => value, value, traversal, maybeData) ~> value v7.2.0L.forEach((maybeValue, index) => undefined, traversal, maybeData) ~> undefined v11.20.0L.forEachWith(() => context, (context, maybeValue, index) => undefined, traversal, maybeData) ~> context v13.4.0L.isDefined(traversal, maybeData) ~> boolean v11.8.0L.isEmpty(traversal, maybeData) ~> boolean v11.5.0L.join(string, traversal, maybeData) ~> string v11.2.0L.joinAs((maybeValue, index) => maybeString, string, traversal, maybeData) ~> string v11.2.0L.maximum(traversal, maybeData) ~> maybeValue v7.2.0L.maximumBy((maybeValue, index) => maybeKey, traversal, maybeData) ~> maybeValue v11.2.0L.mean(traversal, maybeData) ~> number v11.17.0L.meanAs((maybeValue, index) => maybeNumber, traversal, maybeData) ~> number v11.17.0L.minimum(traversal, maybeData) ~> maybeValue v7.2.0L.minimumBy((maybeValue, index) => maybeKey, traversal, maybeData) ~> maybeValue v11.2.0L.none((maybeValue, index) => testable, traversal, maybeData) ~> boolean v11.6.0L.or(traversal, maybeData) ~> boolean v9.6.0L.product(traversal, maybeData) ~> number v7.2.0L.productAs((maybeValue, index) => number, traversal, maybeData) ~> number v11.2.0L.select(traversal, maybeData) ~> maybeValue v9.8.0L.selectAs((maybeValue, index) => maybeValue, traversal, maybeData) ~> maybeValue v9.8.0L.sum(traversal, maybeData) ~> number v7.2.0L.sumAs((maybeValue, index) => number, traversal, maybeData) ~> number v11.2.0L.append ~> lens v1.0.0L.filter((maybeValue, index) => testable) ~> lens v1.0.0L.find((maybeValue, index, {hint: index}) => testable[, {hint: index}]) ~> lens v1.0.0L.findWith(optic[, {hint: index}]) ~> optic v1.0.0L.first ~> lens v13.1.0L.index(elemIndex) ~> lens or elemIndex v1.0.0L.last ~> lens v9.8.0L.prefix(maybeBegin) ~> lens v11.12.0L.slice(maybeBegin, maybeEnd) ~> lens v8.1.0L.suffix(maybeEnd) ~> lens v11.12.0L.pickIn({prop: lens, ...props}) ~> lens v11.11.0L.prop(propName) ~> lens or propName v1.0.0L.props(...propNames) ~> lens v1.4.0L.propsOf(object) ~> lens v11.13.0L.removable(...propNames) ~> lens v9.2.0L.matches(/.../) ~> lens v10.4.0L.valueOr(valueOut) ~> lens v3.5.0L.complement ~> isomorphism v9.7.0L.identity ~> isomorphism v1.3.0L.indexed ~> isomorphism v11.21.0L.is(value) ~> isomorphism v11.1.0L.keyed ~> isomorphism v11.21.0L.reverse ~> isomorphism v11.22.0L.singleton ~> isomorphism v11.18.0L.add(number) ~> isomorphism v13.9.0L.divide(number) ~> isomorphism v13.9.0L.multiply(number) ~> isomorphism v13.9.0L.negate ~> isomorphism v13.9.0L.subtract(number) ~> isomorphism v13.9.0L.pointer(jsonPointer) ~> lens v11.21.0Let's look at an example that is based on an actual early use case that lead to
the development of this library. What we have is an external HTTP API that both
produces and consumes JSON objects that include, among many other properties, a
titles property:
const sampleTitles = {titles: [{language: 'en', text: 'Title'},
{language: 'sv', text: 'Rubrik'}]}
We ultimately want to present the user with a rich enough editor, with features
such as undo-redo and validation, for manipulating the content represented by
those JSON objects. The titles property is really just one tiny part of the
data model, but, in this tutorial, we only look at it, because it is sufficient
for introducing most of the basic ideas.
So, what we'd like to have is a way to access the text of titles in a given
language. Given a language, we want to be able to
Furthermore, when updating, inserting, and removing texts, we'd like the operations to treat the JSON as immutable and create new JSON objects with the changes rather than mutate existing JSON objects, because this makes it trivial to support features such as undo-redo and can also help to avoid bugs associated with mutable state.
Operations like these are what lenses are good at. Lenses can be seen as a
simple embedded DSL
for specifying data manipulation and querying functions. Lenses allow you to
focus on an element in a data structure by specifying a path from the root of
the data structure to the desired element. Given a lens, one can then perform
operations, like get and set, on the element that the
lens focuses on.
Let's first import the libraries
import * as L from 'partial.lenses'
import * as R from 'ramda'
and ▶ play just a bit with lenses.
Note that links with the ▶ play symbol, take you to an interactive version of this page where almost all of the code snippets are editable and evaluated in the browser. There is also a separate playground page that allows you to quickly try out lenses.
As mentioned earlier, with lenses we can specify a path to focus on an element.
To specify such a path we use primitive lenses like
L.prop(propName), to access a named property of an object, and
L.index(elemIndex), to access an element at a given index in an
array, and compose the path using L.compose(...lenses).
So, to just get at the titles array of the sampleTitles we can use
the lens L.prop('titles'):
L.get(L.prop('titles'),
sampleTitles)
// [{ language: 'en', text: 'Title' },
// { language: 'sv', text: 'Rubrik' }]
To focus on the first element of the titles array, we compose with
the L.index(0) lens:
L.get(L.compose(L.prop('titles'),
L.index(0)),
sampleTitles)
// { language: 'en', text: 'Title' }
Then, to focus on the text, we compose with L.prop('text'):
L.get(L.compose(L.prop('titles'),
L.index(0),
L.prop('text')),
sampleTitles)
// 'Title'
We can then use the same composed lens to also set the text:
L.set(L.compose(L.prop('titles'),
L.index(0),
L.prop('text')),
'New title',
sampleTitles)
// { titles: [{ language: 'en', text: 'New title' },
// { language: 'sv', text: 'Rubrik' }] }
In practise, specifying ad hoc lenses like this is not very useful. We'd like to access a text in a given language, so we want a lens parameterized by a given language. To create a parameterized lens, we can write a function that returns a lens. Such a lens should then find the title in the desired language.
Furthermore, while a simple path lens like above allows one to get and set an existing text, it doesn't know enough about the data structure to be able to properly insert new and remove existing texts. So, we will also need to specify such details along with the path to focus on.
Let's then just compose a parameterized lens for accessing the
text of titles:
const textIn = language => L.compose(L.prop('titles'),
L.normalize(R.sortBy(L.get('language'))),
L.find(R.whereEq({language})),
L.valueOr({language, text: ''}),
L.removable('text'),
L.prop('text'))
Take a moment to read through the above definition line by line. Each part
either specifies a step in the path to select the desired element or a way in
which the data structure must be treated at that point. The
L.prop(...) parts are already familiar. The other parts we will
mention below.
Thanks to the parameterized search part,
L.find(R.whereEq({language})), of the lens composition, we can use
it to query titles:
L.get(textIn('sv'), sampleTitles)
// 'Rubrik'
The L.find lens is given a predicate that it then uses to find an
element from an array to focus on. In this case the predicate is specified with
the help of Ramda's R.whereEq function
that creates an equality predicate from a given template object.
Partial lenses can generally deal with missing data. In this case, when
L.find doesn't find an element, it instead works like a lens to
append a new element into an array.
So, if we use the partial lens to query a title that does not exist, we get the default:
L.get(textIn('fi'), sampleTitles)
// ''
We get this value, rather than undefined, thanks to the L.valueOr({language, text: ''}) part of our lens composition, which ensures that we get
the specified value rather than null or undefined. We get the default even
if we query from undefined:
L.get(textIn('fi'), undefined)
// ''
With partial lenses, undefined is the equivalent of non-existent.
As with ordinary lenses, we can use the same lens to update titles:
L.set(textIn('en'), 'The title', sampleTitles)
// { titles: [ { language: 'en', text: 'The title' },
// { language: 'sv', text: 'Rubrik' } ] }
The same partial lens also allows us to insert new titles:
L.set(textIn('fi'), 'Otsikko', sampleTitles)
// { titles: [ { language: 'en', text: 'Title' },
// { language: 'fi', text: 'Otsikko' },
// { language: 'sv', text: 'Rubrik' } ] }
There are a couple of things here that require attention.
The reason that the newly inserted object not only has the text property, but
also the language property is due to the L.valueOr({language, text: ''}) part that we used to provide a default.
Also note the position into which the new title was inserted. The array of
titles is kept sorted thanks to the
L.normalize(R.sortBy(L.get('language'))) part of our lens.
The L.normalize lens transforms the data when either read or
written with the given function. In this case we used Ramda's
R.sortBy to specify that we want the titles
to be kept sorted by language.
Finally, we can use the same partial lens to remove titles:
L.set(textIn('sv'), undefined, sampleTitles)
// { titles: [ { language: 'en', text: 'Title' } ] }
Note that a single title text is actually a part of an object. The key to
having the whole object vanish, rather than just the text property, is the
L.removable('text') part of our lens composition. It makes it
so that when the text property is set to undefined, the result will be
undefined rather than merely an object without the text property.
If we remove all of the titles, we get an empty array:
L.set(L.seq(textIn('sv'),
textIn('en')),
undefined,
sampleTitles)
// { titles: [] }
Above we use L.seq to run the L.set operation over both
of the focused titles.
Take out one (or more) L.normalize(...),
L.valueOr(...) or L.removable(...) part(s)
from the lens composition and try to predict what happens when you rerun the
examples with the modified lens composition. Verify your reasoning by actually
rerunning the examples.
For clarity, the previous code snippets avoided some of the shorthands that this library supports. In particular,
L.compose(...) can be abbreviated as an array
[...],L.prop(propName) can be abbreviated as propName, andL.set(l, undefined, s) can be abbreviated as L.remove(l, s).It is also typical to compose lenses out of short paths following the schema of the JSON data being manipulated. Recall the lens from the start of the example:
L.compose(L.prop('titles'),
L.normalize(R.sortBy(L.get('language'))),
L.find(R.whereEq({language})),
L.valueOr({language, text: ''}),
L.removable('text'),
L.prop('text'))
Following the structure or schema of the JSON, we could break this into three separate lenses:
Furthermore, we could organize the lenses to reflect the structure of the JSON model:
const Title = {
text: [L.removable('text'), 'text']
}
const Titles = {
titleIn: language => [L.find(R.whereEq({language})),
L.valueOr({language, text: ''})]
}
const Model = {
titles: ['titles',
L.normalize(R.sortBy(L.get('language')))],
textIn: language => [Model.titles,
Titles.titleIn(language),
Title.text]
}
We can now say:
L.get(Model.textIn('sv'), sampleTitles)
// 'Rubrik'
This style of organizing lenses is overkill for our toy example. In a more
realistic case the sampleTitles object would contain many more properties.
Also, rather than composing a lens, like Model.textIn above, to access a leaf
property from the root of our object, we might actually compose lenses
incrementally as we inspect the model structure.
So far we have used a lens to manipulate individual items. This library also supports traversals that compose with lenses and can target multiple items. Continuing on the tutorial example, let's define a traversal that targets all the texts:
const texts = [Model.titles,
L.elems,
Title.text]
What makes the above a traversal is the L.elems part. The result
of composing a traversal with a lens is a traversal. The other parts of the
above composition should already be familiar from previous examples. Note how
we were able to use the previously defined Model.titles and Title.text
lenses.
Now, we can use the above traversal to collect all the texts:
L.collect(texts, sampleTitles)
// [ 'Title', 'Rubrik' ]
More generally, we can map and fold over texts. For example, we
could use L.maximumBy to find a title with the maximum length:
L.maximumBy(R.length, texts, sampleTitles)
// 'Rubrik'
Of course, we can also modify texts. For example, we could uppercase all the titles:
L.modify(texts, R.toUpper, sampleTitles)
// { titles: [ { language: 'en', text: 'TITLE' },
// { language: 'sv', text: 'RUBRIK' } ] }
We can also manipulate texts selectively. For example, we could remove all the texts that are longer than 5 characters:
L.remove([texts, L.when(t => t.length > 5)],
sampleTitles)
// { titles: [ { language: 'en', text: 'Title' } ] }
This concludes the tutorial. The reference documentation contains lots of tiny examples and a few more involved examples. The examples section describes a couple of lens compositions we've found practical as well as examples that may help to see possibilities beyond the immediately obvious. The wiki contains further examples and playground links. There is also a document that describes a simplified implementation of optics in a similar style as the implementation of this library. Last, but perhaps not least, there is also a page of Partial Lenses Exercises to solve.
Optics provide a way to decouple the operation to perform on an element or elements of a data structure from the details of selecting the element or elements and the details of maintaining the integrity of the data structure. In other words, a selection algorithm and data structure invariant maintenance can be expressed as a composition of optics and used with many different operations.
Consider how one might approach the tutorial problem without
optics. One could, for example, write a collection of operations like
getText, setText, addText, and remText:
const getEntry = R.curry((language, data) =>
data.titles.find(R.whereEq({language})))
const hasText = R.pipe(getEntry, Boolean)
const getText = R.pipe(getEntry, R.defaultTo({}), R.prop('text'))
const mapProp = R.curry((fn, prop, obj) =>
R.assoc(prop, fn(R.prop(prop, obj)), obj))
const mapText = R.curry((language, fn, data) =>
mapProp(R.map(R.ifElse(R.whereEq({language}),
mapProp(fn, 'text'),
R.identity)),
'titles',
data))
const remText = R.curry((language, data) =>
mapProp(R.filter(R.complement(R.whereEq({language}))),
'titles'))
const addText = R.curry((language, text, data) =>
mapProp(R.append({language, text}), 'titles', data))
const setText = R.curry((language, text, data) =>
mapText(language, R.always(text), data))
You can definitely make the above operations both cleaner and more robust. For
example, consider maintaining the ordering of texts and the handling of cases
such as using addText when there already is a text in the specified language
and setText when there isn't. With partial optics, however, you separate the
selection and data structure invariant maintenance from the operations as
illustrated in the tutorial and due to the separation of concerns
that tends to give you a lot of robust functionality in a small amount of
code.
The combinators provided by this library are available as named imports. Typically one just imports the library as:
import * as L from 'partial.lenses'
This library has historically been developed in a fairly aggressive manner so that features have been marked as obsolete and removed in subsequent major versions. This can be particularly burdensome for developers of libraries that depend on partial lenses. To help the development of such libraries, this section specifies a tiny subset of this library as stable. While it is possible that the stable subset is later extended, nothing in the stable subset will ever be changed in a backwards incompatible manner.
The following operations, with the below mentioned limitations, constitute the stable subset:
L.compose(...optics) ~> optic is stable with the exception
that one must not depend on being able to compose optics with ordinary
functions. Also, the use of arrays to denote composition is not part of the
stable subset. Note that L.compose() is guaranteed to be
equivalent to the L.identity optic.
L.get(lens, maybeData) ~> maybeValue is stable without
limitations.
L.lens(maybeData => maybeValue, (maybeValue, maybeData) => maybeData) ~> lens is stable with the exception that one must not depend on the
user specified getter and setter functions being passed more than 1 and 2
arguments, respectively, and one must make no assumptions about any extra
parameters being passed.
L.modify(optic, maybeValue => maybeValue, maybeData) ~> maybeData is stable with the exception that one must not depend
on the user specified function being passed more than 1 argument and one must
make no assumptions about any extra parameters being passed.
L.remove(optic, maybeData) ~> maybeData is stable without
limitations.
L.set(optic, maybeValue, maybeData) ~> maybeData is stable without
limitations.
The main intention behind the stable subset is to enable a dependent library to make basic use of lenses created by client code using the dependent library.
In retrospect, the stable subset has existed since version 2.2.0.
The main Partial Lenses library aims to provide robust general purpose combinators for dealing with plain JavaScript data. Combinators that are more experimental or specialized in purpose or would require additional dependencies aside from the Infestines library, which is mainly used for the currying helpers it provides, are not provided.
Currently the following additional Partial Lenses libraries exist:
The abstractions, traversals, lenses, and isomorphisms, provided by this library are collectively known as optics. Traversals can target any number of elements. Lenses are a restriction of traversals that target a single element. Isomorphisms are a restriction of lenses with an inverse.
In addition to basic bidirectional optics, this library also supports more arbitrary transforms using optics with sequencing and transform ops. Transforms allow operations, such as modifying a part of data structure multiple times or even in a loop, that are not possible with basic optics.
Some optics libraries provide many more abstractions, such as "optionals", "prisms" and "folds", to name a few, forming a DAG. Aside from being conceptually important, many of those abstractions are not only useful but required in a statically typed setting where data structures have precise constraints on their shapes, so to speak, and operations on data structures must respect those constraints at all times.
On the other hand, in a dynamically typed language like JavaScript, the shapes of run-time objects are naturally malleable. Nothing immediately breaks if a new object is created as a copy of another object by adding or removing a property, for example. We can exploit this to our advantage by considering all optics as partial and manage with a smaller amount of distinct classes of optics.
By definition, a total function, or just a function, is defined for all possible inputs. A partial function, on the other hand, may not be defined for all inputs.
As an example, consider an operation to return the first element of an array. Such an operation cannot be total unless the input is restricted to arrays that have at least one element. One might think that the operation could be made total by returning a special value in case the input array is empty, but that is no longer the same operation—the special value is not the first element of the array.
Now, in partial lenses, the idea is that in case the input does not match the
expectation of an optic, then the input is treated as being undefined, which
is the equivalent of non-existent: reading through the optic gives undefined
and writing through the optic replaces the focus with the written value. This
makes the optics in this library partial and allows specific partial optics,
such as the simple L.prop lens, to be used in a wider range of
situations than corresponding total optics.
Making all optics partial has a number of consequences. For one thing, it can
potentially hide bugs: an incorrectly specified optic treats the input as
undefined and may seem to work without raising an error. We have not found
this to be a major source of bugs in practice. However, partiality also has a
number of benefits. In particular, it allows optics to seamlessly support both
insertion and removal. It also allows to reduce the number of necessary
abstractions and it tends to make compositions of optics more concise with fewer
required parts, which both help to avoid bugs.
Optics in this library support a simple unnested form of indexing. When focusing on an array element or an object property, the index of the array element or the key of the object property is passed as the index to user defined functions operating on that focus.
For example:
L.get([L.find(R.equals('bar')), (value, index) => ({value, index})],
['foo', 'bar', 'baz'])
// {value: 'bar', index: 1}
L.modify(L.values, (value, key) => ({key, value}), {x: 1, y: 2})
// {x: {key: 'x', value: 1}, y: {key: 'y', value: 2}}
Only optics directly operating on array elements and object properties produce
indices. Most optics do not have an index of their own and they pass the index
given by the preceding optic as their focus. For example, L.when
doesn't have an index by itself, but it passes through the index provided by the
preceding optic:
L.collectAs((value, index) => ({value, index}),
[L.elems, L.when(x => x > 2)],
[3, 1, 4, 1])
// [{value: 3, index: 0}, {value: 4, index: 2}]
L.collectAs((value, key) => ({value, key}),
[L.values, L.when(x => x > 2)],
{x: 3, y: 1, z: 4, w: 1})
// [{value: 3, key: 'x'}, {value: 4, key: 'z'}]
When accessing a focus deep inside a data structure, the indices along the path
to the focus are not collected into a path. However, it is possible to define
combinators to construct paths. The reason for not collecting paths by default
is that doing so would be relatively expensive due to additional allocations.
The L.choose combinator can be useful in cases where there is a
need to access some index or context along the path to a focus.
Starting with version 10.0.0, to strongly guide away from
mutating data structures, optics call
Object.freeze
on any new objects they create when NODE_ENV is not production.
Why only non-production builds? Because Object.freeze can be quite
expensive and the main benefit is in catching potential bugs early during
development.
Also note that optics do not implicitly "deep freeze" data structures given to them or freeze data returned by user defined functions. Only objects newly created by optic functions themselves are frozen.
Starting with version 13.10.0, the possibility that
optics do not unnecessarily clone input data structures is explicitly
acknowledged. In case all elements of an array or object produced by an optic
operation would be the same, as determined by
Object.is,
then it is allowed, but not guaranteed, for the optic operation to return the
input as is.
A lot of libraries these days claim to be composable. Is any collection of functions composable? In the opinion of the author of this library, in order for something to be called "composable", a couple of conditions must be fulfilled:
Conversely, if there is no operation to perform composition or there are no useful simplifying laws on how compositions behave, then one should not call such a thing composable.
Now, optics are composable in several ways and in each of those ways there is an operation to perform the composition and laws on how such composed optics behave. Here is a table of the means of composition supported by this library:
| Operation(s) | Semantics | |
|---|---|---|
| Nesting | L.compose(...optics) or [...optics] | Monoid over unityped optics |
| Recursing | L.lazy(optic => optic) | Fixed point |
| Adapting | L.choices(optic, ...optics) | Semigroup over optics |
| Querying | L.choice(...optics) and L.chain(value => optic, optic) | MonadPlus over optics |
| Picking | L.pick({...prop:lens}) | Product of lenses |
| Branching | L.branch({...prop:traversal}) | Coproduct of traversals |
| Sequencing | L.seq(...transforms) | Monad over transforms |
The above table and, in particular, the semantics column is by no means complete. In particular, the documentation of this library does not generally spell out proofs of the semantics.
Aside from understanding laws on how forms of composition behave, it is useful to understand laws that are specific to operations on lenses and optics, in general. As described in the paper A clear picture of lens laws, many laws have been formulated for lenses and it can be useful to have lenses that do not necessarily obey some laws.
Here is a snippet that demonstrates that partial lenses can obey the laws of, so called, very well-behaved lenses:
function test(actual, expected) {
return R.equals(actual, expected) || {actual, expected}
}
const VeryWellBehavedLens = ({lens, data, elemA, elemB}) => ({
GetSet: test(L.set(lens, L.get(lens, data), data), data),
SetGet: test(L.get(lens, L.set(lens, elemA, data)), elemA),
SetSet: test(L.set(lens, elemB, L.set(lens, elemA, data)),
L.set(lens, elemB, data))
})
VeryWellBehavedLens({
elemA: 2,
elemB: 3,
data: {x: 1},
lens: 'x'
})
// { GetSet: true, SetGet: true, SetSet: true }
You might want to ▶ play with the laws in your browser.
Note, however, that partial lenses are not (total) lenses. undefined is
given special meaning and should not appear in the manipulated data.
For some reason there seems to be a persistent myth that partial lenses cannot obey lens laws. The issue a little more interesting than a simple yes or no. The short answer is that partial lenses can obey lens laws. However, for practical reasons there are many combinators in this library that, alone, do not obey lens laws. Nevertheless even such combinators can be used in lens compositions that obey lens laws.
Consider the L.find combinator. The truth is that it doesn't by
itself obey lens laws. Here is an example:
L.get(L.find(R.equals(1)),
L.set(L.find(R.equals(1)), 2, []))
// undefined
As you can see, L.find(R.equals(1)) does not obey the SetGet aka
Put-Get law. Does this make the L.find combinator useless? Far
from it.
Consider the following lens:
const valOf = key => [L.find(R.whereEq({key})), L.defaults({key}), 'val']
The valOf lens constructor is for accessing association arrays that contain
{key, val} pairs. For example:
const sampleAssoc = [{key: 'x', val: 42}, {key: 'y', val: 24}]
L.set(valOf('x'), 101, [])
// [{key: 'x', val: 101}]
L.get(valOf('x'), sampleAssoc)
// 42
L.get(valOf('z'), sampleAssoc)
// undefined
L.set(valOf('x'), undefined, sampleAssoc)
// [{key: 'y', val: 24}]
L.set(valOf('x'), 13, sampleAssoc)
// [{key: 'x', val: 13}, {key: 'y', val: 24}]
It obeys lens laws:
VeryWellBehavedLens({
elemA: 2,
elemB: 3,
data: [{key: 'x', val: 13}],
lens: valOf('x')
})
Before you try to break it, note that a lens returned by valOf(key) is only
supposed to work on valid association arrays. A valid association array must
not contain duplicate keys, undefined is not valid val, and the order of
elements is not significant. (Note that you could also add
L.rewrite(R.sortBy(L.get('key'))) to the composition to ensure
that elements stay in the same order.)
The gist of this example is important. Even if it is the case that not all
parts of a lens composition obey lens laws, it can be that a composition taken
as a whole obeys lens laws. The reason why this use of L.find
results in a lawful partial lens is that the lenses composed after it restricts
the scope of the lens so that one cannot modify the key.
L.assign(optic, object, maybeData) ~> maybeData v11.13.0L.assign allows one to merge the given object into the object or objects
focused on by the given optic.
For example:
L.assign(L.elems, {y: 1}, [{x: 3, y: 2}, {x: 4}])
// [ { x: 3, y: 1 }, { x: 4, y: 1 } ]
L.modify(optic, (maybeValue, index) => maybeValue, maybeData) ~> maybeData v2.2.0L.modify allows one to map over the elements focused on by the given optic.
For example:
L.modify(['elems', 0, 'x'], R.inc, {elems: [{x: 1, y: 2}, {x: 3, y: 4}]})
// { elems: [ { x: 2, y: 2 }, { x: 3, y: 4 } ] }
L.modify(['elems', L.elems, 'x'],
R.dec,
{elems: [{x: 1, y: 2}, {x: 3, y: 4}]})
// { elems: [ { x: 0, y: 2 }, { x: 2, y: 4 } ] }
L.remove(optic, maybeData) ~> maybeData v2.0.0L.remove allows one to remove the elements focused on by the given optic.
For example:
L.remove([0, L.defaults({}), 'x'], [{x: 1}, {x: 2}, {x: 3}])
// [ { x: 2 }, { x: 3 } ]
L.remove([L.elems, 'x', L.when(x => x > 1)], [{x: 1}, {x: 2, y: 1}, {x: 3}])
// [ { x: 1 }, { y: 1 }, {} ]
Note that L.remove(optic, maybeData) is equivalent to L.set(lens, undefined, maybeData). With partial lenses, setting to undefined typically has
the effect of removing the focused element.
L.set(optic, maybeValue, maybeData) ~> maybeData v1.0.0L.set allows one to replace the elements focused on by the given optic with
the specified value.
For example:
L.set(['a', 0, 'x'], 11, {id: 'z'})
// {a: [{x: 11}], id: 'z'}
L.set([L.elems, 'x', L.when(x => x > 1)], -1, [{x: 1}, {x: 2, y: 1}, {x: 3}])
// [ { x: 1 }, { x: -1, y: 1 }, { x: -1 } ]
Note that L.set(lens, maybeValue, maybeData) is equivalent to L.modify(lens, R.always(maybeValue), maybeData).
L.traverse(algebra, (maybeValue, index) => operation, optic, maybeData) ~> operation v10.0.0L.traverse maps each focus to an operation and returns an operation that runs
those operations in-order and collects the results. The
algebra
argument must be either a
Functor,
Applicative,
or
Monad
depending on the optic as specified in L.toFunction.
Here is a bit involved example that uses the State applicative and L.traverse
to replace elements in a data structure by the number of times those elements
have appeared at that point in the data structure:
const State = {
of: result => state => ({state, result}),
ap: (x2yS, xS) => state0 => {
const {state: state1, result: x2y} = x2yS(state0)
const {state, result: x} = xS(state1)
return {state, result: x2y(x)}
},
map: (x2y, xS) => State.ap(State.of(x2y), xS),
run: (s, xS) => xS(s).result
}
const count = x => x2n => {
const k = `${x}`
const n = (x2n[k] || 0) + 1
return {result: n, state: L.set(k, n, x2n)}
}
State.run({}, L.traverse(State, count, L.elems, [1, 2, 1, 1, 2, 3, 4, 3, 4, 5]))
// [1, 1, 2, 3, 2, 1, 1, 2, 2, 1]
The L.compose combinator allows one to build optics that deal
with nested data structures.
L.compose(...optics) ~> optic or [...optics] v1.0.0L.compose creates a nested composition of the given optics and ordinary
functions such that in L.compose(bigger, smaller) the smaller optic can only
see and manipulate the part of the whole as seen through the bigger optic.
The following equations characterize composition:
L.compose() = L.identity
L.compose(l) = l
L.modify(L.compose(o, ...os)) = R.compose(L.modify(o), ...os.map(L.modify))
L.get(L.compose(o, ...os)) = R.pipe(L.get(o), ...os.map(L.get))
Furthermore, in this library, an array of optics [...optics] is treated as a
composition L.compose(...optics). Using the array notation, the above
equations can be written as:
[] = L.identity
[l] = l
L.modify([o, ...os]) = R.compose(L.modify(o), ...os.map(L.modify))
L.get([o, ...os]) = R.pipe(L.get(o), ...os.map(L.get))
For example:
L.set(['a', 1], 'a', {a: ['b', 'c']})
// { a: [ 'b', 'a' ] }
L.get(['a', 1], {a: ['b', 'c']})
// 'c'
You can also directly compose optics with ordinary functions. The result of such a composition is a read-only optic.
For example:
L.get(['x', x => x + 1], {x: 1})
// 2
L.set(['x', x => x + 1], 3, {x: 1})
// { x: 1 }
Note that eligible ordinary functions must have a maximum arity of two: the
first argument will be the data and second will be the index. Both can, of
course, be undefined. Also starting from version
11.0.0 it is not guaranteed that such ordinary functions
would not be passed other arguments and therefore such functions should not
depend on the number of arguments being passed nor on any arguments beyond the
first two.
Note that R.compose is not the same as
L.compose.
L.flat(...optics) ~> optic v13.6.0L.flat is like L.compose except that L.flatten
is composed around and between the given optics. In other words, L.flat(o1, ..., oN) is equivalent to L.compose(L.flatten, o1, L.flatten, ..., L.flatten, oN, L.flatten).
The L.lazy combinator allows one to build optics that deal with
nested or recursive data structures of arbitrary depth. It also allows one to
build transforms with loops.
L.lazy(optic => optic) ~> optic v5.1.0L.lazy can be used to construct optics lazily. The function given to L.lazy
is passed a forwarding proxy to its return value and can also make forward
references to other optics and possibly construct a recursive optic.
Note that when using L.lazy to construct a recursive optic, it will only work
in a meaningful way when the recursive uses are either precomposed
or presequenced with some other optic in a way that neither causes
immediate nor unconditional recursion.
For example, here is a traversal that targets all the primitive elements in a data structure of nested arrays and objects:
const primitives = [
L.optional,
L.lazy(rec => L.cond([R.is(Array), [L.elems, rec]],
[R.is(Object), [L.values, rec]],
[ L.identity]))]
Note that the above creates a cyclic representation of the traversal.
Now, for example:
L.collect(primitives, [[[1], 2], {y: 3}, [{l: 4, r: [5]}, {x: 6}]])
// [ 1, 2, 3, 4, 5, 6 ]
L.modify(primitives, x => x+1, [[[1], 2], {y: 3}, [{l: 4, r: [5]}, {x: 6}]])
// [ [ [ 2 ], 3 ], { y: 4 }, [ { l: 5, r: [ 6 ] }, { x: 7 } ] ]
L.remove([primitives, L.when(x => 3 <= x && x <= 4)],
[[[1], 2], {y: 3}, [{l: 4, r: [5]}, {x: 6}]])
// [ [ [ 1 ], 2 ], {}, [ { r: [ 5 ] }, { x: 6 } ] ]
Adapting combinators allow one to build optics that adapt to their input.
L.choices(optic, ...optics) ~> optic v11.10.0L.choices returns a partial optic that acts like the first of the given optics
whose view is not undefined on the given data structure. When the views of
all of the given optics are undefined, the returned optic acts like the last
of the given optics. See also L.choice.
For example:
L.set([L.elems, L.choices('a', 'd')], 3, [{R: 1}, {a: 1}, {d: 2}])
// [ { R: 1, d: 3 }, { a: 3 }, { d: 3 } ]
L.choose((maybeValue, index) => optic) ~> optic v1.0.0L.choose creates an optic whose operation is determined by the given function
that maps the underlying view, which can be undefined, to an optic. In other
words, the L.choose combinator allows an optic to be constructed after
examining the data structure being manipulated. See also L.cond.
For example:
const majorAxis =
L.choose(({x, y} = {}) => Math.abs(x) < Math.abs(y) ? 'y' : 'x')
L.get(majorAxis, {x: -3, y: 1})
// -3
L.modify(majorAxis, R.negate, {x: -3, y: 1})
// { x: 3, y: 1 }
L.cond(...[(maybeValue, index) => testable, consequentOptic][, [alternativeOptic]]) ~> optic v13.1.0L.cond creates an optic whose operation is selected from the given optics and
predicates on the underlying view. See also L.condOf,
L.choose and L.ifElse.
L.cond( [ predicate, consequent ]
, ...
[ , [ alternative ] ] )
L.cond is not curried unlike most functions in this library. L.cond can be
given any number of [predicate, consequent] pairs. The predicates are
functions on the underlying view and are tested sequentially. The consequents
are optics and L.cond acts like the consequent corresponding to the first
predicate that returns true. The last argument to L.cond can be an
[alternative] singleton, where the alternative is an optic to be used in
case none of the predicates return true. If all predicates return false and
there is no alternative, L.cond acts like L.zero.
For example:
const minorAxis =
L.cond([({x, y} = {}) => Math.abs(y) < Math.abs(x), 'y'], ['x'])
L.get(minorAxis, {x: -3, y: 1})
// 1
L.modify(minorAxis, R.negate, {x: -3, y: 1})
// { x: -3, y: -1 }
Note that it is better to omit the predicate from the alternative
L.cond(..., [alternative])
than to use a catch all predicate like R.T
L.cond(..., [R.T, alternative])
because in the latter case L.cond cannot determine that a user defined
predicate will always be true and has to construct a more expensive optic.
Note that L.cond can be implemented using L.choose, but not
vice versa. L.choose not only allows the optic to be chosen
dynamically, but also allows the optic to be constructed dynamically and using
the data at the focus.
L.condOf(lens, ...[(maybeValue, index) => testable, consequentOptic][, [alternativeOptic]]) ~> optic v13.5.0L.condOf is like L.cond except the first argument to L.condOf
is a lens to get the parameters for the predicates from the underlying view.
For example:
L.get(
L.condOf(
'type',
[R.equals('title'), 'text'],
[R.equals('text'), 'body']
),
{type: 'text', body: 'Try writing this with `L.cond`.'}
)
// 'Try writing this with `L.cond`.'
L.ifElse((maybeValue, index) => testable, optic, optic) ~> optic v13.1.0L.ifElse creates an optic whose operation is selected based on the given
predicate from the two given optics. If the predicate is truthy on the value at
focus, the first of the given optics is used. Otherwise the second of the given
optics is used. See also L.cond.
For example:
L.modify(L.ifElse(Array.isArray, L.elems, L.values), R.inc, [1, 2, 3])
// [ 2, 3, 4 ]
L.modify(L.ifElse(Array.isArray, L.elems, L.values), R.inc, {x: 1, y: 2, z: 3})
// { x: 2, y: 3, z: 4 }
L.iftes((maybeValue, index) => testable, consequentOptic, ...[, alternativeOptic]) ~> optic v11.14.0WARNING: L.iftes has been obsoleted. Use L.ifElse or
L.cond instead. See CHANGELOG for
details.
L.iftes creates an optic whose operation is selected from the given optics and
predicates on the underlying view.
L.iftes( predicate, consequent
[ , ... ]
[ , alternative ] )
L.iftes is not curried unlike most functions in this library. L.iftes
requires at least two arguments and successive arguments form predicate -
consequent pairs. The predicates are functions on the underlying view and are
tested sequentially. The consequents are optics and L.iftes acts like the
consequent corresponding to the first predicate that returns true. If L.iftes
is given an odd number of arguments, the last argument is the alternative
taken in case none of the predicates returns true. If all predicates return
false and there is no alternative, L.iftes acts like L.zero.
For example:
const minorAxis =
L.iftes(({x, y} = {}) => Math.abs(y) < Math.abs(x), 'y', 'x')
L.get(minorAxis, {x: -3, y: 1})
// 1
L.modify(minorAxis, R.negate, {x: -3, y: 1})
// { x: -3, y: -1 }
Note that L.iftes can be implemented using L.choose.
L.orElse(backupOptic, primaryOptic) ~> optic v2.1.0L.orElse(backupOptic, primaryOptic) acts like primaryOptic when its view is
not undefined and otherwise like backupOptic.
Note that L.choice(...optics) is equivalent to
optics.reduceRight(L.orElse, L.zero) and L.choices(...optics)
is equivalent to optics.reduce(L.orElse).
Querying combinators allow one to use optics to query data structures. Querying is distinguished from adapting in that querying defaults to an empty or read-only zero.
L.chain((value, index) => optic, optic) ~> optic v3.1.0L.chain provides a monadic
chain
combinator for querying with optics. L.chain(toOptic, optic) is equivalent to
L.compose(optic, L.choose((maybeValue, index) =>
maybeValue === undefined
? L.zero
: toOptic(maybeValue, index)))
Note that with the R.always, L.chain,
L.choice and L.zero combinators, one can consider
optics as subsuming the maybe monad.
L.choice(...optics) ~> optic v2.1.0L.choice returns a partial optic that acts like the first of the given optics
whose view is not undefined on the given data structure. When the views of
all of the given optics are undefined, the returned optic acts like
L.zero, which is the identity element of L.choice. See also
L.choices.
For example:
L.modify([L.elems, L.choice('a', 'd')], R.inc, [{R: 1}, {a: 1}, {d: 2}])
// [ { R: 1 }, { a: 2 }, { d: 3 } ]
L.optional ~> optic v3.7.0L.optional is an optic over an optional element. When used as a traversal,
and the focus is undefined, the traversal is empty. When used as a lens, and
the focus is undefined, the lens will be read-only.
As an example, consider the difference between:
L.set([L.elems, 'x'], 3, [{x: 1}, {y: 2}])
// [ { x: 3 }, { y: 2, x: 3 } ]
and:
L.set([L.elems, 'x', L.optional], 3, [{x: 1}, {y: 2}])
// [ { x: 3 }, { y: 2 } ]
Note that L.optional is equivalent to L.when(x => x !== undefined).
L.unless((maybeValue, index) => testable) ~> optic v12.1.0L.unless allows one to selectively skip elements within a traversal or to
selectively turn a lens into a read-only lens whose view is undefined. See
also L.when.
For example:
L.modify([L.elems, L.unless(x => x < 0)], R.negate, [0, -1, 2, -3, 4])
// [ -0, -1, -2, -3, -4 ]
L.when((maybeValue, index) => testable) ~> optic v5.2.0L.when allows one to selectively skip elements within a traversal or to
selectively turn a lens into a read-only lens whose view is undefined. See
also L.unless.
For example:
L.modify([L.elems, L.when(x => x > 0)], R.negate, [0, -1, 2, -3, 4])
// [ 0, -1, -2, -3, -4 ]
Note that L.when(p) is equivalent to L.choose((x, i) => p(x, i) ? L.identity : L.zero).
L.zero ~> optic v6.0.0L.zero is the identity element of L.choice and
L.chain. As a traversal, L.zero is a traversal of no elements
and as a lens, i.e. when used with L.get, L.zero is a read-only
lens whose view is always undefined.
For example:
L.collect([L.elems,
L.cond([R.is(Array), L.elems],
[R.is(Object), 'x'],
[L.zero])],
[1, {x: 2}, [3, 4]])
// [ 2, 3, 4 ]
L.log(...labels) ~> optic v3.2.0L.log(...labels) is an identity optic that outputs
console.log
messages with the given labels (or format in
Node.js) when
data flows in either direction, get or set, through the lens.
For example:
L.set(['x', L.log('x')], '11', {x: 10})
// x get 10
// x set 11
// { x: '11' }
L.set(['x', L.log('%s x: %j')], '11', {x: 10})
// get x: 10
// set x: '11'
// { x: '11' }
L.Constant ~> Functor v13.7.0L.Constant is the Static
Land
compatible constant
Functor
definition used by Partial Lenses.
L.Identity ~> Monad v13.7.0L.Identity is the Static
Land
compatible identity
Monad
definition used by Partial Lenses.
L.toFunction(optic) ~> optic v7.0.0L.toFunction converts a given optic, which can be a string, an
integer, an array, or a function to a function. This
can be useful for implementing new combinators that cannot otherwise be
implemented using the combinators provided by this library. See also
L.traverse.
For isomorphisms and lenses, the returned function will have the signature
(Maybe s, Index, Functor c, (Maybe a, Index) -> c b) -> c t
for traversals the signature will be
(Maybe s, Index, Applicative c, (Maybe a, Index) -> c b) -> c t
and for transforms the signature will be
(Maybe s, Index, Monad c, (Maybe a, Index) -> c b) -> c t
Note that the above signatures are written using the "tupled" parameter notation
(...) -> ... to denote that the functions are not curried.
The
Functor,
Applicative,
and
Monad
arguments are expected to conform to their Static
Land
specifications.
Note that, in conjunction with partial optics, it may be advantageous to have
the algebras to allow for partiality. With traversals it is also possible, for
example, to simply post compose optics with L.optional to skip
undefined elements.
Note that if you simply wish to perform an operation that needs roughly the full
expressive power of the underlying lens encoding, you should use
L.traverse, because it is independent of the underlying
encoding, while L.toFunction essentially exposes the underlying encoding and
it is better to avoid depending on that.
Ordinary optics are passive and bidirectional in such a way that the same optic can be both read and written through. The underlying implementation of this library also allows one to implement active operations that don't quite provide the same kind of passive bidirectionality, but can be used to flexibly modify data structures. Such operations are called transforms in this library.
Unlike ordinary optics, transforms allow for monadic sequencing, which makes it possible to operate on a part of data structure multiple times. This allows operations that are impossible to implement using ordinary optics, but also potentially makes it more difficult to reason about the results. This ability also makes it impossible to read through transforms in the same sense as with ordinary optics.
Recall that lenses have a single focus and traversals
have multiple focuses that can then be operated upon using various operations
such as L.modify. Although it is not strictly enforced by this
library, it is perhaps clearest to think that transforms have no focuses. A
transform using transform ops, that act as traversals of no
elements, can, and perhaps preferably should, be empty and should
be executed using L.transform, which, unlike
L.modify, takes no user defined operation to apply to focuses.
The line between transforms and optics is not entirely clear cut in the sense that it is technically possible to use various transform ops within an ordinary optic definition. Furthermore, it is also possible to use sequencing to create transforms that have focuses that can then be operated upon. The results of such uses don't quite follow the laws of ordinary optics, but may sometimes be useful.
L.transform(optic, maybeData) ~> maybeData v11.7.0L.transform(o, s) is shorthand for L.modify(o, x => x, s) and
is intended for running transforms defined using transform
ops.
Note that
L.assign(o, x, s) is equivalent to L.transform([o, L.assignOp(x)], s),L.modify(o, f, s) is equivalent to L.transform([o, L.modifyOp(f)], s),L.set(o, x, s) is equivalent to L.transform([o, L.setOp(x)], s), andL.remove(o, s) is equivalent to L.transform([o, L.removeOp], s).The L.seq combinator allows one to build transforms
that modify their focus more than once.
L.seq(...transforms) ~> transform v9.4.0L.seq creates a transform that modifies the focus with each of the given
transforms in sequence.
Here is an example of a bottom-up transform over a data structure of nested objects and arrays:
const everywhere = [
L.optional,
L.lazy(rec => L.cond([R.is(Array), L.seq([L.elems, rec], L.identity)],
[R.is(Object), L.seq([L.values, rec], L.identity)],
[ L.identity]))]
The above everywhere transform is similar to the
F.everywhere transform
of the fastener zipper-library. Note
that the above everywhere and the primitives example differ in
that primitives only targets the non-object and non-array elements of the data
structure while everywhere also targets those.
L.modify(everywhere, x => [x], {xs: [{x: 1}, {x: 2}]})
// [ { xs: [ [ [ { x: [ 1 ] } ], [ { x: [ 2 ] } ] ] ] } ]
Note that L.seq, L.choose, and L.setOp can be
combined together as a
Monad
chain(x2t, t) = L.seq(t, L.choose(x2t))
of(x) = L.setOp(x)
which is not the same as the querying monad.
L.assignOp(object) ~> optic v11.13.0L.assignOp creates an optic that merges the given object into the object in
focus.
For example:
L.transform([L.elems, L.assignOp({y: 1})], [{x: 3}, {x: 4, y: 5}])
// [ { x: 3, y: 1 }, { x: 4, y: 1 } ]
L.modifyOp((maybeValue, index) => maybeValue) ~> optic v11.7.0L.modifyOp creates an optic that maps the focus with the given function. When
used as a traversal, L.modifyOp acts as a traversal of no elements. When used
as a lens, L.modifyOp acts as a read-only lens whose view is the mapped focus.
Usually, however, L.modifyOp is used within transforms.
For example:
L.transform(L.branch({xs: [L.elems, L.modifyOp(R.inc)],
z: [L.optional, L.modifyOp(R.negate)],
ys: [L.elems, L.modifyOp(R.dec)]}),
{xs: [1, 2, 3],
ys: [1, 2, 3]})
// { xs: [ 2, 3, 4 ],
// ys: [ 0, 1, 2 ] }
L.removeOp ~> optic v11.7.0L.removeOp is shorthand for L.setOp(undefined).
Here is an example based on a question from a user:
const sampleToFilter = {elements: [{time: 1, subelements: [1, 2, 3, 4]},
{time: 2, subelements: [1, 2, 3, 4]},
{time: 3, subelements: [1, 2, 3, 4]}]}
L.transform(['elements',
L.elems,
L.ifElse(elem => elem.time < 2, L.removeOp,
['subelements', L.elems, L.when(i => i < 3), L.removeOp])],
sampleToFilter)
// { elements: [ { time: 2, subelements: [ 3, 4 ] },
// { time: 3, subelements: [ 3, 4 ] } ] }
The idea is to filter the data both by time and by subelements.
L.setOp(maybeValue) ~> optic v11.7.0L.setOp(x) is shorthand for L.modifyOp(R.always(x)).
A traversal operates over a collection of non-overlapping focuses that are visited only once and can, for example, be collected, folded, modified, set and removed. Put in another way, a traversal specifies a set of paths to elements in a data structure.
L.branch({prop: traversal, ...props}) ~> traversal v5.1.0L.branch creates a new traversal from a given possibly nested template object
that specifies how the new traversal should visit the properties of an object.
If one thinks of traversals as specifying sets of paths, then the template can
be seen as mapping each property to a set of paths to traverse.
For example:
L.collect(L.branch({first: L.elems, second: {value: L.identity}}),
{first: ['x'], second: {value: 'y'}})
// [ 'x', 'y' ]
The use of L.identity above might be puzzling at first.
L.identity essentially specifies an empty path. So, when a
property is mapped to L.identity in the template given to
L.branch, it means that the element is to be visited by the resulting
traversal.
Note that L.branch is equivalent to L.branchOr(L.zero).
Note that you can also compose L.branch with other optics. For example, you
can compose with L.pick to create a traversal over specific
elements of an array:
L.modify([L.pick({z: 2, x: 0}),
L.branch({x: L.identity, z: L.identity})],
R.negate,
[1, 2, 3])
// [ -1, 2, -3 ]
See the BST traversal section for a more meaningful example.
L.branchOr(traversal, {prop: traversal, ...props}) ~> traversal v13.2.0L.branchOr creates a new traversal from a given traversal and a given possibly
nested template object. The template specifies how the new traversal should
visit the corresponding properties of an object. The separate traversal is used
for properties not defined in the template.
For example:
L.transform(L.branchOr(L.modifyOp(R.inc), {x: L.modifyOp(R.dec)}), {x: 0, y: 0})
// { x: -1, y: 1 }
Note that L.branch is equivalent to L.branchOr(L.zero) and
L.values is equivalent to L.branchOr(L.identity, {}).
L.branches(...propNames) ~> traversal v13.5.0L.branches creates a new traversal that visits the specified properties of an
object. L.branches(p1, ..., pN) is equivalent to L.branch({[p1]: [], ..., [pN]: []}).
L.children ~> traversal v13.3.0L.children is a traversal over the immediate children of the ordinary array or
plain object in focus. Children of objects whose constructor is neither Array
nor Object are not traversed. See also L.leafs.
For example:
L.modify(L.children, R.negate, {x: 3, y: 1})
// {x: -3, y: -1}
L.modify(L.children, R.negate, [1, 2, 3])
// [-1, -2, -3]
L.elems ~> traversal v7.3.0L.elems is a traversal over the elements of an array-like
object. When written through, L.elems always produces an Array. See also
L.values and L.elemsTotal.
For example:
L.modify(['xs', L.elems, 'x'], R.inc, {xs: [{x: 1}, {x: 2}]})
// { xs: [ { x: 2 }, { x: 3 } ] }
Just like with other optics operating on array-like objects, when
manipulating non-Array objects, L.rewrite can be used to
convert the result to the desired type, if necessary:
L.modify([L.rewrite(xs => Int8Array.from(xs)), L.elems],
R.inc,
Int8Array.from([-1, 4, 0, 2, 4]))
// Int8Array [ 0, 5, 1, 3, 5 ]
L.elemsTotal ~> traversal v13.11.0L.elemsTotal is a traversal over the elements of an array-like
object. When written through, L.elemsTotal always produces an Array.
Unlike L.elems, L.elemsTotal does not remove undefined
elements from the resulting array when written through.
For example:
L.modify([L.elemsTotal, L.when(R.is(Number))], R.negate, [1, undefined, 2])
// [-1, undefined, -2]
L.entries ~> traversal v11.21.0L.entries is a traversal over the entries, or [key, value] pairs, of an
object.
For example:
L.modify(L.entries, ([k, v]) => [v, k], {x: 'a', y: 'b'})
// { a: 'x', b: 'y' }
L.flatten ~> traversal v11.16.0L.flatten is a traversal over the elements of arbitrarily nested arrays.
Other array-like objects are treated as elements by L.flatten.
In case the immediate target of L.flatten is neither undefined nor an array,
it is traversed.
For example:
L.join(' ', L.flatten, [[[1]], ['2'], 3])
// '1 2 3'
L.keys ~> traversal v11.21.0L.keys is a traversal over the keys of an object.
For example:
L.modify(L.keys, R.toUpper, {x: 1, y: 2})
// { X: 1, Y: 2 }
L.leafs ~> traversal v13.3.0L.leafs is a traversal that descends into ordinary arrays and plain objects
and focuses on non-undefined elements whose constructor is neither Array nor
Object. See also L.children.
For example:
L.modify(L.leafs, R.negate, [{x: 1, y: [2]}, 3])
// [{x: -1, y: [-2]}, -3]
L.matches(/.../g) ~> traversal v10.4.0L.matches, when given a regular expression with the
global
flag, /.../g, is a partial traversal over the matches that the regular
expression gives over the focused string. See also L.matches.
For example:
L.collect([L.matches(/[^&=?]+=[^&=]+/g),
L.pick({name: L.matches(/^[^=]+/),
value: L.matches(/[^=]+$/)})],
'?first=foo&second=bar')
// [ { name: 'first', value: 'foo' },
// { name: 'second', value: 'bar' } ]
Note that an empty match terminates the traversal. It is possible to make use of that feature, but it is also possible that an empty match is due to an incorrect regular expression that can match the empty string.
L.query(...traversals) ~> traversal v13.6.0L.query is a traversal that searches for
defined elements within a nested data structure of ordinary
arrays and plain objects that are focused on by the given sequence of
traversals. L.query gives similar power as the descendant
combinator
of CSS selectors.
Recall the tutorial example. Perhaps the easiest way to focus on all the texts is to just query for them:
L.collect(L.query('text'), sampleTitles)
// [ 'Title', 'Rubrik' ]
So, to convert all the texts to upper case, one could write:
L.modify(L.query('text'), R.toUpper, sampleTitles)
// { titles: [
// { language: 'en', text: 'TITLE' },
// { language: 'sv', text: 'RUBRIK' } ] }
To only modify the text of a specific language, one could write:
L.modify(
L.query(L.when(R.propEq('language', 'en')), 'text'),
R.toUpper,
sampleTitles
)
// { titles: [
// { language: 'en', text: 'TITLE' },
// { language: 'sv', text: 'Rubrik' } ] }
And one can also view the text of a specific language using select:
L.select(L.query(L.when(R.propEq('language', 'sv')), 'text'), sampleTitles)
// 'Rubrik'
Like CSS selectors, L.query can be quite convenient, but should be used with
care. The search for matching elements can be expensive and specifying a query
that matches precisely the desired elements can be difficult.
Note that L.query(...ts), in general, is equivalent to ts.map(t => [L.satisfying(L.isDefined(t)), t]) and
L.query(L.when(predicate)) is equivalent to
L.satisfying(predicate).
L.satisfying((maybeValue, index) => testable) ~> traversal v13.3.0L.satisfying is a traversal that focuses on elements that satisfy the given
predicate within a nested data structure of ordinary arrays and plain objects.
Children of objects whose constructor is neither Array nor Object are not
traversed. See also L.query.
L.values ~> traversal v7.3.0L.values is a traversal over the values of an instanceof Object. When
written through, L.values always produces an Object. See also
L.elems.
For example:
L.modify(L.values, R.negate, {a: 1, b: 2, c: 3})
// { a: -1, b: -2, c: -3 }
When manipulating objects with a non-Object constructor
function XYZ(x, y, z) {
this.x = x
this.y = y
this.z = z
}
XYZ.prototype.norm = function () {
return (this.x * this.x +
this.y * this.y +
this.z * this.z)
}
L.rewrite can be used to convert the result to the desired type,
if necessary:
const objectTo = C => o => Object.assign(Object.create(C.prototype), o)
L.modify([L.rewrite(objectTo(XYZ)), L.values],
R.negate,
new XYZ(1, 2, 3))
// XYZ { x: -1, y: -2, z: -3 }
Note that L.values is equivalent to L.branchOr(L.identity, {}).
L.all((maybeValue, index) => testable, traversal, maybeData) ~> boolean v9.6.0L.all determines whether all of the elements focused on by the given traversal
satisfy the given predicate.
For example:
L.all(x => 1 <= x && x <= 6,
primitives,
[[[1], 2], {y: 3}, [{l: 4, r: [5]}, {x: 6}]])
// true
See also: L.any, L.none, and
L.selectAs.
L.and(traversal, maybeData) ~> boolean v9.6.0L.and determines whether all of the elements focused on by the given traversal
are truthy.
For example:
L.and(L.elems, [])
// true
Note that L.and is equivalent to L.all(x => x). See also:
L.or.
L.any((maybeValue, index) => testable, traversal, maybeData) ~> boolean v9.6.0L.any determines whether any of the elements focused on by the given traversal
satisfy the given predicate.
For example:
L.any(x => x > 5,
primitives,
[[[1], 2], {y: 3}, [{l: 4, r: [5]}, {x: 6}]])
// true
See also: L.all, L.none, and
L.selectAs.
L.collect(traversal, maybeData) ~> [...values] v3.6.0L.collect returns an array of the non-undefined elements focused on by the
given traversal or lens from a data structure.
For example:
L.collect(['xs', L.elems, 'x'], {xs: [{x: 1}, {x: 2}]})
// [ 1, 2 ]
Note that L.collect is equivalent to L.collectAs(x => x).
L.collectAs((maybeValue, index) => maybeValue, traversal, maybeData) ~> [...values] v7.2.0L.collectAs returns an array of the elements focused on by the given traversal
or lens from a data structure and mapped by the given function to a
non-undefined value.
For example:
L.collectAs(R.negate, ['xs', L.elems, 'x'], {xs: [{x: 1}, {x: 2}]})
// [ -1, -2 ]
L.collectAs(toMaybe, traversal, maybeData) is equivalent to
L.concatAs(toCollect, Collect, [traversal, toMaybe], maybeData)
where Collect and toCollect are defined as follows:
const Collect = {empty: R.always([]), concat: R.concat}
const toCollect = x => x !== undefined ? [x] : []
So:
L.concatAs(toCollect,
Collect,
['xs', L.elems, 'x', R.negate],
{xs: [{x: 1}, {x: 2}]})
// [ -1, -2 ]
The internal implementation of L.collectAs is optimized and faster than the
above naïve implementation.
L.concat(monoid, traversal, maybeData) ~> value v7.2.0L.concat({empty, concat}, t, s) performs a fold, using the given concat and
empty operations, over the elements focused on by the given traversal or lens
t from the given data structure s. The concat operation and the constant
returned by empty() should form a
monoid
over the values focused on by t.
For example:
const Sum = {empty: () => 0, concat: (x, y) => x + y}
L.concat(Sum, L.elems, [1, 2, 3])
// 6
Note that L.concat is staged so that after given the first argument,
L.concat(m), a computation step is performed.
L.concatAs((maybeValue, index) => value, monoid, traversal, maybeData) ~> value v7.2.0L.concatAs(xMi2r, {empty, concat}, t, s) performs a map, using given function
xMi2r, and fold, using the given concat and empty operations, over the
elements focused on by the given traversal or lens t from the given data
structure s. The concat operation and the constant returned by empty()
should form a
monoid
over the values returned by xMi2r.
For example:
L.concatAs(x => x, Sum, L.elems, [1, 2, 3])
// 6
Note that L.concatAs is staged so that after given the first two arguments,
L.concatAs(f, m), a computation step is performed.
L.count(traversal, maybeData) ~> number v9.7.0L.count goes through all the elements focused on by the traversal and counts
the number of non-undefined elements.
For example:
L.count([L.elems, 'x'], [{x: 11}, {y: 12}])
// 1
L.countIf((maybeValue, index) => testable, traversal, maybeData) ~> number v11.2.0L.countIf goes through all the elements focused on by the traversal and counts
the number of elements for which the given predicate returns a truthy value.
For example:
L.countIf(L.isDefined('x'), L.elems, [{x: 11}, {y: 12}])
// 1
L.counts(traversal, maybeData) ~> map v11.21.0L.counts returns a
map
of the counts of distinct values, including undefined, focused on by the given
traversal.
For example:
Array.from(L.counts(L.elems, [3, 1, 4, 1]).entries())
// [[3, 1], [1, 2], [4, 1]]
L.countsAs((maybeValue, index) => any, traversal, maybeData) ~> map v11.21.0L.countsAs returns a
map
of the counts of distinct values, including undefined, returned by the given
function from the values focused on by the given traversal.
For example:
Array.from(L.countsAs(Math.abs, L.elems, [3, -1, 4, 1]).entries())
// [[3, 1], [1, 2], [4, 1]]
L.foldl((value, maybeValue, index) => value, value, traversal, maybeData) ~> value v7.2.0L.foldl performs a fold from left over the elements focused on by the given
traversal. This is much like the
reduce
method of JavaScript arrays.
For example:
L.foldl((x, y) => x + y, 0, L.elems, [1, 2, 3])
// 6
Note that L.forEachWith is much like an imperative version
of L.foldl. Consider using it instead of using L.foldl with an imperative
accumulator procedure.
L.foldr((value, maybeValue, index) => value, value, traversal, maybeData) ~> value v7.2.0L.foldr performs a fold from right over the elements focused on by the given
traversal. This is much like the
reduceRight
method of JavaScript arrays.
For example:
L.foldr((x, y) => x * y, 1, L.elems, [1, 2, 3])
// 6
L.forEach((maybeValue, index) => undefined, traversal, maybeData) ~> undefined v11.20.0L.forEach calls the given function for each focus of the traversal.
For example:
L.forEach(console.log, [L.elems, 'x', L.elems], [{x: [3]}, {x: [1, 4]}, {x: [1]}])
// 3 0
// 1 0
// 4 1
// 1 0
L.forEachWith(() => context, (context, maybeValue, index) => undefined, traversal, maybeData) ~> context v13.4.0L.forEachWith first calls the given thunk to get or create a context. Then it
calls the given function, with context as the first argument, for each focus of
the traversal. Finally the context is returned. This is much like an
imperative version of L.foldl.
For example:
L.forEachWith(() => new Map(), (m, v, k) => m.set(k, v), L.values, {x: 2, y: 1})
// Map { 'x' => 2, 'y' => 1 }
Note that a new Map is returned each time the above expression is evaluated.
L.isDefined(traversal, maybeData) ~> boolean v11.8.0L.isDefined determines whether or not the given traversal focuses on any
non-undefined element on the given data structure. When used with a lens,
L.isDefined basically allows you to check whether the target of the lens
exists or, in other words, whether the data structure has the targeted element.
See also L.isEmpty.
For example:
L.isDefined('x', {y: 1})
// false
L.isEmpty(traversal, maybeData) ~> boolean v11.5.0L.isEmpty determines whether or not the given traversal focuses on any
elements, undefined or otherwise, on the given data structure. Note that when
used with a lens, L.isEmpty always returns false, because lenses always have
a single focus. See also L.isDefined.
For example:
L.isEmpty(L.flatten, [[], [[[], []], []]])
// true
L.join(string, traversal, maybeData) ~> string v11.2.0L.join creates a string by joining the optional elements targeted by the given
traversal with the given delimiter.
For example:
L.join(', ', [L.elems, 'x'], [{x: 1}, {y: 2}, {x: 3}])
// '1, 3'
L.joinAs((maybeValue, index) => maybeString, string, traversal, maybeData) ~> string v11.2.0L.joinAs creates a string by converting the elements targeted by the given
traversal to optional strings with the given function and then joining those
strings with the given delimiter.
For example:
L.joinAs(JSON.stringify, ', ', L.elems, [{x: 1}, {y: 2}])
// '{'x':1}, {'y':2}'
L.maximum(traversal, maybeData) ~> maybeValue v7.2.0L.maximum computes a maximum of the optional elements targeted by the
traversal.
For example:
L.maximum(L.elems, [1, 2, 3])
// 3
Note that elements are ordered according to the > operator.
L.maximumBy((maybeValue, index) => maybeKey, traversal, maybeData) ~> maybeValue v11.2.0L.maximumBy computes a maximum of the elements targeted by the traversal based
on the optional keys returned by the given function. Elements for which the
returned key is undefined are skipped.
For example:
L.maximumBy(R.length, L.elems, ['first', 'second', '--||--', 'third'])
// 'second'
Note that keys are ordered according to the > operator.
L.mean(traversal, maybeData) ~> number v11.17.0L.mean computes the arithmetic mean of the optional numbers targeted by the
traversal.
For example:
L.mean([L.elems, 'x'], [{x: 1}, {ignored: 3}, {x: 2}])
// 1.5
L.meanAs((maybeValue, index) => maybeNumber, traversal, maybeData) ~> number v11.17.0L.meanAs computes the arithmetic mean of the optional numbers returned by the
given function for the elements targeted by the traversal.
For example:
L.meanAs((x, i) => x <= i ? undefined : x, L.elems, [3, 1, 4, 1])
// 3.5
L.minimum(traversal, maybeData) ~> maybeValue v7.2.0L.minimum computes a minimum of the optional elements targeted by the
traversal.
For example:
L.minimum(L.elems, [1, 2, 3])
// 1
Note that elements are ordered according to the < operator.
L.minimumBy((maybeValue, index) => maybeKey, traversal, maybeData) ~> maybeValue v11.2.0L.minimumBy computes a minimum of the elements targeted by the traversal based
on the optional keys returned by the given function. Elements for which the
returned key is undefined are skipped.
For example:
L.minimumBy(L.get('x'), L.elems, [{x: 1}, {x: -3}, {x: 2}])
// {x: -3}
Note that keys are ordered according to the < operator.
L.none((maybeValue, index) => testable, traversal, maybeData) ~> boolean v11.6.0L.none determines whether none of the elements focused on by the given
traversal satisfy the given predicate.
For example:
L.none(x => x > 5,
primitives,
[[[1], 2], {y: 3}, [{l: 4, r: [5]}, {x: 6}]])
// false
See also: L.all, L.any, and L.selectAs.
L.or(traversal, maybeData) ~> boolean v9.6.0L.or determines whether any of the elements focused on by the given traversal
is truthy.
For example:
L.or(L.elems, [])
// false
Note that L.or is equivalent to L.any(x => x). See also:
L.and.
L.product(traversal, maybeData) ~> number v7.2.0L.product computes the product of the optional numbers targeted by the
traversal.
For example:
L.product(L.elems, [1, 2, 3])
// 6
L.productAs((maybeValue, index) => number, traversal, maybeData) ~> number v11.2.0L.productAs computes the product of the numbers returned by the given function
for the elements targeted by the traversal.
For example:
L.productAs((x, i) => x + i, L.elems, [3, 2, 1])
// 27
Note that unlike many other folds, L.productAs expects the function to only
return numbers and undefined is not treated in a special way. If you need to
skip elements, you can return the number 1.
L.select(traversal, maybeData) ~> maybeValue v9.8.0L.select goes lazily over the elements focused on by the given traversal and
returns the first non-undefined element.
L.select([L.elems, 'y'], [{x:1}, {y:2}, {z:3}])
// 2
Note that L.select is equivalent to L.selectAs(x => x).
L.selectAs((maybeValue, index) => maybeValue, traversal, maybeData) ~> maybeValue v9.8.0L.selectAs goes lazily over the elements focused on by the given traversal,
applying the given function to each element, and returns the first
non-undefined value returned by the function.
L.selectAs(x => x > 3 ? -x : undefined, L.elems, [3, 1, 4, 1, 5])
// -4
L.selectAs operates lazily. The user specified function is only applied to
elements until the first non-undefined value is returned and after that
L.selectAs returns without examining more elements.
Note that L.selectAs can be used to implement many other operations over
traversals such as finding an element matching a predicate and checking whether
all/any elements match a predicate. For example, here is how you could
implement a for all predicate over traversals:
const all = (p, t, s) => !L.selectAs(x => p(x) ? undefined : true, t, s)
Now:
all(x => x < 9,
primitives,
[[[1], 2], {y: 3}, [{l: 4, r: [5]}, {x: 6}]])
// true
L.sum(traversal, maybeData) ~> number v7.2.0L.sum computes the sum of the optional numbers targeted by the traversal.
For example:
L.sum(L.elems, [1, 2, 3])
// 6
L.sumAs((maybeValue, index) => number, traversal, maybeData) ~> number v11.2.0L.sumAs computes the sum of the numbers returned by the given function for the
elements targeted by the traversal.
For example:
L.sumAs((x, i) => x + i, L.elems, [3, 2, 1])
// 9
Note that unlike many other folds, L.sumAs expects the function to only return
numbers and undefined is not treated in a special way. If you need to skip
elements, you can return the number 0.
Lenses always have a single focus which can be viewed directly. Put in another way, a lens specifies a path to a single element in a data structure.
L.get(lens, maybeData) ~> maybeValue v2.2.0L.get returns the element focused on by a lens from a data
structure.
For example:
L.get('y', {x: 112, y: 101})
// 101
Note that L.get does not work on traversals.
L.lens((maybeData, index) => maybeValue, (maybeValue, maybeData, index) => maybeData) ~> lens v1.0.0L.lens creates a new primitive lens. The first parameter is the getter and
the second parameter is the setter. The setter takes two parameters: the
first is the value written and the second is the data structure to write into.
One should think twice before introducing a new primitive lens—most of the
combinators in this library have been introduced to reduce the need to write new
primitive lenses. With that said, there are still valid reasons to create new
primitive lenses. For example, here is a lens that we've used in production,
written with the help of Moment.js, to bidirectionally
convert a pair of start and end times to a duration:
const timesAsDuration = L.lens(
({start, end} = {}) => {
if (undefined === start)
return undefined
if (undefined === end)
return 'Infinity'
return moment.duration(moment(end).diff(moment(start))).toJSON()
},
(duration, {start = moment().toJSON()} = {}) => {
if (undefined === duration || 'Infinity' === duration) {
return {start}
} else {
return {
start,
end: moment(start).add(moment.duration(duration)).toJSON()
}
}
}
)
Now, for example:
L.get(timesAsDuration,
{start: '2016-12-07T09:39:02.451Z',
end: moment('2016-12-07T09:39:02.451Z').add(10, 'hours').toISOString()})
// 'PT10H'
L.set(timesAsDuration,
'PT10H',
{start: '2016-12-07T09:39:02.451Z',
end: '2016-12-07T09:39:02.451Z'})
// { end: '2016-12-07T19:39:02.451Z',
// start: '2016-12-07T09:39:02.451Z' }
When composed with L.pick, to flexibly pick the start and end
times, the above can be adapted to work in a wide variety of cases. However,
the above lens will never be added to this library, because it would require
adding dependency to Moment.js.
See the Interfacing with Immutable.js section for another
example of using L.lens.
L.setter((maybeValue, maybeData, index) => maybeData) ~> lens v10.3.0L.setter(set) is shorthand for L.lens(x => x, set).
L.foldTraversalLens((traversal, maybeData) => maybeValue, traversal) ~> lens v11.5.0L.foldTraversalLens creates a lens from a fold and a traversal. To make
sense, the fold should compute or pick a representative from the elements
focused on by the traversal such that when all the elements are equal then so is
the representative.
For example:
L.get(L.foldTraversalLens(L.minimum, L.elems), [3, 1, 4])
// 1
L.set(L.foldTraversalLens(L.minimum, L.elems), 2, [3, 1, 4])
// [ 2, 2, 2 ]
See the Collection toggle section for a more interesting example.
L.defaults(valueIn) ~> lens v2.0.0L.defaults is used to specify a default context or value for an element in
case it is missing. When set with the default value, the effect is to remove
the element. This can be useful for both making partial lenses with propagating
removal and for avoiding having to check for and provide default values
elsewhere.
For example:
L.get(['items', L.defaults([])], {})
// []
L.get(['items', L.defaults([])], {items: [1, 2, 3]})
// [ 1, 2, 3 ]
L.set(['items', L.defaults([])], [], {items: [1, 2, 3]})
// {}
Note that L.defaults(valueIn) is equivalent to L.replace(undefined, valueIn).
L.define(value) ~> lens v1.0.0L.define is used to specify a value to act as both the default value and the
required value for an element.
L.get(['x', L.define(null)], {y: 10})
// null
L.set(['x', L.define(null)], undefined, {y: 10})
// { y: 10, x: null }
Note that L.define(value) is equivalent to [L.required(value), L.defaults(value)].
L.normalize((value, index) => maybeValue) ~> lens v1.0.0L.normalize maps the value with same given transform when read and written and
implicitly maps undefined to undefined. L.normalize(fn) is equivalent to
composing L.reread(fn) and L.rewrite(fn).
One use case for normalize is to make it easy to determine whether, after a
change, the data has actually changed. By keeping the data normalized, a simple
R.equals comparison will do.
L.required(valueOut) ~> lens v1.0.0L.required is used to specify that an element is not to be removed; in case it
is removed, the given value will be substituted instead.
For example:
L.remove(['item'], {item: 1})
// {}
L.remove(['item', L.required(null)], {item: 1})
// { item: null }
Note that L.required(valueOut) is equivalent to L.replace(valueOut, undefined).
L.reread((valueIn, index) => maybeValueIn) ~> lens v11.21.0L.reread maps the value with the given transform on read and implicitly maps
undefined to undefined. See also L.normalize.
L.rewrite((valueOut, index) => maybeValueOut) ~> lens v5.1.0L.rewrite maps the value with the given transform when written and implicitly
maps undefined to undefined. See also L.normalize.
One use case for rewrite is to re-establish data structure invariants after
changes.
See the BST as a lens section for a meaningful example.
Objects that have a non-negative integer length and strings, which are not
considered Object instances in JavaScript, are considered array-like objects
by partial optics. See also L.seemsArrayLike.
When writing through a lens or traversal that operates on array-like objects,
the result is always a plain Array. For example:
L.set(1, 'a', 'LoLa')
// [ 'L', 'a', 'L', 'a' ]
It may seem like the result should be of the same type as the object being manipulated, but that is problematic, because
Therefore, instead, when manipulating strings or array-like non-Array objects,
L.rewrite can be used to explicitly convert the result to the
desired type, if necessary. For example:
L.set([L.rewrite(R.join('')), 1], 'a', 'LoLa')
// 'LaLa'
Also, when manipulating array-like objects, partial lenses generally ignore
everything but the length property and the integer properties from 0 to
length-1.
L.append ~> lens v1.0.0L.append is a write-only lens that can be used to append values to an
array-like object. The view of L.append is always undefined.
For example:
L.get(L.append, ['x'])
// undefined
L.set(L.append, 'x', undefined)
// [ 'x' ]
L.set(L.append, 'x', ['z', 'y'])
// [ 'z', 'y', 'x' ]
Note that L.append is equivalent to L.index(i) with the index
i set to the length of the focused array or 0 in case the focus is not a
defined array.
L.filter((maybeValue, index) => testable) ~> lens v1.0.0L.filter operates on array-like objects. When not viewing an
array-like object, the result is undefined. When viewing an array-like
object, only elements matching the given predicate will be returned. When set,
the resulting array will be formed by concatenating the elements of the set
array-like object and the elements of the complement of the filtered focus.
For example:
L.set(L.filter(x => x <= '2'), 'abcd', '3141592')
// [ 'a', 'b', 'c', 'd', '3', '4', '5', '9' ]
NOTE: If you are merely modifying a data structure, and don't need to limit
yourself to lenses, consider using the L.elems traversal composed
with L.when.
An alternative design for filter could implement a smarter algorithm to combine
arrays when set. For example, an algorithm based on edit
distance could be used to maintain
relative order of elements. While this would not be difficult to implement, it
doesn't seem to make sense, because in most cases use of
L.normalize or L.rewrite would be preferable.
Also, the L.elems traversal composed with L.when will
retain order of elements.
L.find((maybeValue, index, {hint: index}) => testable[, {hint: index}]) ~> lens v1.0.0L.find operates on array-like objects like
L.index, but the index to be viewed is determined by finding the
first element from the focus that matches the given predicate. When no matching
element is found the effect is same as with L.append.
L.remove(L.find(x => x <= 2), [3, 1, 4, 1, 5, 9, 2])
// [ 3, 4, 1, 5, 9, 2 ]
L.find is designed to operate efficiently when used repeatedly. To this end,
L.find can be given an object with a hint property and when no hint object
is passed, a new object will be allocated internally. Repeated searches are
started from the closest existing index to the hint and then by increasing
distance from that index. The hint is updated after each search and the
hint can also be mutated from the outside. The hint object is also passed
to the predicate as the third argument. This makes it possible to both
practically eliminate the linear search and to implement the predicate without
allocating extra memory for it.
For example:
L.modify([L.find(R.whereEq({id: 2}), {hint: 2}), 'value'],
R.toUpper,
[{id: 3, value: 'a'},
{id: 2, value: 'b'},
{id: 1, value: 'c'},
{id: 4, value: 'd'},
{id: 5, value: 'e'}])
// [{id: 3, value: 'a'},
// {id: 2, value: 'B'},
// {id: 1, value: 'c'},
// {id: 4, value: 'd'},
// {id: 5, value: 'e'}]
Note that L.find by itself does not satisfy all lens laws. To fix this, you
can e.g. post compose L.find with lenses that ensure that the property being
tested by the predicate given to L.find cannot be written to. See
here for discussion and an example.
L.findWith(optic[, {hint: index}]) ~> optic v1.0.0L.findWith chooses an index from an array-like object through
which the given optic has a non-undefined view and then returns an optic that
focuses on that.
For example:
L.get(L.findWith('x'), [{z: 6}, {x: 9}, {y: 6}])
// 9
L.set(L.findWith('x'), 3, [{z: 6}, {x: 9}, {y: 6}])
// [ { z: 6 }, { x: 3 }, { y: 6 } ]
L.first ~> lens v13.1.0L.first is a synonym for L.index(0) or 0 and
focuses on the first element of an array-like object or works
like L.append in case no such element exists. See also
L.last.
For example:
L.get(L.first, ['a', 'b'])
// 'a'
L.index(elemIndex) ~> lens or elemIndex v1.0.0L.index(elemIndex) or just elemIndex focuses on the element at specified
index of an array-like object.
undefined.undefined, the element is removed from the resulting array,
shifting all higher indices down by one.undefined.For example:
L.set(2, 'z', ['x', 'y', 'c'])
// [ 'x', 'y', 'z' ]
L.remove(0, ['x'])
// [ ]
L.last ~> lens v9.8.0L.last focuses on the last element of an array-like object or
works like L.append in case no such element exists. See also
L.first.
Focusing on an empty array or undefined results in returning undefined. For
example:
L.get(L.last, [1, 2, 3])
// 3
L.get(L.last, [])
// undefined
Setting value with L.last sets the last element of the object or appends the
value if the focused object is empty or undefined. For example:
L.set(L.last, 5, [1, 2, 3])
// [1, 2, 5]
L.set(L.last, 1, [])
// [1]
L.prefix(maybeBegin) ~> lens v11.12.0L.prefix focuses on a range of elements of an array-like object
starting from the beginning of the object. L.prefix is a special case of
L.slice.
The end of the range is determined as follows:
Infinity is the end of the array-like object,-Infinity is the beginning of the array-like object, andundefined is the end of the array-like object.For example:
L.set(L.prefix(0), [1], [2, 3])
// [ 1, 2, 3 ]
L.slice(maybeBegin, maybeEnd) ~> lens v8.1.0L.slice focuses on a specified range of elements of an
array-like object. See also L.prefix and
L.suffix.
The range is determined like with the standard
slice
method of arrays:
Infinity is the end of the array-like object,-Infinity is the beginning of the array-like object, andundefined gives the defaults: 0 for the begin and length for the end.For example:
L.get(L.slice(1, -1), [1, 2, 3, 4])
// [ 2, 3 ]
L.set(L.slice(-2, undefined), [0], [1, 2, 3, 4])
// [ 1, 2, 0 ]
L.suffix(maybeEnd) ~> lens v11.12.0L.suffix focuses on a range of elements of an array-like object
starting from the end of the object. L.suffix is a special case of
L.slice.
The beginning of the range is determined as follows:
Infinity is the beginning of the array-like object,-Infinity is the end of the array-like object, andundefined is the beginning of the array-like object.Note that the rules above are different from the rules for determining the
beginning of L.slice.
For example:
L.set(L.suffix(1), [4, 1], [3, 1, 3])
// [ 3, 1, 4, 1 ]
Anything that is an instanceof Object is considered an object by partial
lenses.
When writing through an optic that operates on objects, the result is always a
plain Object. For example:
function Custom(gold, silver, bronze) {
this.gold = gold
this.silver = silver
this.bronze = bronze
}
L.set('silver', -2, new Custom(1, 2, 3))
// { gold: 1, silver: -2, bronze: 3 }
When manipulating objects whose constructor is not Object,
L.rewrite can be used to convert the result to the desired type,
if necessary:
L.set([L.rewrite(objectTo(Custom)), 'silver'], -2, new Custom(1, 2, 3))
// Custom { gold: 1, silver: -2, bronze: 3 }
Partial lenses also generally guarantees that the creation order of keys is preserved (even though the library used to print out evaluation results from code snippets might not preserve the creation order). For example:
for (const k in L.set('silver', -2, new Custom(1, 2, 3)))
console.log(k)
// gold
// silver
// bronze
When creating new objects, partial lenses generally ignore everything but own string keys. In particular, properties from the prototype chain are not copied and neither are properties with symbol keys.
L.pickIn({prop: lens, ...props}) ~> lens v11.11.0L.pickIn creates a lens from the given possibly nested object template of
lenses similar to L.pick except that the lenses in the template are
relative to their path in the template. This means that using L.pickIn you
can effectively create a kind of filter for a nested object structure. See also
L.props.
For example:
L.get(L.pickIn({meta: {file: [], ext: []}}),
{meta: {file: './foo.txt', base: 'foo', ext: 'txt'}})
// { meta: { file: './foo.txt', ext: 'txt' } }
L.prop(propName) ~> lens or propName v1.0.0L.prop(propName) or just propName focuses on the specified object property.
undefined.Object.undefined, the property is removed from the result.When setting or removing properties, the order of keys is preserved.
For example:
L.get('y', {x: 1, y: 2, z: 3})
// 2
L.set('y', -2, {x: 1, y: 2, z: 3})
// { x: 1, y: -2, z: 3 }
When manipulating objects whose constructor is not Object,
L.rewrite can be used to convert the result to the desired type,
if necessary:
L.set([L.rewrite(objectTo(XYZ)), 'z'], 3, new XYZ(3, 1, 4))
// XYZ { x: 3, y: 1, z: 3 }
L.props(...propNames) ~> lens v1.4.0L.props focuses on a subset of properties of an object, allowing one to treat
the subset of properties as a unit. The view of L.props is undefined when
none of the properties is defined. This allows L.props to be used with
e.g. L.choices. Otherwise the view is an object containing a
subset of the properties. Setting through L.props updates the whole subset of
properties, which means that any missing properties are removed if they did
exists previously. When set, any extra properties are ignored.
L.set(L.props('x', 'y'), {x: 4}, {x: 1, y: 2, z: 3})
// { x: 4, z: 3 }
Note that L.props(k1, ..., kN) is equivalent to L.pick({[k1]: k1, ..., [kN]: kN}) and L.pickIn({[k1]: [], ..., [kN]: []}).
L.propsOf(object) ~> lens v11.13.0L.propsOf(o) is shorthand for L.props(...Object.keys(o))
allowing one to focus on the properties specified via the given sample object.
L.removable(...propNames) ~> lens v9.2.0L.removable creates a lens that, when written through, replaces the whole
result with undefined if none of the given properties is defined in the
written object. L.removable is designed for making removal propagate through
objects.
Contrast the following examples:
L.remove('x', {x: 1, y: 2})
// { y: 2 }
L.remove([L.removable('x'), 'x'], {x: 1, y: 2})
// undefined
Also note that, in a composition, L.removable is likely preceded by
L.valueOr (or L.defaults) like in the
tutorial example. In such a pair, the preceding lens gives a
default value when reading through the lens, allowing one to use such a lens to
insert new objects. The following lens then specifies that removing the then
focused property (or properties) should remove the whole object. In cases where
the shape of the incoming object is know, L.defaults can
replace such a pair.
L.matches(/.../) ~> lens v10.4.0L.matches, when given a regular expression without the
global
flags, /.../, is a partial lens over the match. When there is no match, or
the target is not a string, then L.matches will be read-only. See also
L.matches.
For example:
L.set(L.matches(/\.[^./]+$/),
'.txt',
'/dir/file.ext')
// '/dir/file.txt'
L.valueOr(valueOut) ~> lens v3.5.0L.valueOr is an asymmetric lens used to specify a default value in case the
focus is undefined or null. When set, L.valueOr behaves like the identity
lens.
For example:
L.get(L.valueOr(0), null)
// 0
L.set(L.valueOr(0), 0, 1)
// 0
L.remove(L.valueOr(0), 1)
// undefined
L.pick({prop: lens, ...props}) ~> lens v1.2.0L.pick creates a lens out of the given possibly nested object template of
lenses and allows one to pick apart a data structure and then put it back
together. When viewed, undefined properties are not added to the result and
if the result would be an empty object, the result will be undefined. This
allows L.pick to be used with e.g. L.choices. Otherwise an
object is created, whose properties are obtained by viewing through the lenses
of the template. When set with an object, the properties of the object are set
to the context via the lenses of the template.
For example, let's say we need to deal with data and schema in need of some semantic restructuring:
const sampleFlat = {px: 1, py: 2, vx: 1, vy: 0}
We can use L.pick to create a lens to pick apart the data and put it back
together into a more meaningful structure:
const sanitize = L.pick({pos: {x: 'px', y: 'py'},
vel: {x: 'vx', y: 'vy'}})
Note that in the template object the lenses are relative to the root focus of
L.pick.
We now have a better structured view of the data:
L.get(sanitize, sampleFlat)
// { pos: { x: 1, y: 2 }, vel: { x: 1, y: 0 } }
That works in both directions:
L.modify([sanitize, 'pos', 'x'], R.add(5), sampleFlat)
// { px: 6, py: 2, vx: 1, vy: 0 }
NOTE: In order for a lens created with L.pick to work in a predictable
manner, the given lenses must operate on independent parts of the data
structure. As a trivial example, in L.pick({x: 'same', y: 'same'}) both of
the resulting object properties, x and y, address the same property of the
underlying object, so writing through the lens will give unpredictable results.
Note that, when set, L.pick simply ignores any properties that the given
template doesn't mention. Also note that the underlying data structure need not
be an object.
Note that the sanitize lens defined above can also been seen as an
isomorphism between the "flat" and "nested" forms of the data.
It can even be inverted using L.inverse:
L.get(L.inverse(sanitize), {pos: {x: 1, y: 2}, vel: {x: 1, y: 0}})
// { px: 1, py: 2, vx: 1, vy: 0 }
L.replace(maybeValueIn, maybeValueOut) ~> lens v1.0.0L.replace(maybeValueIn, maybeValueOut), when viewed, replaces the value
maybeValueIn with maybeValueOut and vice versa when set.
For example:
L.get(L.replace(1, 2), 1)
// 2
L.set(L.replace(1, 2), 2, 0)
// 1
The main use case for replace is to handle optional and required properties
and elements. In most cases, rather than using replace, you will make
selective use of defaults, required and
define.
Isomorphisms are lenses with a kind of inverse. The focus of an isomorphism is the whole data structure rather than a part of it.
More specifically, a lens, iso, is an isomorphism if the following equations
hold for all x and y in the domain and range, respectively, of the lens:
L.set(iso, L.get(iso, x), undefined) = x
L.get(iso, L.set(iso, y, undefined)) = y
The above equations mean that x => L.get(iso, x) and y => L.set(iso, y, undefined) are inverses of each other.
That is the general idea. Strictly speaking it is not required that the two functions are precisely inverses of each other. It can be useful to have "isomorphisms" that, when written through, actually change the data structure. For that reason the name "adapter", rather than "isomorphism", is sometimes used for the concept.
In this library there is no type distinction between partial lenses and partial
isomorphisms. Among other things this means that some lens combinators, such as
L.pick, can also be used to create isomorphisms. On the other
hand, some forms of optic composition, particularly adapting and
querying, do not work properly on (inverted) isomorphisms.
L.getInverse(isomorphism, maybeData) ~> maybeData v5.0.0L.getInverse views through an isomorphism in the inverse direction.
For example:
const expect = (p, f) => x => p(x) ? f(x) : undefined
const offBy1 = L.iso(expect(R.is(Number), R.inc),
expect(R.is(Number), R.dec))
L.getInverse(offBy1, 1)
// 0
Note that L.getInverse(iso, data) is equivalent to L.set(iso, data, undefined).
Also note that, while L.getInverse makes most sense when used with an
isomorphism, it is valid to use L.getInverse with partial lenses in general.
Doing so essentially constructs a minimal data structure that contains the given
value. For example:
L.getInverse('meaning', 42)
// { meaning: 42 }
L.iso(maybeData => maybeValue, maybeValue => maybeData) ~> isomorphism v5.3.0L.iso creates a new primitive isomorphism from the given pair of functions.
Usually the given functions should be inverses of each other, but that isn't
strictly necessary. The functions should also be partial so that when the input
doesn't match their expectation, the output is mapped to undefined.
For example:
const reverseString = L.iso(expect(R.is(String), R.reverse),
expect(R.is(String), R.reverse))
L.modify([L.uriComponent,
L.json(),
'bottle',
0,
reverseString,
L.rewrite(R.join('')),
0],
R.toUpper,
'%7B%22bottle%22%3A%5B%22egassem%22%5D%7D')
// '%7B%22bottle%22%3A%22egasseM%22%7D'
L.array(isomorphism) ~> isomorphism v11.19.0L.array lifts an isomorphism between elements, a ≅ b, to an isomorphism
between an array-like object and an array of elements, [a] ≅ [b].
For example:
L.getInverse(L.array(L.pick({x: 'y', z: 'x'})), [{x:2, z:1}, {x:4, z:3}])
// [{x:1, y:2}, {x:3, y:4}]
Elements mapped to undefined by the isomorphism on elements are removed from
the resulting array in both directions.
L.inverse(isomorphism) ~> isomorphism v4.1.0L.inverse returns the inverse of the given isomorphism. Note that this
operation only makes sense on isomorphisms.
For example:
L.get(L.inverse(offBy1), 1)
// 0
L.complement ~> isomorphism v9.7.0L.complement is an isomorphism that performs logical negation of any
non-undefined value when either read or written through.
For example:
L.set([L.complement, L.log()],
'Could be anything truthy',
'Also converted to bool')
// get false
// set 'Could be anything truthy'
// false
L.identity ~> isomorphism v1.3.0L.identity is the identity element of lens composition and also the identity
isomorphism. L.identity can also been seen as specifying an empty path.
Indeed, in this library, when used as an optic, L.identity is equivalent to
[]. The following equations characterize L.identity:
L.get(L.identity, x) = x
L.modify(L.identity, f, x) = f(x)
L.compose(L.identity, l) = l
L.compose(l, L.identity) = l
L.indexed ~> isomorphism v11.21.0L.indexed is an isomorphism between an array-like object and an
array of [index, value] pairs.
For example:
L.modify([L.rewrite(R.join('')),
L.indexed,
L.normalize(R.sortBy(L.get(1))),
0,
1],
R.toUpper,
'optics')
// 'optiCs'
L.is(value) ~> isomorphism v11.1.0L.is reads the given value as true and everything else as false and writes
true as the given value and everything else as undefined. See
here for an example.
L.keyed ~> isomorphism v11.21.0L.keyed is an isomorphism between an object and an array of [key, value]
pairs.
For example:
L.get(L.keyed, {a: 1, b: 2})
// [ ['a', 1], ['b', 2] ]
L.reverse ~> isomorphism v11.22.0L.reverse is an isomorphism between an array-like object
and its reverse.
For example:
L.join(', ', [L.reverse, L.elems], 'abc')
// 'c, b, a'
L.singleton ~> isomorphism v11.18.0L.singleton is a partial isomorphism between an array-like
object, [x], that contains a single element and that element x. When
written through with a non-undefined value, the result is an array containing
the value.
For example:
L.modify(L.singleton, R.negate, [1]) // [-1]
Note that in case the target of L.singleton is an array-like object that does
not contain exactly one element, then the view will be undefined. The reason
for this behaviour is that it allows L.singleton to not only be used to access
the first element of an array-like object, but to also check that the object is
of the expected form.
L.uri ~> isomorphism v11.3.0L.uri is an isomorphism based on the standard
decodeURI
and
encodeURI
functions.
L.uriComponent ~> isomorphism v11.3.0L.uriComponent is an isomorphism based on the standard
decodeURIComponent
and
encodeURIComponent
functions.
L.json({reviver, replacer, space}) ~> isomorphism v11.3.0L.json({reviver, replacer, space}) returns an isomorphism based on the
standard
JSON.parse
and
JSON.stringify
functions. The optional reviver is passed to
JSON.parse
and the optional replacer and space are passed to
JSON.stringify.
For example:
L.transform(
[L.json(), 'foo', L.elems, L.modifyOp(R.negate)],
'{"foo":[3,1,4]}'
)
// '{"foo":[-3,-1,-4]}'
L.dropPrefix(prefix) ~> isomorphism v13.8.0L.dropPrefix drops the given prefix from the beginning of the string when read
through and adds it when written through. In case the input does not contain
the prefix, the result is undefined, which allows L.dropPrefix to be used as
a predicate. See also L.dropSuffix.
For example:
L.get(L.dropPrefix('?'), '?foo=bar')
// 'foo=bar'
L.getInverse(L.dropPrefix('?'), 'foo=bar')
// '?foo=bar'
L.dropSuffix(suffix) ~> isomorphism v13.8.0L.dropSuffix drops the given suffix from the end of the string when read
through and adds it when written through. In case the input does not contain
the suffix, the result is undefined, which allows L.dropSuffix to be used as
a predicate. See also L.dropPrefix.
For example:
L.get(L.dropSuffix('.bar'), 'foo.bar')
// 'foo'
L.getInverse(L.dropSuffix('.bar'), 'foo')
// 'foo.bar'
L.replaces(substringIn, substringOut) ~> isomorphism v13.8.0L.replaces replaces substrings in the string passing through both when read
and written.
For example:
L.get(L.replaces('+', ' '), 'Is+this too+much?')
// 'Is this too much?'
L.getInverse(L.replaces('+', ' '), 'Is URL+encoding fun?')
// 'Is+URL+encoding+fun?'
L.split(separator[, separatorRegExp]) ~> isomorphism v13.8.0L.split splits a string with given separator into an array when read through
and joins an array of strings into a string with the separator when written
through. The second argument to L.split is optional and specifies the pattern
to be used for splitting instead of the default separator string. See also
L.uncouple.
For example:
L.get(L.split(',', /\s*,\s*/), 'comma, separated, items')
// ['comma', 'separated', 'items']
L.getInverse(L.split('&'), ['roses=red', 'violets=blue', 'sugar=sweet'])
// 'roses=red&violets=blue&sugar=sweet'
L.uncouple(separator[, separatorRegExp]) ~> isomorphism v13.8.0L.uncouple splits a string with the given separator into a pair when read
through and joins a pair of strings into a string with the separator when
written through. In case the input string does not contain the separator, the
second element of the pair will be an empty string. Likewise, if the second
element of the pair is an empty string, no separator is written to the resulting
string. The second argument to L.uncouple is optional and specifies the
pattern to be used for splitting instead of the default separator string. See
also L.split.
For example:
L.get(L.uncouple('=', /\s*=\s*/), 'foo = bar')
// [ 'foo', 'bar' ]
L.getInverse(L.uncouple('='), ['key', ''])
// 'key'
L.add(number) ~> isomorphism v13.9.0L.add adds the given constant to the number in focus when read through and
subtracts when written through.
For example:
L.get(L.add(1), 2)
// 3
L.divide(number) ~> isomorphism v13.9.0L.divide divides the number in focus by the given constant when read through
and multiplies when written through.
For example:
L.get(L.divide(2), 6)
// 3
L.multiply(number) ~> isomorphism v13.9.0L.multiply multiplies the number in focus by the given constant when read
through and divides when written through.
For example:
L.get(L.multiply(2), 3)
// 6
L.negate ~> isomorphism v13.9.0L.negate negates the number in focus when either read or written through.
For example:
L.get(L.negate, 2)
// -2
L.subtract(number) ~> isomorphism v13.9.0L.subtract subtracts the given constant from the number in focus when read
through and adds when written through.
For example:
L.get(L.subtract(1), 3)
// 2
L.pointer(jsonPointer) ~> lens v11.21.0L.pointer converts a valid JSON Pointer
(string) into a bidirectional lens. Works with JSON
String and URI Fragment
Identifier representations.
For Example:
L.get(L.pointer('/foo/0'), {foo: [1, 2]})
// 1
L.modify(L.pointer('#/foo/1'), x => x + 1, {foo: [1, 2]})
// {foo: [1, 3]}
L.seemsArrayLike(anything) ~> boolean v11.4.0L.seemsArrayLike determines whether the given value is an instanceof Object
that has a non-negative integer length property or a string, which are not
Objects in JavaScript. In this library, such values are considered
array-like objects that can be manipulated with various optics.
Note that this function is intentionally loose, which is also intentionally apparent from the name of this function. JavaScript includes many array-like values, including normal arrays, typed arrays, and strings. Unfortunately there seems to be no simple way to directly and precisely test for all of those. Testing explicitly for every standard variation would be costly and might not cover user defined types. Fortunately, optics are targeting specific paths inside data-structures, rather than completely arbitrary values, which means that even a loose test can be accurate enough.
Note that if you are new to lenses, then you probably want to start with the tutorial.
A case that we have run into multiple times is where we have an array of constant strings that we wish to manipulate as if it was a collection of boolean flags:
const sampleFlags = ['id-19', 'id-76']
Here is a parameterized lens that does just that:
const flag = id => [L.normalize(R.sortBy(R.identity)),
L.find(R.equals(id)),
L.is(id)]
Now we can treat individual constants as boolean flags:
L.get(flag('id-69'), sampleFlags)
// false
L.get(flag('id-76'), sampleFlags)
// true
In both directions:
L.set(flag('id-69'), true, sampleFlags)
// ['id-19', 'id-69', 'id-76']
L.set(flag('id-76'), false, sampleFlags)
// ['id-19']
It is not atypical to have UIs where one selection has an effect on other
selections. For example, you could have an UI where you can specify maximum
and initial values for some measure and the idea is that the initial value
cannot be greater than the maximum value. One way to deal with this
requirement is to implement it in the lenses that are used to access the
maximum and initial values. This way the UI components that allows the user
to edit those values can be dumb and do not need to know about the restrictions.
One way to build such a lens is to use a combination of L.props
(or, in more complex cases, L.pick) to limit the set of properties
to deal with, and L.rewrite to insert the desired restriction
logic. Here is how it could look like for the maximum:
const maximum = [
L.props('maximum', 'initial'),
L.rewrite(props => {
const {maximum, initial} = props
if (maximum < initial)
return {maximum, initial: maximum}
else
return props
}),
'maximum']
Now:
L.set(maximum,
5,
{maximum: 10, initial: 8, something: 'else'})
// {maximum: 5, initial: 5, something: 'else'}
A typical element of UIs that display a list of selectable items is a checkbox to select or unselect all items. For example, the TodoMVC spec includes such a checkbox. The state of a checkbox is a single boolean. How do we create a lens that transforms a collection of booleans into a single boolean?
The state of a todo list contains a boolean completed flag per item:
const sampleTodos = [{completed: true}, {completed: false}, {completed: true}]
We can address those flags with a traversal:
const completedFlags = [L.elems, 'completed']
To compute a single boolean out of a traversal over booleans we can use the
L.and fold and use that to define a lens parameterized over flag
traversals using L.foldTraversalLens:
const selectAll = L.foldTraversalLens(L.and)
Now we can say, for example:
L.get(selectAll(completedFlags), sampleTodos)
// false
L.set(selectAll(completedFlags), true, sampleTodos)
// [{completed: true}, {completed: true}, {completed: true}]
As an exercise define unselectAll using the L.or fold. How does it
differ from selectAll?
Binary search trees might initially seem to be outside the scope of definable lenses. However, given basic BST operations, one could easily wrap them as a primitive partial lens. But could we leverage lens combinators to build a BST lens more compositionally?
We can. The L.cond combinator allows for dynamic selection of
lenses based on examining the data structure being manipulated. Using
L.cond we can write the ordinary BST logic to pick the correct
branch based on the key in the currently examined node and the key that we are
looking for. So, here is our first attempt at a BST lens:
const searchAttempt = key => L.lazy(rec => [
L.cond([n => !n || key === n.key, L.defaults({key})],
[n => key < n.key, ['smaller', rec]],
[ ['greater', rec]])])
const valueOfAttempt = key => [searchAttempt(key), 'value']
Note that we also make use of the L.lazy combinator to create a
recursive lens with a cyclic representation.
This actually works to a degree. We can use the valueOfAttempt lens
constructor to build a binary tree. Here is a little helper to build a tree
from pairs:
const fromPairs =
R.reduce((t, [k, v]) => L.set(valueOfAttempt(k), v, t), undefined)
Now:
const sampleBST = fromPairs([[3, 'g'], [2, 'a'], [1, 'm'], [4, 'i'], [5, 'c']])
sampleBST
// { key: 3,
// value: 'g',
// smaller: { key: 2, value: 'a', smaller: { key: 1, value: 'm' } },
// greater: { key: 4, value: 'i', greater: { key: 5, value: 'c' } } }
However, the above searchAttempt lens constructor does not maintain the BST
structure when values are being removed:
L.remove(valueOfAttempt(3), sampleBST)
// { key: 3,
// smaller: { key: 2, value: 'a', smaller: { key: 1, value: 'm' } },
// greater: { key: 4, value: 'i', greater: { key: 5, value: 'c' } } }
How do we fix this? We could check and transform the data structure to a BST
after changes. The L.rewrite combinator can be used for that
purpose. Here is a naïve rewrite to fix a tree after value removal:
const naiveBST = L.rewrite(n => {
if (undefined !== n.value) return n
const s = n.smaller, g = n.greater
if (!s) return g
if (!g) return s
return L.set(search(s.key), s, g)
})
Here is a working search lens and a valueOf lens constructor:
const search = key => L.lazy(rec => [
naiveBST,
L.cond([n => !n || key === n.key, L.defaults({key})],
[n => key < n.key, ['smaller', rec]],
[ ['greater', rec]])])
const valueOf = key => [search(key), 'value']
Now we can also remove values from a binary tree:
L.remove(valueOf(3), sampleBST)
// { key: 4,
// value: 'i',
// greater: { key: 5, value: 'c' },
// smaller: { key: 2, value: 'a', smaller: { key: 1, value: 'm' } } }
As an exercise, you could improve the rewrite to better maintain balance.
Perhaps you might even enhance it to maintain a balance condition such as
AVL or
Red-Black. Another
worthy exercise would be to make it so that the empty binary tree is null
rather than undefined.
What about traversals over BSTs? We can use the
L.branch combinator to define an in-order traversal over the
values of a BST:
const values = L.lazy(rec => [
L.optional,
naiveBST,
L.branch({smaller: rec,
value: L.identity,
greater: rec})])
Given a binary tree sampleBST we can now manipulate it as a whole. For
example:
L.join('-', values, sampleBST)
// 'm-a-g-i-c'
L.modify(values, R.toUpper, sampleBST)
// { key: 3,
// value: 'G',
// smaller: { key: 2, value: 'A', smaller: { key: 1, value: 'M' } },
// greater: { key: 4, value: 'I', greater: { key: 5, value: 'C' } } }
L.remove([values, L.when(x => x > 'e')], sampleBST)
// { key: 5, value: 'c', smaller: { key: 2, value: 'a' } }
Immutable.js is a popular library providing immutable data structures. As argued in Lenses with Immutable.js it can be useful to be able to manipulate Immutable.js data structures using optics.
When interfacing external libraries with partial lenses one does need to consider whether and how to support partiality. Partial lenses allow one to insert new and remove existing elements rather than just view and update existing elements.
List indexingHere is a primitive partial lens for indexing
List written using
L.lens:
const getList = i => xs => Immutable.List.isList(xs) ? xs.get(i) : undefined
const setList = i => (x, xs) => {
if (!Immutable.List.isList(xs))
xs = Immutable.List()
if (x !== undefined)
return xs.set(i, x)
return xs.delete(i)
}
const idxList = i => L.lens(getList(i), setList(i))
Note how the above uses isList to check the input. When viewing, in case the
input is not a List, the proper result is undefined. When updating the
proper way to handle a non-List is to treat it as empty. Also, when updating,
we treat undefined as a request to delete rather than set.
We can now view existing elements:
const sampleList = Immutable.List(['a', 'l', 'i', 's', 't'])
L.get(idxList(2), sampleList)
// 'i'
Update existing elements:
L.modify(idxList(1), R.toUpper, sampleList)
// List [ 'a', 'L', 'i', 's', 't' ]
And remove existing elements:
L.remove(idxList(0), sampleList)
// List [ 'l', 'i', 's', 't' ]
We can also create lists from non-lists:
L.set(idxList(0), 'x', undefined)
// List [ 'x' ]
And we can also append new elements:
L.set(idxList(5), '!', sampleList)
// List [ 'a', 'l', 'i', 's', 't', '!' ]
Consider what happens when the index given to idxList points further beyond
the last element. Both the L.index lens and the above lens add
undefined values, which is not ideal with partial lenses, because of the
special treatment of undefined. In practise, however, it is not typical to
set elements except to append just after the last element.
Fortunately we do not need Immutable.js data structures to provide a compatible
partial
traverse
function to support traversals, because it is also possible to
implement traversals simply by providing suitable isomorphisms between
Immutable.js data structures and JSON. Here is a partial
isomorphism between List and arrays:
const fromList = xs => Immutable.List.isList(xs) ? xs.toArray() : undefined
const toList = xs => R.is(Array, xs) && xs.length ? Immutable.List(xs) : undefined
const isoList = L.iso(fromList, toList)
So, now we can compose a traversal over List as:
const seqList = [isoList, L.elems]
And all the usual operations work as one would expect, for example:
L.remove([seqList, L.when(c => c < 'i')], sampleList)
// List [ 'l', 's', 't' ]
And:
L.joinAs(R.toUpper,
'',
[seqList, L.when(c => c <= 'i')],
sampleList)
// 'AI'
L.filter, L.find, L.select, and L.whenThe L.filter, L.find, L.select, and
L.when serve related, but different, purposes and it is important
to understand their differences in order to make best use of them.
Here is a table of their call patterns and type signatures:
| Call pattern | Type signature |
|---|---|
L.filter((value, index) => bool) ~> lens | L.filter: ((Maybe a, Index) -> Boolean) -> PLens [a] [a] |
L.find((value, index) => bool) ~> lens | L.find: ((Maybe a, Index) -> Boolean) -> PLens [a] a |
L.select(traversal, data) ~> value | L.select: PTraversal s a -> Maybe s -> Maybe a |
L.when((value, index) => bool) ~> optic | L.when: ((Maybe a, Index) -> Boolean) -> POptic a a |
As can be read from above, both L.filter and L.find
introduce lenses, L.select eliminates a traversal, and
L.when introduces an optic, which will always be a traversal in
this section. We can also read that L.filter and
L.find operate on arrays, while L.select and
L.when operate on arbitrary traversals. Yet another thing to make
note of is that both L.find and L.select are
many-to-one while both L.filter and L.when retain
cardinality.
The following equations relate the operations in the read direction:
L.get([L.filter(p), 0]) = L.get(L.find(p))
L.select([L.elems, L.when(p)]) = L.get(L.find(p))
L.collect([L.elems, L.when(p)]) = L.get(L.filter(p))
In the write direction there are no such simple equations.
L.find can be used to create a bidirectional view of an element in
an array identified by a given predicate. Despite the name, L.find
is probably not what one should use to generally search for something in a data
structure.
L.select (and L.selectAs) can be used to search
for an element in a data structure following an arbitrary traversal. That
traversal can, of course, also make use of L.when to filter elements
or to limit the traversal.
L.filter can be used to create a bidirectional view of a subset
of elements of an array matching a given predicate. L.filter
should probably be the least most commonly used of the bunch. If the end goal
is simply to manipulate multiple elements, it is preferable to use a combination
of L.elems and L.when, because then no intermediate
array of the elements is
computed.
Traversals do not materialize intermediate aggregates and it is useful to understand this performance characteristic.
Consider the following naïve use of Ramda:
const sumPositiveXs = R.pipe(R.flatten,
R.map(R.prop('x')),
R.filter(R.lt(0)),
R.sum)
const sampleXs = [[{x: 1}], [{x: -2}, {x: 2}]]
sumPositiveXs(sampleXs)
// 3
A performance problem in the above naïve sumPositiveXs function is that aside
from the last step, R.sum, every step of the computation, R.flatten,
R.map(R.prop('x')), and R.filter(R.lt(0)), creates an intermediate array
that is only used by the next step of the computation and is then thrown away.
When dealing with large amounts of data this kind of composition can cause
performance issues.
Please note that the above example is intentionally naïve. In Ramda one can
use transducers to avoid building such intermediate
results although in
this particular case the use of R.flatten
makes things a bit more interesting, because it doesn't (at the time of writing)
act as a transducer in Ramda (version 0.24.1).
Using traversals one could perform the same summations as
L.sum([L.flatten, 'x', L.when(R.lt(0))], sampleXs)
// 3
and, thankfully, it doesn't create intermediate arrays. This is the case with traversals in general.
L.chooseThe function given to L.choose is called each time the optic is
used and any allocations done by the function are consequently repeated.
Consider the following example:
L.choose(x => Array.isArray(x) ? [L.elems, 'data'] : 'data')
A performance issue with the above is that each time it is used on an array, a
new composition, [L.elems, 'data'], is allocated. Performance may be improved
by moving the allocation outside of L.choose:
const onArray = [L.elems, 'data']
L.choose(x => Array.isArray(x) ? onArray : 'data')
In cases like above you can also use the more restricted L.cond
combinator:
L.cond([Array.isArray, [L.elems, 'data']], ['data'])
This has the advantage that the optics are constructed only once.
The distribution of this library includes a prebuilt and minified browser
bundle. However,
this library is not designed to be primarily used via that bundle. Rather, this
library is bundled with Rollup, uses /*#__PURE__*/
annotations to help UglifyJS do better
dead code elimination, and uses process.env.NODE_ENV to detect 'production'
mode to discard some warnings and error checks. This means that when using
Rollup with replace and
uglify plugins to build
browser bundles, the generated bundles will basically only include what you use
from this library.
For best results, increasing the number of compression passes may allow UglifyJS to eliminate more dead code. Here is a sample snippet from a Rollup config:
import replace from 'rollup-plugin-replace'
import uglify from 'rollup-plugin-uglify'
// ...
export default {
plugins: [
replace({
'process.env.NODE_ENV': JSON.stringify('production')
}),
// ...
uglify({
compress: {
passes: 3
}
})
]
}
In late 2015, while implementing UIs for manipulating fairly complex JSON objects, we wrote a module of additional lens combinators on top of Ramda's lenses. Lenses allowed us to operate on nested objects in a compositional manner and, thanks to treating data as immutable, also made it easy to provide undo-redo. Pretty quickly, however, it became evident that Ramda's support for lenses left room for improvement.
First of all, upto and including Ramda version 0.24.1, Ramda's lenses didn't deal with non-existent focuses consistently:
R.view(R.lensPath(['x', 'y']), {})
// undefined
R.view(R.compose(R.lensProp('x'), R.lensProp('y')), {})
// TypeError: Cannot read property 'y' of undefined
(In Ramda version 0.25.0, roughly two years later, both of the above now
return undefined.)
In addition to using lenses to view and set, we also wanted to have the ability to insert and remove. In other words, we wanted full CRUD semantics, because that is what our UIs also had to provide.
We also wanted lenses to have the ability to search for things, because we often had to deal with e.g. arrays containing objects with unique IDs aka association lists.
All of these considerations give rise to a notion of partiality, which is what the Partial Lenses library set out to explore in early 2016. Since then the library has grown to a comprehensive, high-performance, optics library, supporting not only partial lenses, but also isomorphisms, traversals, and also a notion of transforms.
There are several lens and optics libraries for JavaScript. In this section I'd like to very briefly elaborate on a number design choices made during the course of developing this library.
Making all optics partial allows optics to not only view and update existing elements, but also to insert, replace (as in replace with data of different type) and remove elements and to do so in a seamless and efficient way. In a library based on total lenses, one needs to e.g. explicitly compose lenses with prisms to deal with partiality. This not only makes the optic compositions more complex, but can also have a significant negative effect on performance.
The downside of implicit partiality is the potential to create incorrect optics that signal errors later than when using total optics.
JSON is the data-interchange format of choice today. By being able to effectively and efficiently manipulate JSON data structures directly, one can avoid using special internal representations of data and make things simpler (e.g. no need to convert from JSON to efficient immutable collections and back).
undefinedundefined is a natural choice in JavaScript, especially when dealing with
JSON, to represent nothingness. Some libraries use null, but that is arguably
a poor choice, because null is a valid JSON value. Some libraries implement
special Maybe types, but the benefits do not seem worth the trouble. First of
all, undefined already exists in JavaScript and is not a valid JSON value.
Inventing a new value to represent nothingness doesn't seem to add much. OTOH,
wrapping values with Just objects introduces a significant performance
overhead due to extra allocations. Operations with optics do not otherwise
necessarily require large numbers of allocations and can be made highly
efficient.
Not having an explicit Just object means that dealing with values such as
Just Nothing requires special consideration.
Aside from the brevity, allowing strings and non-negative integers to be directly used as optics allows one to avoid allocating closures for such optics. This can provide significant time and, more importantly, space savings in applications that create large numbers of lenses to address elements in data structures.
The downside of allowing such special values as optics is that the internal implementation needs to be careful to deal with them at any point a user given value needs to be interpreted as an optic.
Aside from the brevity, treating an array of optics as a
composition allows the library to be optimized to deal with simple
paths highly efficiently and eliminate the need for separate primitives like
assocPath and
dissocPath for performance reasons.
Client code can also manipulate such simple paths as data.
One interesting consequence of partiality is that it becomes possible to invert isomorphisms without explicitly making it possible to extract the forward and backward functions from an isomorphism. A simple internal implementation based on functors and applicatives seems to be expressive enough for a wide variety of operations.
By providing combinators for creating new traversals,
lenses and isomorphisms, client code need not depend on the
internal implementation of optics. The current version of this library exposes
the internal implementation via L.toFunction, but it would
not be unreasonable to not provide such an operation. Only very few
applications need to know the internal representation of optics.
Indexing in partial lenses is unnested, very simple and based on the indices and keys of the underlying data structures. When indexing was added, it essentially introduced no performance degradation, but since then a few operations have been added that do require extra allocations to support indexing. It is also possible to compose optics so as to create nested indices or paths, but currently no combinator is directly provided for that.
The algebraic structures used in partial lenses follow the Static Land specification rather than the Fantasy Land specification. Static Land does not require wrapping values in objects, which translates to a significant performance advantage throughout the library, because fewer allocations are required.
However, the original
reason
for switching to use Static Land was that correct
implementation of traverse requires the
ability to construct a value of a given applicative type without having any
instance of said applicative type. This means that one has to explicitly pass
something, e.g. a function of, through optics to make that possible. This
eliminates a major notational advantage of Fantasy Land. In Static Land, which
can basically be seen as using the dictionary translation of type classes, one
already passes the algebra module to combinators.
Concern for performance has been a part of the work on partial lenses for some time. The basic principles can be summarized in order of importance:
Here are a few benchmark results on partial lenses (as L version 13.1.1) with
Node.js v8.9.3 and some roughly equivalent operations using
Ramda (as R version 0.25.0), Ramda
Lens (as P version 0.1.2), Flunc
Optics (as O version 0.0.2),
Optika (as K version 0.0.2),
lodash.get (as _get version
4.4.2), and unchanged (as U
version 1.0.4). As always with benchmarks, you should take these numbers with a
pinch of salt and preferably try and measure your actual use cases!
29,261,559/s 1.00 L.get(L_find_id_5000, ids)
6,263,306/s 1.00 R.reduceRight(add, 0, xs100)
702,855/s 8.91 L.foldr(add, 0, L.elems, xs100)
223,260/s 28.05 xs100.reduceRight(add, 0)
3,516/s 1781.23 O.Fold.foldrOf(O.Traversal.traversed, addC, 0, xs100)
11,221/s 1.00 R.reduceRight(add, 0, xs100000)
242/s 46.28 L.foldr(add, 0, L.elems, xs100000)
61/s 183.44 xs100000.reduceRight(add, 0)
0/s Infinity O.Fold.foldrOf(O.Traversal.traversed, addC, 0, xs100000) -- STACK OVERFLOW
5,768,818/s 1.00 {let s=0; for (let i=0; i<xs100.length; ++i) s+=xs100[i]; return s}
3,966,543/s 1.45 L.sum(L.elems, xs100)
1,761,821/s 3.27 K.traversed().sumOf(xs100)
1,088,094/s 5.30 L.foldl(add, 0, L.elems, xs100)
1,028,546/s 5.61 xs100.reduce(add, 0)
559,221/s 10.32 L.concat(Sum, L.elems, xs100)
43,679/s 132.07 R.reduce(add, 0, xs100)
39,374/s 146.51 R.sum(xs100)
19,643/s 293.68 P.sumOf(P.traversed, xs100)
3,972/s 1452.40 O.Fold.sumOf(O.Traversal.traversed, xs100)
2,502/s 2305.79 O.Fold.foldlOf(O.Traversal.traversed, addC, 0, xs100)
1,191,166/s 1.00 L.maximum(L.elems, xs100)
2,880/s 413.63 O.Fold.maximumOf(O.Traversal.traversed, xs100)
637,283/s 1.00 {let s=0; for (let i=0; i<xsss100.length; ++i) for (let j=0, xss=xsss100[i]; j<xss.length; ++j) for (let k=0, xs=xss[j]; k<xs.length; ++k) s+=xs[i]; return s}
322,280/s 1.98 K_t_t_t.sumOf(xsss100)
266,188/s 2.39 L.foldl(add, 0, L_e_e_e, xsss100)
251,599/s 2.53 L.foldl(add, 0, [L.elems, L.elems, L.elems], xsss100)
182,952/s 3.48 K.traversed().traversed().traversed().sumOf(xsss100)
164,781/s 3.87 L.sum(L_e_e_e, xsss100)
159,784/s 3.99 L.sum([L.elems, L.elems, L.elems], xsss100)
157,992/s 4.03 L.concat(Sum, [L.elems, L.elems, L.elems], xsss100)
4,281/s 148.86 P.sumOf(R.compose(P.traversed, P.traversed, P.traversed), xsss100)
804/s 792.17 O.Fold.sumOf(R.compose(O.Traversal.traversed, O.Traversal.traversed, O.Traversal.traversed), xsss100)
2,493,770/s 1.00 K.traversed().arrayOf(xs100)
973,139/s 2.56 L.collect(L.elems, xs100)
784,513/s 3.18 xs100.map(I.id)
3,034/s 821.88 O.Fold.toListOf(O.Traversal.traversed, xs100)
250,527/s 1.00 L.collect(L_e_e_e, xsss100)
237,554/s 1.05 L.collect([L.elems, L.elems, L.elems], xsss100)
44,751/s 5.60 {let acc=[]; xsss100.forEach(x0 => {x0.forEach(x1 => {acc = acc.concat(x1)})}); return acc}
38,308/s 6.54 K_t_t_t.arrayOf(xsss100)
35,206/s 7.12 K.traversed().traversed().traversed().arrayOf(xsss100)
9,223/s 27.16 R.chain(R.chain(R.identity), xsss100)
735/s 341.03 O.Fold.toListOf(R.compose(O.Traversal.traversed, O.Traversal.traversed, O.Traversal.traversed), xsss100)
61,367/s 1.00 L.collect(L.flatten, xsss100)
21,566/s 2.85 R.flatten(xsss100)
15,709,764/s 1.00 xs.map(inc)
14,296,101/s 1.10 L.modify(L.elems, inc, xs)
2,992,297/s 5.25 R.map(inc, xs)
1,470,281/s 10.68 K.traversed().over(xs, inc)
508,177/s 30.91 O.Setter.over(O.Traversal.traversed, inc, xs)
323,509/s 48.56 P.over(P.traversed, inc, xs)
531,273/s 1.00 L.modify(L.elems, inc, xs1000)
91,098/s 5.83 xs1000.map(inc)
85,445/s 6.22 R.map(inc, xs1000)
84,705/s 6.27 K.traversed().over(xs1000, inc)
379/s 1400.14 O.Setter.over(O.Traversal.traversed, inc, xs1000) -- QUADRATIC
350/s 1518.84 P.over(P.traversed, inc, xs1000) -- QUADRATIC
193,914/s 1.00 L.modify(L_e_e_e, inc, xsss100)
178,651/s 1.09 L.modify([L.elems, L.elems, L.elems], inc, xsss100)
100,368/s 1.93 K_t_t_t.over(xsss100, inc)
88,725/s 2.19 K.traversed().traversed().traversed().over(xsss100, inc)
86,297/s 2.25 xsss100.map(x0 => x0.map(x1 => x1.map(inc)))
11,834/s 16.39 R.map(R.map(R.map(inc)), xsss100)
3,583/s 54.12 O.Setter.over(R.compose(O.Traversal.traversed, O.Traversal.traversed, O.Traversal.traversed), inc, xsss100)
2,859/s 67.82 P.over(R.compose(P.traversed, P.traversed, P.traversed), inc, xsss100)
51,874,299/s 1.00 L.get(1, xs)
35,680,586/s 1.45 _get(xs, 1)
19,954,170/s 2.60 U.get(1, xs)
13,182,372/s 3.94 R.nth(1, xs)
1,956,697/s 26.51 R.view(l_1, xs)
1,419,735/s 36.54 K.idx(1).get(xs)
154,267,077/s 1.00 L_get_1(xs)
18,509,602/s 8.33 L.get(1)(xs)
5,174,261/s 29.81 R_nth_1(xs)
3,140,154/s 49.13 R.nth(1)(xs)
2,969,585/s 51.95 U_get_1(xs)
2,415,058/s 63.88 U.get(1)(xs)
31,500,628/s 1.00 L.set(1, 0, xs)
9,391,877/s 3.35 xs.map((x, i) => i === 1 ? 0 : x)
7,110,172/s 4.43 {let ys = xs.slice(); ys[1] = 0; return ys}
5,074,836/s 6.21 U.set(1, 0, xs)
3,072,405/s 10.25 R.update(1, 0, xs)
947,676/s 33.24 K.idx(1).set(xs, 0)
815,287/s 38.64 R.set(l_1, 0, xs)
38,524,625/s 1.00 L.get('y', xyz)
17,349,278/s 2.22 _get(xyz, 'y')
16,429,516/s 2.34 U.get('y', xyz)
9,193,603/s 4.19 R.prop('y', xyz)
1,770,509/s 21.76 R.view(l_y, xyz)
1,434,326/s 26.86 K.key('y').get(xyz)
68,577,224/s 1.00 L_get_y(xyz)
15,435,254/s 4.44 L.get('y')(xyz)
4,702,316/s 14.58 R_prop_y(xyz)
2,821,439/s 24.31 U_get_y(xyz)
2,774,587/s 24.72 R.prop('y')(xyz)
2,304,145/s 29.76 U.get('y')(xyz)
7,450,898/s 1.00 R.assoc('y', 0, xyz)
7,322,941/s 1.02 L.set('y', 0, xyz)
1,895,793/s 3.93 U.set('y', 0, xyz)
995,035/s 7.49 K.key('y').set(xyz, 0)
875,025/s 8.52 R.set(l_y, 0, xyz)
12,154,904/s 1.00 _get(axay, [0, 'x', 0, 'y'])
11,297,478/s 1.08 L.get([0, 'x', 0, 'y'], axay)
10,140,829/s 1.20 R.path([0, 'x', 0, 'y'], axay)
4,275,282/s 2.84 U.get([0, 'x', 0, 'y'], axay)
1,706,187/s 7.12 R.view(l_0x0y, axay)
767,316/s 15.84 K_0_x_0_y.get(axay)
492,426/s 24.68 R.view(l_0_x_0_y, axay)
3,635,072/s 1.00 L.set([0, 'x', 0, 'y'], 0, axay)
931,074/s 3.90 U.set([0, 'x', 0, 'y'], 0, axay)
741,621/s 4.90 R.assocPath([0, 'x', 0, 'y'], 0, axay)
573,987/s 6.33 K_0_x_0_y.set(axay, 0)
398,742/s 9.12 R.set(l_0x0y, 0, axay)
266,083/s 13.66 R.set(l_0_x_0_y, 0, axay)
3,571,529/s 1.00 L.modify([0, 'x', 0, 'y'], inc, axay)
578,551/s 6.17 K_0_x_0_y.over(axay, inc)
453,113/s 7.88 R.over(l_0x0y, inc, axay)
285,952/s 12.49 R.over(l_0_x_0_y, inc, axay)
31,022,872/s 1.00 L.remove(1, xs)
3,430,687/s 9.04 R.remove(1, 1, xs)
3,029,069/s 10.24 U.remove(1, xs)
7,992,802/s 1.00 L.remove('y', xyz)
2,435,349/s 3.28 R.dissoc('y', xyz)
1,196,219/s 6.68 U.remove('y', xyz)
19,206,167/s 1.00 _get(xyzn, ['x', 'y', 'z'])
12,018,401/s 1.60 L.get(['x', 'y', 'z'], xyzn)
10,435,414/s 1.84 R.path(['x', 'y', 'z'], xyzn)
4,598,735/s 4.18 U.get(['x', 'y', 'z'], xyzn)
1,881,768/s 10.21 R.view(l_xyz, xyzn)
848,943/s 22.62 K_xyz.get(xyzn)
683,515/s 28.10 R.view(l_x_y_z, xyzn)
154,207/s 124.55 O.Getter.view(o_x_y_z, xyzn)
3,864,421/s 1.00 L.set(['x', 'y', 'z'], 0, xyzn)
1,068,844/s 3.62 U.set(['x', 'y', 'z'], 0, xyzn)
1,066,246/s 3.62 R.assocPath(['x', 'y', 'z'], 0, xyzn)
672,562/s 5.75 K_xyz.set(xyzn, 0)
499,486/s 7.74 R.set(l_xyz, 0, xyzn)
398,131/s 9.71 R.set(l_x_y_z, 0, xyzn)
200,548/s 19.27 O.Setter.set(o_x_y_z, 0, xyzn)
1,280,471/s 1.00 R.find(x => x > 3, xs100)
1,066,129/s 1.20 L.selectAs(x => x > 3 ? x : undefined, L.elems, xs100)
2,529/s 506.25 O.Fold.findOf(O.Traversal.traversed, x => x > 3, xs100)
9,325,674/s 1.00 L.selectAs(x => x < 3 ? x : undefined, L.elems, xs100)
4,411,876/s 2.11 R.find(x => x < 3, xs100)
2,473/s 3770.86 O.Fold.findOf(O.Traversal.traversed, x => x < 3, xs100) -- NO SHORTCUT EVALUATION
10,090/s 1.00 L.sum([L.elems, x => x+1, x => x*2, L.when(x => x%2 === 0)], xs1000)
3,838/s 2.63 R.transduce(R.compose(R.map(x => x+1), R.map(x => x*2), R.filter(x => x%2 === 0)), (x, y) => x+y, 0, xs1000)
3,166/s 3.19 R.pipe(R.map(x => x+1), R.map(x => x*2), R.filter(x => x%2 === 0), R.sum)(xs1000)
216,761/s 1.00 R.forEach(I.id, xs1000)
190,861/s 1.14 L.forEach(I.id, L.elems, xs1000)
115,582/s 1.88 xs1000.forEach(I.id)
252,911/s 1.00 L.forEach(I.id, L_e_e_e, xsss100)
237,600/s 1.06 L.forEach(I.id, [L.elems, L.elems, L.elems], xsss100)
99,597/s 2.54 xsss100.forEach(xss100 => xss100.forEach(xs100 => xs100.forEach(I.id)))
29,031/s 8.71 R.forEach(R.forEach(R.forEach(I.id)), xsss100)
5,717/s 1.00 L.minimum(L.elems, xs10000)
5,670/s 1.01 L.minimumBy(x => -x, L.elems, xs10000)
3,464/s 1.65 R.reduceRight(R.min, -Infinity, xs10000)
2,330/s 2.45 R.reduce(R.min, -Infinity, xs10000)
2,319/s 2.47 R.reduceRight(R.minBy(x => -x), Infinity, xs10000)
1,761/s 3.25 R.reduce(R.minBy(x => -x), Infinity, xs10000)
149,352/s 1.00 L.mean(L.elems, xs1000)
3,882/s 38.48 R.mean(xs1000)
5,768,842/s 1.00 L.remove(50, xs100)
1,766,663/s 3.27 R.remove(50, 1, xs100)
5,097,235/s 1.00 L.set(50, 2, xs100)
1,468,277/s 3.47 R.update(50, 2, xs100)
761,548/s 6.69 K.idx(50).set(xs100, 2)
583,231/s 8.74 R.set(l_50, 2, xs100)
75,197/s 1.00 L.remove(5000, xs10000)
38,157/s 1.97 R.remove(5000, 1, xs10000)
62,694/s 1.00 L.set(5000, 2, xs10000)
25,116/s 2.50 R.update(5000, 2, xs10000)
6,126,231/s 1.00 L.modify(L.values, inc, xyz)
382,949/s 1.00 L.modify(L.values, inc, xs10o)
46,114/s 8.30 L.modify(L.values, inc, xs100o)
4,858/s 78.83 L.modify(L.values, inc, xs1000o)
464/s 825.35 L.modify(L.values, inc, xs10000o)
645,308/s 1.00 L.modify(flatten, inc, nested)
373,998/s 1.73 L.modify(everywhere, incNum, nested)
937,120/s 1.00 L.modify(flatten, inc, xs10)
804,249/s 1.17 L.modify(everywhere, incNum, xs10)
156,861/s 1.00 L.modify(flatten, inc, xs100)
151,030/s 1.04 L.modify(everywhere, incNum, xs100)
17,261/s 1.00 L.modify(flatten, inc, xs1000)
16,558/s 1.04 L.modify(everywhere, incNum, xs1000)
1,618,143/s 1.00 L.set(xyzs, 1, undefined)
1,179,525/s 1.37 L.set(L.seq('x', 'y', 'z'), 1, undefined)
284,950/s 1.00 L.modify(values, x => x + x, bst)
443,036/s 1.00 L.collect(values, bst)
97,632/s 1.00 fromPairs(bstPairs)
56,276/s 1.00 L.get(L.slice(100, -100), xs10000)
40,472/s 1.39 R.slice(100, -100, xs10000)
5,911,415/s 1.00 L.get(L.slice(1, -1), xs)
5,544,989/s 1.07 R.slice(1, -1, xs)
3,188,865/s 1.00 L.get(L.slice(10, -10), xs100)
2,672,422/s 1.19 R.slice(10, -10, xs100)
9,386,623/s 1.00 L.get(L.defaults(1), 2)
8,851,162/s 1.06 L.get(L.defaults(1), undefined)
30,073,738/s 1.00 L.get(defaults1, undefined)
28,660,806/s 1.05 L.get(defaults1, 2)
10,012,353/s 1.00 L.get(L.define(1), 2)
9,817,035/s 1.02 L.get(L.define(1), undefined)
46,427,067/s 1.00 L.get(define1, undefined)
45,966,952/s 1.01 L.get(define1, 2)
15,312,111/s 1.00 L.get(L.valueOr(1), null)
15,106,079/s 1.01 L.get(L.valueOr(1), undefined)
14,284,098/s 1.07 L.get(L.valueOr(1), 2)
46,380,800/s 1.00 L.get(valueOr1, 2)
46,052,173/s 1.01 L.get(valueOr1, undefined)
45,749,521/s 1.01 L.get(valueOr1, null)
49,394/s 1.00 L.concatAs(toList, List, L.elems, xs100)
49,965/s 1.00 L.modify(L.flatten, inc, xsss100)
7,833,540/s 1.00 L.selectAs(x => x > 3 ? x : undefined, L.elems, pi)
4,448,086/s 1.76 R.find(x => x > 3, pi)
32,770/s 239.05 O.Fold.findOf(O.Traversal.traversed, x => x > 3, pi)
6,140,005/s 1.00 L.get(L.find(x => x !== 1, {hint: 0}), xs)
5,933,954/s 1.03 L.get(L.find(x => x !== 1), xs)
4,608,258/s 1.33 R.find(x => x !== 1, xs)
1,320,062/s 1.00 R.find(x => x !== 1, xs100)
902,106/s 1.46 L.get(L.find(x => x !== 1), xs100)
900,911/s 1.47 L.get(L.find(x => x !== 1, {hint: 0}), xs100)
186,687/s 1.00 R.find(x => x !== 1, xs1000)
109,054/s 1.71 L.get(L.find(x => x !== 1, {hint: 0}), xs1000)
108,286/s 1.72 L.get(L.find(x => x !== 1), xs1000)
4,331,759/s 1.00 L.get(valueOr0x0y, axay)
4,233,734/s 1.02 L.get(define0x0y, axay)
3,894,676/s 1.11 L.get(defaults0x0y, axay)
865,866/s 1.00 L.set(valueOr0x0y, 1, undefined)
856,274/s 1.01 L.set(define0x0y, 1, undefined)
770,947/s 1.12 L.set(defaults0x0y, 1, undefined)
1,150,943/s 1.00 L.set(L.findWith('x'), 2, axay)
6,793,006/s 1.00 L.get(aEb, {x: 1})
6,290,285/s 1.08 L.get(abS, {x: 1})
4,201,828/s 1.62 L.get(abM, {x: 1})
3,072,564/s 2.21 L.get(L.orElse('a', 'b'), {x: 1})
2,295,497/s 2.96 L.get(L.choices('a', 'b'), {x: 1})
4,075,886/s 1.00 L.get(abcS, {x: 1})
4,019,108/s 1.01 L.get(aEbEc, {x: 1})
3,267,810/s 1.25 L.get(abcM, {x: 1})
1,401,479/s 2.91 L.get(L.choices('a', 'b', 'c'), {x: 1})
1,122,000/s 3.63 L.get(L.choice('a', 'b', 'c'), {x: 1})
1,309,555/s 1.00 L.set(L.props('x', 'y'), {x: 2, y: 3}, {x: 1, y: 2, z: 4})
Various operations on partial lenses have been optimized for common cases, but there is definitely a lot of room for improvement. The goal is to make partial lenses fast enough that performance isn't the reason why you might not want to use them.
See bench.js for details.
As said in the first sentence of this document, lenses are convenient for performing updates on individual elements of immutable data structures. Having abilities such as nesting, adapting, recursing and restructuring using lenses makes the notion of an individual element quite flexible and, even further, traversals make it possible to selectively target zero or more elements of non-trivial data structures in a single operation. It can be tempting to try to do everything with lenses, but that will likely only lead to misery. It is important to understand that lenses are just one of many functional abstractions for working with data structures and sometimes other approaches can lead to simpler or easier solutions. Zippers, for example, are, in some ways, less principled and can implement queries and transforms that are outside the scope of lenses and traversals.
One type of use case which we've ran into multiple times and falls out of the sweet spot of lenses is performing uniform transforms over data structures. For example, we've run into the following use cases:
One approach to making such whole data structure spanning updates is to use a simple bottom-up transform. Here is a simple implementation for JSON based on ideas from the Uniplate library:
const descend = (w2w, w) => R.is(Object, w) ? R.map(w2w, w) : w
const substUp = (h2h, w) => descend(h2h, descend(w => substUp(h2h, w), w))
const transform = (w2w, w) => w2w(substUp(w2w, w))
transform(w2w, w) basically just performs a single-pass bottom-up transform
using the given function w2w over the given data structure w. Suppose we
are given the following data:
const sampleBloated = {
just: 'some',
extra: 'crap',
that: [
'we',
{want: 'to',
filter: ['out'],
including: {the: 'following',
extra: true,
fields: 1}}]
}
We can now remove the extra fields like this:
transform(R.ifElse(R.allPass([R.is(Object), R.complement(R.is(Array))]),
L.remove(L.props('extra', 'fields')),
R.identity),
sampleBloated)
// { just: 'some',
// that: [ 'we', { want: 'to',
// filter: ['out'],
// including: {the: 'following'} } ] }
Lenses are an old concept and there are dozens of academic papers on lenses and dozens of lens libraries for various languages. Below are just a few links—feel free to suggest more!
Contributions in the form of pull requests are welcome!
Before starting work on a major PR, it is a good idea to open an issue or maybe ask on gitter whether the contribution sounds like something that should be added to this library.
If you allow us to make changes to your PR, it can make the process smoother: Allowing changes to a pull request branch created from a fork. We also welcome starting the PR sooner, before it is ready to be merged, rather than later so we know what is going on and can help.
Aside from the code changes, a PR should also include tests, and documentation.
When implementing partial optics it is important to consider the behavior of the optics when the focus doesn't match the expectation of the optic and also whether the optic should propagate removal. Such behavior should also be tested.
It is best not to commit changes to generated files in PRs. Some of the files
in docs, and dist directories are generated.
The prepare script is the usual way to build after changes:
npm run prepare
It builds the dist and docs files and runs the lint rules and tests. You
can also run the scripts for those subtasks separately.
There is also a watch mode for development:
npm run watch
It starts watching the source files and runs dist and docs builds and tests after changes.
The tests in this library are written in a slightly atypical manner using thunks that are also used as the test descriptions. This way one doesn't need to invent names or write prose for tests.
There is also a special test that checks the arity of the exports. You'll notice it immediately if you add an export.
The test/types.js file contains contract or type predicates
for the library primitives. Those are also used when running tests to check
that the implementation matches the contracts. When you implement a new
combinator, you will also need to add a contract for the combinator.
When testing a partial optics, you should generally test both read and, usually
more importantly, write behaviour including attempts to read undefined or
unexpected data (both of these should be handled as undefined) and writing
undefined.
The docs folder contains the generated documentation. You can open the file
locally:
open docs/index.html
To actually build the docs (translate the markdown to html), you can run
npm run docs
or you can use the watch
npm run watch
which builds the docs if you save README.md. The watch also runs
LiveReload so if you have the plugin, your browser
will refresh automatically after changes.
FAQs
Partial lenses is a comprehensive, high-performance optics library for JavaScript
The npm package partial.lenses receives a total of 3,578 weekly downloads. As such, partial.lenses popularity was classified as popular.
We found that partial.lenses demonstrated a not healthy version release cadence and project activity because the last version was released a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Security News
Snyk's use of malicious npm packages for research raises ethical concerns, highlighting risks in public deployment, data exfiltration, and unauthorized testing.

Research
Security News
Socket researchers found several malicious npm packages typosquatting Chalk and Chokidar, targeting Node.js developers with kill switches and data theft.

Security News
pnpm 10 blocks lifecycle scripts by default to improve security, addressing supply chain attack risks but sparking debate over compatibility and workflow changes.