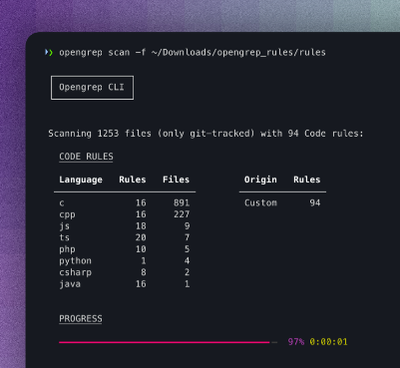
Security News
Opengrep Emerges as Open Source Alternative Amid Semgrep Licensing Controversy
Opengrep forks Semgrep to preserve open source SAST in response to controversial licensing changes.
partial.lenses
Advanced tools
[ Tutorial | Reference | Background ]
Lenses are primarily a convenient abstraction for performing updates on individual elements of immutable data structures. This library provides a collection of partial lenses. A partial lens can view optional data, insert new data, update existing data and remove existing data and can, for example, provide defaults and maintain required data structure parts.
In JavaScript, missing data can be mapped to undefined, which is what partial
lenses also do. When a part of a data structure is missing, an attempt to view
it returns undefined. When a part is missing, setting it to a defined value
inserts the new part. Setting an existing part to undefined removes it.
Partial lenses are defined in such a way that operations compose
and one can conveniently and robustly operate on deeply nested data structures.
Let's work with the following sample JSON object:
const data = { contents: [ { language: "en", text: "Title" },
{ language: "sv", text: "Rubrik" } ] }
First we import libraries
import * as L from "partial.lenses"
import R from "ramda"
and compose a parameterized lens for accessing texts:
const textIn = language =>
L.compose(L.prop("contents"),
L.required([]),
L.normalize(R.sortBy(R.prop("language"))),
L.find(R.whereEq({language})),
L.defaults({language}),
L.prop("text"),
L.defaults(""))
Take a moment to read through the above definition line by line. Each line has
a specific purpose. The purpose of the L.prop(...) lines is probably obvious.
The other lines we will mention below.
Thanks to the parameterized search part, L.find(R.whereEq({language})), of the
lens composition, we can use it to query texts:
L.get(textIn("sv"), data)
// "Rubrik"
L.get(textIn("en"), data)
// "Title"
Partial lenses can deal with missing data. If we use the partial lens to query a text that does not exist, we get the default:
L.get(textIn("fi"), data)
// ""
We get this default, rather than undefined, thanks to the last part,
L.defaults(""), of our lens composition. We get the default even if we query
from undefined:
L.get(textIn("fi"), undefined)
// ""
With partial lenses, undefined is the equivalent of empty or non-existent.
As with ordinary lenses, we can use the same lens to update texts:
L.set(textIn("en"), "The title", data)
// { contents: [ { language: "en", text: "The title" },
// { language: "sv", text: "Rubrik" } ] }
The same partial lens also allows us to insert new texts:
L.set(textIn("fi"), "Otsikko", data)
// { contents: [ { language: "en", text: "Title" },
// { language: "fi", text: "Otsikko" },
// { language: "sv", text: "Rubrik" } ] }
Note the position into which the new text was inserted. The array of texts is
kept sorted thanks to the L.normalize(R.sortBy(R.prop("language"))) part of
our lens.
Finally, we can use the same partial lens to remove texts:
L.set(textIn("sv"), undefined, data)
// { contents: [ { language: "en", text: "Title" } ] }
Note that a single text is actually a part of an object. The key to having the
whole object vanish, rather than just the text property, is the
L.defaults({language}) part of our lens composition. A L.defaults(value) lens
works symmetrically. When set with value, the result is undefined, which
means that the focus of the lens is to be removed.
If we remove all of the texts, we get the required value:
R.pipe(L.set(textIn("sv"), undefined),
L.set(textIn("en"), undefined))(data)
// { contents: [] }
The contents property is not removed thanks to the L.required([]) part of
our lens composition. L.required is the dual of L.defaults. L.defaults
replaces undefined values when viewed and L.required replaces undefined values
when set.
Note that unless defaults and required values are explicitly specified as part of the lens, they will both be undefined.
Take out one (or more) L.required(...), L.normalize(...) or L.defaults(...)
part(s) from the lens composition and try to predict what happens when you rerun
the examples with the modified lens composition. Verify your reasoning by
actually rerunning the examples.
For clarity, the previous code snippets avoided some of the shorthands that this library supports. In particular,
L.compose(...) can be abbreviated to use the default import, e.g. P(...),L.prop(string) can be abbreviated as string, andL.set(l, undefined, s) can be abbreviated as L.remove(l, s).It is also typical to compose lenses out of short paths following the schema of the JSON data being manipulated. Reconsider the lens from the start of the example:
const textIn = language =>
L.compose(L.prop("contents"),
L.required([]),
L.normalize(R.sortBy(R.prop("language"))),
L.find(R.whereEq({language})),
L.defaults({language}),
L.prop("text"),
L.defaults(""))
Following the structure or schema of the JSON, we could break this into three separate lenses:
Furthermore, we could organize the lenses into an object following the structure of the JSON:
const M = {
data: {
contents: P("contents",
L.required([]),
L.normalize(R.sortBy(R.prop("language"))))
},
contents: {
contentIn: language => P(L.find(R.whereEq({language})),
L.defaults({language}))
},
content: {
text: P("text", L.defaults(""))
}
}
Using the above object, we could rewrite the parameterized textIn lens as:
const textIn = language => P(M.data.contents,
M.contents.contentIn(language),
M.content.text)
This style of organizing lenses is overkill for our toy example. In a more
realistic case the data object would contain many more properties. Also,
rather than composing a lens, like textIn above, to access a leaf property
from the root of our object, we might actually compose lenses incrementally as
we inspect the model structure.
A case that we have run into multiple times is where we have an array of constant strings such as
const data = ["id-19", "id-76"]
that we wish to manipulate as if it was a collection of boolean flags. Here is a parameterized lens that does just that:
const flag = id =>
P(L.normalize(R.sortBy(R.identity)),
L.find(R.equals(id)),
L.replace(undefined, false),
L.replace(id, true))
Now we can treat individual constants as boolean flags:
L.get(flag("id-69"), data)
// false
L.get(flag("id-76"), data)
// true
In both directions:
L.set(flag("id-69"), true, data)
// ["id-19", "id-69", "id-76"]
L.set(flag("id-76"), false, data)
// ["id-19"]
The previous examples are based on actual use cases. In this section we look at a more involved example: BST, binary search tree, as a lens.
Binary search might initially seem to be outside the scope of definable lenses.
However, given basic BST operations, one could easily wrap them as a primitive
partial lens. But could we leverage lens combinators to build a BST lens more
directly? We can. The L.choose lens combinator allows for dynamic
construction of lenses based on examining the data structure being manipulated.
Inside L.choose we can write the ordinary BST logic to pick the correct branch
based on the key in the currently examined node and the key that we are looking
for. So, here is our first attempt at a BST lens:
const search = key =>
P(L.defaults({key}),
L.choose(n => key < n.key ? P("smaller", search(key)) :
n.key < key ? P("greater", search(key)) :
L.identity))
const valueOf = key => P(search(key), "value")
This actually works to a degree. We can use the valueOf lens constructor to
build a binary tree:
const t = R.reduce(
(tree, {key, value}) => L.set(valueOf(key), value, tree),
undefined,
[{key: "c", value: 1},
{key: "a", value: 2},
{key: "b", value: 3}])
t
// { smaller: { greater: { value: 3, key: 'b' }, value: 2, key: 'a' },
// value: 1,
// key: 'c' }
However, the above search lens constructor does not maintain the BST
structure when values are being removed:
L.remove(valueOf('c'), t)
// { smaller: { greater: { value: 3, key: 'b' },
// value: 2,
// key: 'a' },
// key: 'c' }
How do we fix this? We could check and transform the data structure to a BST
after changes. The L.normalize lens can be used for that purpose. Here is
the updated search definition:
const search = key =>
P(L.normalize(n =>
undefined !== n.value ? n :
n.smaller && !n.greater ? n.smaller :
!n.smaller && n.greater ? n.greater :
L.set(search(n.smaller.key), n.smaller, n.greater)),
L.defaults({key}),
L.choose(n => key < n.key ? P("smaller", search(key)) :
n.key < key ? P("greater", search(key)) :
L.identity))
Now we can also remove values from a binary tree:
L.remove(valueOf('c'), t)
// { greater: { value: 3, key: 'b' }, value: 2, key: 'a' }
As an exercise, you could improve the normalization to better maintain balance.
Perhaps you might even enhance it to maintain a balance condition such as
AVL or
Red-Black. Another
worthy exercise would be to make it so that the empty binary tree is null
rather than undefined.
Protip: The link headings for functions in this reference have naive approximate types as tooltips.
The lenses and operations on lenses are accessed via the default import:
import P, * as L from "partial.lenses"
Use of the default import, P, is optional and is an alias for L.compose.
In alphabetical order.
L.get(l, s)L.get(l, s) returns the focused element from a data structure.
For example:
L.get("y", {x: 112, y: 101})
// 101
L.modify(l, x2x, s)L.modify(l, x2x, s) allows one to map over the focused element of a data
structure.
For example:
L.modify("elems", R.map(L.remove("x")), {elems: [{x: 1, y: 2}, {x: 3, y: 4}]})
// {elems: [{y: 2}, {y: 4}]}
L.remove(l, s)L.remove(l, s) is equivalent to L.set(l, undefined, s). With partial
lenses, setting to undefined typically has the effect of removing the focused
element.
For example:
L.remove(P("a", "b"), {a: {b: 1}, x: {y: 2}})
// {x: {y: 2}}
L.removeAll(l, s)L.removeAll(l, s) removes all the non undefined items targeted by the lens
l from s. This only makes sense for a lens that
undefined when it doesn't find an item to focus on.For example:
L.removeAll(L.findWith("a"), [{x: 1}, {a: 2}, {a: 3, y: 4}, {z: 5}])
// [{x: 1}, {y: 4}, {z: 5}]
L.set(l, x, s)L.set(l, x, s) is equivalent to L.modify(l, () => x, s).
For example:
L.set(P("a", 0, "x"), 11, {id: "z"})
// {a: [{x: 11}], id: "z"}
In alphabetical order.
L.appendL.append is a special semi-degenerate lens that operates on arrays. The view
of L.append is always undefined. Setting L.append to undefined has no
effect by itself. Setting L.append to a defined value appends the value to
the end of the focused array.
For example:
L.set(L.append, "x", undefined)
// [ 'x' ]
L.augment({prop: obj => val, ...props})L.augment({prop: obj => val, ...props}) is given a template of functions to
compute new properties. When viewing or setting undefined, the result is
undefined. When viewing a defined object, the object is extended with the
computed properties. When set with a defined object, the extended properties
are removed.
For example:
L.modify(L.augment({y: r => r.x + 1}), r => ({x: r.x + r.y, y: 2, z: r.x - r.y}), {x: 1})
// { x: 3, z: -1 }
L.chain(a2bPLens, aPLens)L.chain(a2bPLens, aPLens) is equivalent to
L.compose(aPLens, L.choose(aMaybe =>
aMaybe === undefined
? L.nothing
: a2bPLens(aMaybe)))
With the just, chain, choice and nothing combinators, one can view
partial lenses as subsuming the maybe monad. Of course, the whole point of
lenses is that they are bidirectional and the special lenses just and
nothing are essentially degenerate.
L.choose(maybeValue => PLens)L.choose(maybeValue => PLens) creates a lens whose operation is determined by
the given function that maps the underlying view, which can be undefined, to a
lens. In other words, the L.choose combinator allows a lens to be constructed
after examining the data structure being manipulated.
For example, given:
const majorAxis = L.choose(({x, y} = {}) =>
Math.abs(x) < Math.abs(y) ? "y" : "x")
we get:
L.get(majorAxis, {x: 1, y: 2})
// 2
L.get(majorAxis, {x: -3, y: 1})
// -3
L.modify(majorAxis, R.negate, {x: 2, y: -3})
// { y: 3, x: 2 }
L.choice(...ls)L.choice(...ls) returns a partial lens that acts like the first of the given
lenses, ls, whose view is not undefined on the given target. When the views
of all of the given lenses are undefined, the returned lens acts like
L.nothing, which is the identity element of L.choice.
L.compose(...ls)The default import P and L.compose refer to the one and same function, which
performs lens composition. The following equations characterize lens
composition:
L.compose() = L.identity
L.compose(l) = l
L.get(L.compose(l, ...ls)) = R.pipe(L.get(l), ...ls.map(L.get))
L.modify(L.compose(l, ...ls)) = R.pipe(L.modify(l), ...ls.map(L.modify))
For example:
L.get(P("a", 1), {a: ["b", "c"]})
// "c"
L.defaults(out)L.defaults(out) is the same as L.replace(undefined, out). L.defaults is
used to specify a default value for an element in case it is missing. This can
be useful to avoid having to check for and provide default behavior elsewhere.
For example:
L.get(P("items", L.defaults([])), {})
// []
L.get(P("items", L.defaults([])), {items: [1, 2, 3]})
// [ 1, 2, 3 ]
L.define(value)L.define(value) is the same as P(L.required(value), L.defaults(value)).
L.define is used to specify a value to act as both the default value and the
required value for an element.
L.filter(predicate)L.filter(predicate) operates on arrays. When viewed, only elements matching
the given predicate will be returned. When set, the resulting array will be
formed by concatenating the set array and the complement of the filtered
context. If the resulting array would be empty, the whole result will be
undefined.
For example:
L.remove(L.filter(x => x <= 2), [3,1,4,1,5,9,2])
// [ 3, 4, 5, 9 ]
Note: An alternative design for filter could implement a smarter algorithm to
combine arrays when set. For example, an algorithm based on
edit distance could be used to
maintain relative order of elements. While this would not be difficult to
implement, it doesn't seem to make sense, because in most cases use of
normalize would be preferable.
L.find(predicate)L.find(predicate) operates on arrays like L.index, but the index to be
viewed is determined by finding the first element from the input array that
matches the given predicate. When no matching element is found the effect is
same as with L.append.
L.removeAll(L.find(x => x <= 2), [3,1,4,1,5,9,2])
// [ 3, 4, 5, 9 ]
L.findWith(...ls)L.findWith(...ls) chooses an index from an array through which the given lens,
P(...ls), focuses on a defined item and then returns a lens that focuses on
that item.
For example:
L.get(L.findWith("x"), [{z: 6}, {x: 9}, {y: 6}])
// 9
L.set(L.findWith("x"), 3, [{z: 6}, {x: 9}, {y: 6}])
// [ { z: 6 }, { x: 3 }, { y: 6 } ]
L.identityL.identity is the identity element of lens composition. The following
equations characterize L.identity:
L.get(L.identity, x) = x
L.modify(L.identity, f, x) = f(x)
L.compose(L.identity, l) = l
L.compose(l, L.identity) = l
L.index(integer)L.index(integer) or integer focuses on the specified array index.
NOTE: There is a gotcha related to removing elements from an array. Namely,
when the last element is removed, the result is undefined rather than an empty
array. This is by design, because this allows the removal to propagate upwards.
It is not uncommon, however, to have cases where removing the last element from
an array must not remove the array itself. In such cases you want to use
L.required([]) to access the array. Consider the following examples without
L.required([]):
L.remove(0, ["a", "b"])
// [ 'b' ]
L.remove(0, ["b"])
// undefined
L.remove(P("elems", 0), {elems: ["b"], some: "thing"})
// { some: 'thing' }
Then consider the same examples with L.required([]):
L.remove(P(L.required([]), 0), ["a", "b"])
// [ 'b' ]
L.remove(P(L.required([]), 0), ["b"])
// []
L.remove(P("elems", L.required([]), 0), {elems: ["b"], some: "thing"})
// { elems: [], some: 'thing' }
L.just(value)L.just(x) is equivalent to L.compose(L.nothing, L.defaults(x)) and is a
special degenerate lens whose view is always x and writing through the lens
has no effect. In other words, for all x, y and z:
L.get(L.just(z), x) = z
L.set(L.just(z), y, x) = x
L.just can be seen as the unit function of the monad formed with L.chain.
L.lens(get, set)L.lens(get, set) creates a new primitive lens. One should think twice before
introducing a new primitive lens—most of the combinators in this library
have been introduced to reduce the need to write new primitive lenses. With
that said, there are still valid reasons to create new primitive lenses. For
example, here is a lens that we've used in production, written with the help of
Moment.js, to bidirectionally convert a pair of start
and end times to a duration:
const timesAsDuration = L.lens(
({start, end} = {}) => {
if (undefined === start)
return undefined
if (undefined === end)
return "Infinity"
return moment.duration(moment(end).diff(moment(start))).toJSON()
},
(duration, {start = moment().toJSON()} = {}) => {
if (undefined === duration || "Infinity" === duration) {
return {start}
} else {
return {
start,
end: moment(start).add(moment.duration(duration)).toJSON()
};
}
}
)
When composed with L.pick, to flexibly pick the start and end times, the
above can be adapted to work in a wide variety of cases. However, the above
lens will never be added to this library, because it would require adding
dependency to Moment.js.
L.normalize(value => value)L.normalize(value => value) maps the value with same given transform when
viewed and set and implicitly maps undefined to undefined. More specifically,
L.normalize(transform) is equivalent to R.lens(toPartial(transform), toPartial(transform)) where
const toPartial = transform => x => undefined === x ? x : transform(x)
The main use case for normalize is to make it easy to determine whether, after
a change, the data has actually changed. By keeping the data normalized, a
simple R.equals comparison will do.
L.nothingL.nothing is a special degenerate lens whose view is always undefined and
setting through L.nothing has no effect. In other words, for all x and y:
L.get(L.nothing, x) = undefined
L.set(L.nothing, y, x) = x
L.nothing is the identity element of L.choice.
L.orElse(backup, primary)L.orElse(backup, primary) acts like primary when its view is not undefined
and otherwise like backup. You can use L.orElse on its own with
R.reduceRight (and R.reduce) to create an associative choice over lenses or
use L.orElse to specify a default or backup lens for L.choice, for example.
L.pick({p1: l1, ...pls})L.pick({p1: l1, ...pls}) creates a lens out of the given object template of
lenses and allows one to pick apart a data structure and then put it back
together. When viewed, an object is created, whose properties are obtained by
viewing through the lenses of the template. When set with an object, the
properties of the object are set to the context via the lenses of the template.
undefined is treated as the equivalent of empty or non-existent in both
directions.
For example, let's say we need to deal with data and schema in need of some semantic restructuring:
const data = {px: 1, py: 2, vx: 1.0, vy: 0.0}
We can use L.pick to create lenses to pick apart the data and put it back
together into a more meaningful structure:
const asVec = prefix => L.pick({x: prefix + "x", y: prefix + "y"})
const sanitize = L.pick({pos: asVec("p"), vel: asVec("v")})
We now have a better structured view of the data:
L.get(sanitize, data)
// { pos: { x: 1, y: 2 }, vel: { x: 1, y: 0 } }
That works in both directions:
L.modify(P(sanitize, "pos", "x"), R.add(5), data)
// { px: 6, py: 2, vx: 1, vy: 0 }
NOTE: In order for a lens created with L.pick to work in a predictable
manner, the given lenses must operate on independent parts of the data
structure. As a trivial example, in L.pick({x: "same", y: "same"}) both of
the resulting object properties, x and y, address the same property of the
underlying object, so writing through the lens will give unpredictable results.
Note that, when set, L.pick simply ignores any properties that the given
template doesn't mention. Also note that the underlying data structure need not
be an object.
L.prop(string)L.prop(string) or string focuses on the specified object property.
L.props(...strings)L.props(k1, ..., kN) is equivalent to L.pick({[k1]: k1, ..., [kN]: kN}) and
focuses on a subset of properties of an object, allowing one to treat the subset
of properties as a unit. The view of L.props is undefined when none of the
properties is defined. Otherwise the view is an object containing a subset of
the properties. Setting through L.props updates the whole subset of
properties, which means that any undefined properties are removed if they did
exists previously. When set, any extra properties are ignored.
L.set(L.props("x", "y"), {x: 4}, {x: 1, y: 2, z: 3})
// { z: 3, x: 4 }
L.replace(inn, out)L.replace(inn, out), when viewed, replaces the value inn with out and vice
versa when set. Values are compared using R.equals (see
equals).
For example:
L.get(L.replace(1, 2), 1)
// 2
L.set(L.replace(1, 2), 2, 0)
// 1
The main use case for replace is to handle optional and required properties
and elements. In most cases, rather than using replace, you will make
selective use of defaults and required.
L.required(inn)L.required(inn) is the same as L.replace(inn, undefined). L.required is
used to specify that an element is not to be removed; in case it is removed, the
given value will be substituted instead.
For example:
L.remove(P("items", 0), {items: [1]})
// undefined
L.remove(P(L.required({}), "items", 0), {items: [1]})
// {}
L.remove(P("items", L.required([]), 0), {items: [1]})
// { items: [] }
Conversions between lens libraries.
L.fromRamda(lens)L.fromRamda(lens) converts the given Ramda lens to a partial lens. Note that
this does not change the behavior of the lens on undefined values.
L.toRamda(plens)L.toRamda(plens) converts the given partial lens to a Ramda lens. Note that
this does not change the behavior of the lens on undefined values.
L.log(...labels)L.log(...labels) is an identity lens that outputs console.log messages with
the given labels (or format in Node.js) when data flows in either direction,
get or set, through the lens.
For example:
L.get(P("x", L.log()), {x: 10})
// get 10
// 10
L.set(P("x", L.log("x")), "11", {x: 10})
// x get 10
// x set 11
// { x: '11' }
L.set(P("x", L.log("%s x: %j")), "11", {x: 10})
// get x: 10
// set x: "11"
// { x: '11' }
Consider the following REPL session using Ramda 0.19.1:
R.set(R.lensPath(["x", "y"]), 1, {})
// { x: { y: 1 } }
R.set(R.compose(R.lensProp("x"), R.lensProp("y")), 1, {})
// TypeError: Cannot read property 'y' of undefined
R.view(R.lensPath(["x", "y"]), {})
// undefined
R.view(R.compose(R.lensProp("x"), R.lensProp("y")), {})
// TypeError: Cannot read property 'y' of undefined
R.set(R.lensPath(["x", "y"]), undefined, {x: {y: 1}})
// { x: { y: undefined } }
R.set(R.compose(R.lensProp("x"), R.lensProp("y")), undefined, {x: {y: 1}})
// { x: { y: undefined } }
One might assume that R.lensPath([p0, ...ps]) is equivalent to
R.compose(R.lensProp(p0), ...ps.map(R.lensProp)), but that is not the case.
With partial lenses you can robustly compose a path lens from prop lenses
L.compose(L.prop(p0), ...ps.map(L.prop)) or just use the shorthand notation
P(p0, ...ps).
To illustrate the idea we could give lenses the naive type definition
type Lens s a = (s -> a, a -> s -> s)
defining a lens as a pair of a getter and a setter. The type of a partial lens would then be
type PLens s a = (Maybe s -> Maybe a, Maybe a -> Maybe s -> Maybe s)
which we can simplify to
type PLens s a = Lens (Maybe s) (Maybe a)
This means that partial lenses can be composed, viewed, mapped over and set using the same operations as with ordinary lenses. However, primitive partial lenses (e.g. L.prop) are not necessarily the same as primitive ordinary lenses (e.g. Ramda's lensProp).
FAQs
Partial lenses is a comprehensive, high-performance optics library for JavaScript
The npm package partial.lenses receives a total of 4,840 weekly downloads. As such, partial.lenses popularity was classified as popular.
We found that partial.lenses demonstrated a not healthy version release cadence and project activity because the last version was released a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Security News
Opengrep forks Semgrep to preserve open source SAST in response to controversial licensing changes.

Security News
Critics call the Node.js EOL CVE a misuse of the system, sparking debate over CVE standards and the growing noise in vulnerability databases.

Security News
cURL and Go security teams are publicly rejecting CVSS as flawed for assessing vulnerabilities and are calling for more accurate, context-aware approaches.