.. |wheels| image:: https://github.com/giotto-ai/giotto-ph/actions/workflows/wheels.yml/badge.svg .. _wheels:
.. |ci| image:: https://github.com/giotto-ai/giotto-ph/actions/workflows/ci.yml/badge.svg .. _ci:
.. |docs| image:: https://github.com/giotto-ai/giotto-ph/actions/workflows/deploy-github-pages.yml/badge.svg .. _docs:
|wheels|_ |ci|_ |docs|_
giotto-ph is a high-performance implementation of Vietoris–Rips (VR) persistence on the CPU, and is distributed under the GNU AGPLv3 license.
It consists of an improved reimplementation of Morozov and Nigmetov's "lock-free Ripser" <https://dl.acm.org/doi/10.1145/3350755.3400244>_
and in addition makes use of a parallel implementation of the apparent pairs optimization used in Ripser v1.2 <https://github.com/Ripser/ripser>.
It also contains an improved reimplementation of GUDHI's Edge Collapse (EC) algorithm <https://hal.inria.fr/hal-02395227> and offers support
for weighted VR filtrations. See also Morozov's Ripser fork <https://github.com/mrzv/ripser/tree/lockfree>, Nigmetov's
Oineus library <https://github.com/grey-narn/oineus>, and GUDHI's EC implementation <http://gudhi.gforge.inria.fr/doc/latest/group__edge__collapse.html>_.
giotto-ph is part of the Giotto <https://github.com/giotto-ai>_ family of open-source projects and designed for tight integration with
the giotto-tda <https://github.com/giotto-ai/giotto-tda>_ and pyflagser <https://github.com/giotto-ai/giotto-tda>_ libraries.
giotto-ph is the result of a collaborative effort between L2F SA <https://www.l2f.ch/>,
the Laboratory for Topology and Neuroscience <https://www.epfl.ch/labs/hessbellwald-lab/> at EPFL,
and the Institute of Reconfigurable & Embedded Digital Systems (REDS) <https://heig-vd.ch/en/research/reds>_ of HEIG-VD.
.. _L2F team: business@l2f.ch
giotto-ph is distributed under the AGPLv3 license <https://github.com/giotto-ai/giotto-tda/blob/master/LICENSE>.
If you need a different distribution license, please contact the L2F team.
Computing persistence barcodes of large datasets and in high homology degrees is challenging even on modern hardware. giotto-ph's persistent homology backend
is able to distribute the key stages of the computation (namely, search for apparent pairs and coboundary matrix reduction) across an arbitrary number of available CPU threads.
On challenging datasets, the scaling is quite favourable as shown in the following figure (for more details, see our paper linked below):
.. image:: https://raw.githubusercontent.com/giotto-ai/giotto-ph/main/docs/images/multithreading_speedup.svg :width: 500px :align: center
Basic imports:
.. code-block:: python
import numpy as np
from gph import ripser_parallel
Persistence diagram of a random point cloud of 100 points in 3D Euclidean space, up to homology dimension 2, using all available threads:
.. code-block:: python
pc = np.random.random((100, 3))
dgm = ripser_parallel(pc, maxdim=2, n_threads=-1)
You can also work with distance matrices by passing metric="precomputed":
.. code-block:: python
from scipy.spatial.distance import pdist, squareform
# A distance matrix
dm = squareform(pdist(pc))
dgm = ripser_parallel(pc, metric="precomputed", maxdim=2, n_threads=-1)
More generally, you can work with dense or sparse adjacency matrices of weighted graphs. Here is a dense square matrix interpreted as the adjacency matrix of a fully connected weighted graph with 100 vertices:
.. code-block:: python
# Entries can be negative. The only constraint is that, for every i and j, dm[i, j] ≥ max(dm[i, i], dm[j, j])
# With dense input, the lower diagonal is ignored
adj_dense = np.random.random((100, 100))
np.fill_diagonal(adj_dense, 0)
dgm = ripser_parallel(adj_dense, metric="precomputed", maxdim=2, n_threads=-1)
And here is a sparse adjacency matrix:
.. code-block:: python
# See API reference for treatment of entries below the diagonal
from scipy.sparse import random
adj_sparse = random(100, 100, density=0.1)
dgm = ripser_parallel(adj_sparse, metric="precomputed", maxdim=2, n_threads=-1)
Push the computation to higher homology dimensions and larger point clouds/distance matrices/adjacency matrices using edge collapses:
.. code-block:: python
dgm_higher = ripser_parallel(pc, maxdim=5, collapse_edges=True, n_threads=-1)
(Note: not all datasets and configurations will benefit from edge collapses. For more details, see our paper below.)
Use the weights and weight_params parameters to constructed a weighted Rips filtration as defined in this paper <https://doi.org/10.1007/978-3-030-43408-3_2>_. weights can either be a custom 1D array of vertex weights, or the string "DTM" for distance-to-measure reweighting:
.. code-block:: python
dgm_dtm = ripser_parallel(pc, weights="DTM", n_threads=-1)
Jupyter notebook tutorials can be found in the examples folder <https://github.com/giotto-ai/giotto-ph/blob/main/examples>_.
The API reference can be found at https://giotto-ai.github.io/giotto-ph.
The latest stable version of giotto-ph requires:
The simplest way to install giotto-ph is using pip ::
python -m pip install -U giotto-ph
If necessary, this will also automatically install all the above dependencies. Note: we recommend
upgrading pip to a recent version as the above may fail on very old versions.
Please consult the dedicated page <https://giotto-ai.github.io/giotto-ph/build/html/installation.html#developer-installation>_
for detailed instructions on how to build giotto-ph from sources across different platforms.
.. _contributing-section:
We welcome new contributors of all experience levels. The Giotto community goals are to be helpful, welcoming,
and effective. To learn more about making a contribution to giotto-ph, please consult the relevant page <https://giotto-ai.github.io/gtda-docs/latest/contributing/index.html>_.
After installation, you can launch the test suite from inside the source directory ::
pytest gph
If you use giotto-ph in a scientific publication, we would appreciate citations to the following paper:
giotto-ph: A Python Library for High-Performance Computation of Persistent Homology of Vietoris–Rips Filtrations <https://arxiv.org/abs/2107.05412>_, Burella Pérez et al, arXiv:2107.05412, 2021.
You can use the following BibTeX entry:
.. code:: bibtex
@misc{burella2021giottoph,
title={giotto-ph: A Python Library for High-Performance Computation of Persistent Homology of Vietoris--Rips Filtrations},
author={Julián Burella Pérez and Sydney Hauke and Umberto Lupo and Matteo Caorsi and Alberto Dassatti},
year={2021},
eprint={2107.05412},
archivePrefix={arXiv},
primaryClass={cs.CG}
}
giotto-ai Slack workspace: https://slack.giotto.ai/
FAQs
High performance tool for Persistent Homology computations.
We found that giotto-ph demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?
Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.
Security News
Research
The Socket Research Team breaks down a malicious wrapper package that uses obfuscation to harvest credentials and exfiltrate sensitive data.
Research
Security News
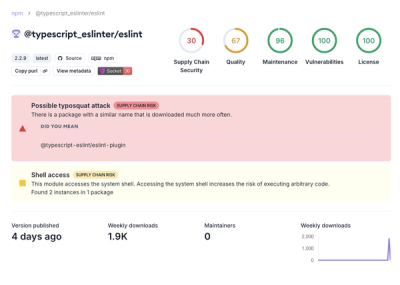
Attackers used a malicious npm package typosquatting a popular ESLint plugin to steal sensitive data, execute commands, and exploit developer systems.
Security News
The Ultralytics' PyPI Package was compromised four times in one weekend through GitHub Actions cache poisoning and failure to rotate previously compromised API tokens.