Product
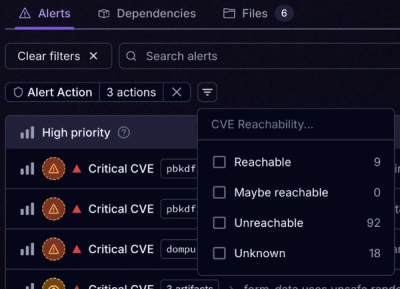
Introducing Tier 1 Reachability: Precision CVE Triage for Enterprise Teams
Socket’s new Tier 1 Reachability filters out up to 80% of irrelevant CVEs, so security teams can focus on the vulnerabilities that matter.
ml_dtypes is a stand-alone implementation of several NumPy dtype extensions used in machine learning.
ml_dtypes is a stand-alone implementation of several NumPy dtype extensions used in machine learning libraries, including:
bfloat16:
an alternative to the standard float16 formatfloat8_e3m4float8_e4m3float8_e4m3b11fnuzfloat8_e4m3fnfloat8_e4m3fnuzfloat8_e5m2float8_e5m2fnuzfloat8_e8m0fnufloat4_e2m1fnfloat6_e2m3fnfloat6_e3m2fnint2int4uint2uint4See below for specifications of these number formats.
The ml_dtypes package is tested with Python versions 3.9-3.12, and can be installed
with the following command:
pip install ml_dtypes
To test your installation, you can run the following:
pip install absl-py pytest
pytest --pyargs ml_dtypes
To build from source, clone the repository and run:
git submodule init
git submodule update
pip install .
>>> from ml_dtypes import bfloat16
>>> import numpy as np
>>> np.zeros(4, dtype=bfloat16)
array([0, 0, 0, 0], dtype=bfloat16)
Importing ml_dtypes also registers the data types with numpy, so that they may
be referred to by their string name:
>>> np.dtype('bfloat16')
dtype(bfloat16)
>>> np.dtype('float8_e5m2')
dtype(float8_e5m2)
bfloat16A bfloat16 number is a single-precision float truncated at 16 bits.
Exponent: 8, Mantissa: 7, exponent bias: 127. IEEE 754, with NaN and inf.
float4_e2m1fnExponent: 2, Mantissa: 1, bias: 1.
Extended range: no inf, no NaN.
Microscaling format, 4 bits (encoding: 0bSEEM) using byte storage (higher 4
bits are unused). NaN representation is undefined.
Possible absolute values: [0, 0.5, 1, 1.5, 2, 3, 4, 6]
float6_e2m3fnExponent: 2, Mantissa: 3, bias: 1.
Extended range: no inf, no NaN.
Microscaling format, 6 bits (encoding: 0bSEEMMM) using byte storage (higher 2
bits are unused). NaN representation is undefined.
Possible values range: [-7.5; 7.5]
float6_e3m2fnExponent: 3, Mantissa: 2, bias: 3.
Extended range: no inf, no NaN.
Microscaling format, 4 bits (encoding: 0bSEEEMM) using byte storage (higher 2
bits are unused). NaN representation is undefined.
Possible values range: [-28; 28]
float8_e3m4Exponent: 3, Mantissa: 4, bias: 3. IEEE 754, with NaN and inf.
float8_e4m3Exponent: 4, Mantissa: 3, bias: 7. IEEE 754, with NaN and inf.
float8_e4m3b11fnuzExponent: 4, Mantissa: 3, bias: 11.
Extended range: no inf, NaN represented by 0b1000'0000.
float8_e4m3fnExponent: 4, Mantissa: 3, bias: 7.
Extended range: no inf, NaN represented by 0bS111'1111.
The fn suffix is for consistency with the corresponding LLVM/MLIR type, signaling this type is not consistent with IEEE-754. The f indicates it is finite values only. The n indicates it includes NaNs, but only at the outer range.
float8_e4m3fnuz8-bit floating point with 3 bit mantissa.
An 8-bit floating point type with 1 sign bit, 4 bits exponent and 3 bits mantissa. The suffix fnuz is consistent with LLVM/MLIR naming and is derived from the differences to IEEE floating point conventions. F is for "finite" (no infinities), N for with special NaN encoding, UZ for unsigned zero.
This type has the following characteristics:
0bSEEEEMMM0b10000000float8_e5m2Exponent: 5, Mantissa: 2, bias: 15. IEEE 754, with NaN and inf.
float8_e5m2fnuz8-bit floating point with 2 bit mantissa.
An 8-bit floating point type with 1 sign bit, 5 bits exponent and 2 bits mantissa. The suffix fnuz is consistent with LLVM/MLIR naming and is derived from the differences to IEEE floating point conventions. F is for "finite" (no infinities), N for with special NaN encoding, UZ for unsigned zero.
This type has the following characteristics:
0bSEEEEEMM0b10000000float8_e8m0fnuOpenCompute MX scale format E8M0, which has the following properties:
int2, int4, uint2 and uint42 and 4-bit integer types, where each element is represented unpacked (i.e., padded up to a byte in memory).
NumPy does not support types smaller than a single byte: for example, the
distance between adjacent elements in an array (.strides) is expressed as
an integer number of bytes. Relaxing this restriction would be a considerable
engineering project. These types therefore use an unpacked representation, where
each element of the array is padded up to a byte in memory. The lower two or four
bits of each byte contain the representation of the number, whereas the remaining
upper bits are ignored.
If you're exploring the use of low-precision dtypes in your code, you should be
careful to anticipate when the precision loss might lead to surprising results.
One example is the behavior of aggregations like sum; consider this bfloat16
summation in NumPy (run with version 1.24.2):
>>> from ml_dtypes import bfloat16
>>> import numpy as np
>>> rng = np.random.default_rng(seed=0)
>>> vals = rng.uniform(size=10000).astype(bfloat16)
>>> vals.sum()
256
The true sum should be close to 5000, but numpy returns exactly 256: this is
because bfloat16 does not have the precision to increment 256 by values less than
1:
>>> bfloat16(256) + bfloat16(1)
256
After 256, the next representable value in bfloat16 is 258:
>>> np.nextafter(bfloat16(256), bfloat16(np.inf))
258
For better results you can specify that the accumulation should happen in a
higher-precision type like float32:
>>> vals.sum(dtype='float32').astype(bfloat16)
4992
In contrast to NumPy, projects like JAX which support low-precision arithmetic more natively will often do these kinds of higher-precision accumulations automatically:
>>> import jax.numpy as jnp
>>> jnp.array(vals).sum()
Array(4992, dtype=bfloat16)
This is not an officially supported Google product.
The ml_dtypes source code is licensed under the Apache 2.0 license
(see LICENSE). Pre-compiled wheels are built with the
EIGEN project, which is released under the
MPL 2.0 license (see LICENSE.eigen).
FAQs
ml_dtypes is a stand-alone implementation of several NumPy dtype extensions used in machine learning.
We found that ml-dtypes demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 2 open source maintainers collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Product
Socket’s new Tier 1 Reachability filters out up to 80% of irrelevant CVEs, so security teams can focus on the vulnerabilities that matter.
Research
/Security News
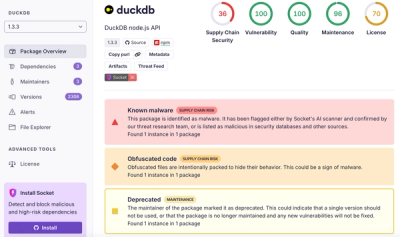
Ongoing npm supply chain attack spreads to DuckDB: multiple packages compromised with the same wallet-drainer malware.

Security News
The MCP Steering Committee has launched the official MCP Registry in preview, a central hub for discovering and publishing MCP servers.