slidingpuzzle

Sliding Puzzle

Installation | Documentation (Latest | Stable)

A package for solving sliding tile puzzles.

• Sliding Puzzle
  • Installation
  • Simple Example
  • Working with Boards
  • Solving Boards
  • Algorithms
  • Heuristics
    • Neural Nets
    • Datasets
    • Train
  • Custom Models
  • Contributing

Installation

pip install slidingpuzzle

Simple Example

from slidingpuzzle import *

board = from_rows([8,3,1], [4,0,2], [5,6,7])
solution = search(board)

print_board(board)
print(solution)

8 3 1
4   2
5 6 7
solution=[3, 1, 2, 3, 6, 5, 4, 8, 1, 2, 3, 6, 5, 7, 6, 5, 8, 4, 7, 8, 5, 6]
solution_len=22, generated=1059, expanded=618, unvisited=442, visited=394

Working with Boards

>>> from slidingpuzzle import *
>>> board = new_board(3, 3)
>>> print_board(board)
1 2 3
4 5 6
7 8
>>> print_board(shuffle(board))
3 5 7
  2 1
6 8 4

Using any of the provided shuffle() methods will guarantee a solvable board. The board is modified in-place and returned for chaining convenience.

Boards are stored as numpy arrays. The number 0 is reserved for the blank.

>>> board
array([[3, 5, 7],
       [0, 2, 1],
       [6, 8, 4]])

You can easily build your own boards using numpy or any of the provided convenience methods:

>>> board = from_rows([1, 2, 3], [4, 5, 6], [7, 8, 0])
>>> print_board(board)
1 2 3
4 5 6
7 8
>>> board = from_cols([1, 2, 3], [4, 5, 6], [7, 8, 0])
>>> print_board(board)
1 4 7
2 5 8
3 6
>>> board = from_iter(3, 3, [1, 2, 3, 4, 5, 6, 7, 8, 0])
>>> print_board(board)
1 2 3
4 5 6
7 8
>>> board = from_iter(3, 3, [1, 2, 3, 4, 5, 6, 7, 8, 0], row_major=False)
>>> print_board(board)
1 4 7
2 5 8
3 6
>>> flatten_board(board)
[1, 4, 7, 2, 5, 8, 3, 6, 0]
>>> freeze_board(board)
((1, 4, 7), (2, 5, 8), (3, 6, 0))

Not all board configurations are solvable.

>>> is_solvable(board)
False

The search() routine will validate the provided board before beginning, and may throw a ValueError if the board is illegal.

>>> board = shuffle(new_board(3, 3))
>>> board
array([[7, 5, 4],
       [3, 0, 1],
       [8, 6, 2]])
>>> find_blank(board)
(1, 1)
>>> find_tile(board, 3)
(1, 0)

Note: Coordinates are in (row, column) order.

Provided a board size, you can find the target position for a particular tile. For example, to locate the destination of the 6 tile on a 3x3 board:

>>> get_goal_yx(3, 3, 6)
(1, 2)

Moves are represented as coordinates adjacent to the blank.

>>> board
array([[7, 5, 4],
       [3, 0, 1],
       [8, 6, 2]])
>>> moves = get_next_moves(board)
>>> moves
[(1, 0), (1, 2), (0, 1), (2, 1)]
>>> swap_tiles(board, moves[0])
array([[7, 5, 4],
       [0, 3, 1],
       [8, 6, 2]])

Notice that if only one tile coordinate is provided to swap_tiles() the blank location is located automatically and used.

You can also use a tile number and it will be located automatically.

>>> swap_tiles(board, 7, 5)
array([[5, 7, 4],
       [0, 3, 1],
       [8, 6, 2]])

Solving Boards

The default search is A* with linear_conflict_distance() as the heuristic:

>>> board = shuffle(new_board(3, 3))
>>> print_board(board)
5 7 6
4   2
1 8 3
>>> search(board)
solution=[7, 6, 2, 3, 8, 7, 6, 2, 3, 6, 4, 1, 7, 8, 6, 3, 2, 5, 1, 4, 5, 2, 3, 6]
solution_len=24, generated=2796, expanded=1662, unvisited=1135, visited=1045

• generated is the total number of nodes generated during the search
• expanded is the total number of nodes that were evaluated (removed from search frontier)
• unvisited is the number of nodes that we never reached because search terminated early (search frontier, "open")
• visited is the number of unique states visited (expanded minus duplicate state expansions, "closed")

>>> search(board, heuristic=manhattan_distance)
solution=[7, 6, 2, 3, 8, 7, 4, 5, 6, 4, 5, 1, 7, 5, 4, 6, 1, 4, 6, 2, 3, 6, 5, 8]
solution_len=24, generated=8614, expanded=5604, unvisited=3011, visited=3225

A weaker heuristic takes longer, but finds an optimal solution. Note that the solution is slightly different (there may be many equally good solutions).

>>> search(board, "bfs")
solution=[4, 1, 8, 4, 7, 5, 1, 7, 4, 8, 7, 4, 5, 6, 2, 3, 8, 5, 6, 2, 3, 6, 5, 8]
solution_len=24, generated=363472, expanded=305020, unvisited=58453, visited=135180

BFS is guaranteed to find the optimal solution, but it can take a very long time.

>>> search(board, "greedy")
solution=[7, 6, 2, 3, 8, 7, 4, 1, 7, 4, 6, 2, 3, 6, 4, 8, 6, 3, 2, 5, 1, 4, 5, 2, 3, 6]
solution_len=26, generated=109, expanded=52, unvisited=58, visited=39

Greedy search finds a solution quickly, but the solution is of lower quality.

>>> search(board, weight=4)
solution=[7, 6, 2, 3, 8, 7, 4, 1, 7, 4, 6, 2, 3, 6, 4, 8, 6, 3, 2, 5, 1, 4, 5, 2, 3, 6]
solution_len=26, generated=125, expanded=68, unvisited=58, visited=45

Here we use Weighted A* to find a bounded suboptimal solution. In this case, we know that the solution found will be no larger than 4x the length of the optimal solution.

Solving a larger board with a much larger state space (10^25):

# optimal solution length: 100
board = from_rows(
  [17, 1, 20, 9, 16],
  [2, 22, 19, 14, 5],
  [15, 21, 0, 3, 24],
  [23, 18, 13, 12, 7],
  [10, 8, 6, 4, 11]
)
print(search(board, weight=2))
print(search(board, weight=1.5))
print(search(board, weight=1.25))

...
solution_len=134, generated=132468, expanded=73482, unvisited=58987, visited=39738
...
solution_len=118, generated=2517066, expanded=1296158, unvisited=1220909, visited=753608
...
solution_len=108, generated=80558936, expanded=37425835, unvisited=43133102, visited=24834937

We can compare() two heuristics like this:

>>> compare(ha=manhattan_distance, hb=euclidean_distance)
(1594.87, 3377.5)
>>> compare(ha=manhattan_distance, hb=linear_conflict_distance)
(5182.28, 2195.5)

The outputs are the average number of states generated over num_iters runs for each heuristic on the same random set of boards. Default board size used is 3x3 (for the sake of time), but you can pass h / w to change as desired.

Or we can compare two algorithms:

>>> compare(alga="a*", algb="greedy")
(2907.5, 618.0)

Algorithms

>>> list(Algorithm)
[<Algorithm.A_STAR: 'a*'>, <Algorithm.BEAM: 'beam'>, <Algorithm.BFS: 'bfs'>, <Algorithm.DFS: 'dfs'>, <Algorithm.GREEDY: 'greedy'>, <Algorithm.IDA_STAR: 'ida*'>, <Algorithm.IDDFS: 'iddfs'>]

The search() method accepts the enum values or the str name.

The available algorithms are:

• "a*" (default) - Docs, Wiki
• "beam" - Docs, Wiki
• "bfs" - Docs, Wiki
• "dfs" - Docs, Wiki
• "greedy" - Docs, Wiki
• "ida*" - Docs, Wiki
• "iddfs" - Docs, Wiki

All algorithms support behavior customization via kwargs. See the docs for individual algorithms linked above.

Of the provided algorithms, only beam search is incomplete by default. This means it may miss the goal, even thought the board is solvable.

Heuristics

The available heuristics are:

• corner_tiles_heuristic - Adds additional distance penalty when corners are incorrect, but the neighbors are in goal position. Additional moves are needed to shuffle the corners out and the neighbors back. See documentation and comments in code for details about interactions with other heuristics.
• euclidean_distance - The straight line distance in Euclidean space between two tiles.
• hamming_distance - Count of how many tiles are in the correct position
• last_moves_distance - Adds a penalty of 2 if the neighbors of the goal are not located in the goal and the board is unsolved. Can add an additional 2 penalty if the neighbors of the neighbors are also out-of-place. See documentation and comments in code for details about interactions with other heuristics.
• linear_conflict_distance - This is an augmented Manhattan distance. Roughly speaking, adds an additional 2 to each pair of inverted tiles that are already on their goal row/column. (This includes the Manhattan, Last Moves, and Corner Tiles heuristics.)
• manhattan_distance - Count of how many moves it would take each tile to arrive in the correct position, if other tiles could be ignored
• random_distance - This is a random number (but a consistent random number for a given board state). It is useful as a baseline.
• relaxed_adjacency_distance - This is a slight improvement over Hamming distance that includes a penalty for swapping out-of-place tiles.
• Neural net heuristics from slidingpuzzle.nn submodule (see section below)
• Any heuristic you want. Just pass any function that accepts a board and returns a number. The lower the number, the closer the board is to the goal (lower = better).

There are two simple provided utility functions for evaluating algorithm/heuristic performance: evaluate() and compare().

For example, here we use compare() with a trivial custom heuristic to see how it fares against Manhattan Distance:

>>> def max_distance(board):
...     return max(manhattan_distance(board), relaxed_adjacency_distance(board))
...
>>> compare(ha=manhattan_distance, hb=max_distance)
(3020.5, 2857.53)

We can reasonably conclude that on average the max of these two heuristics is slightly better than either one alone (Hansson et al., 1985).

We can use evaluate() to study an algorithm's behavior when tweaking a parameter.

import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(1, 32, num=256)
y = [evaluate(weight=w) for w in x]
plt.plot(x, y)
plt.title("Average Nodes Generated vs. A* Weight")
plt.xlabel("Weight")
plt.ylabel("Generated")
plt.show()

)

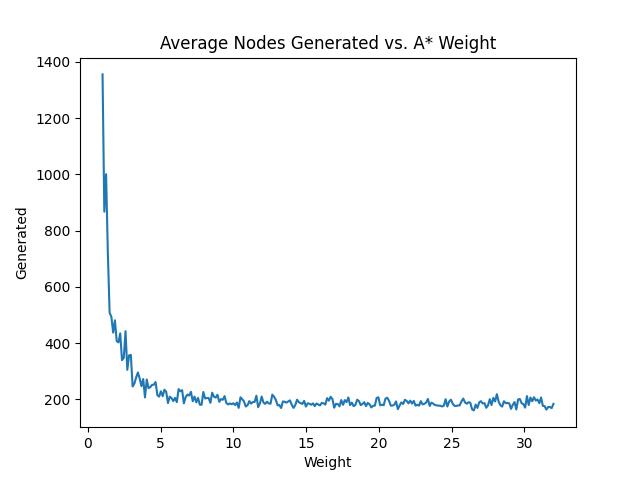Neural Nets

(Download Pretrained Models)

If only wish to use pretrained neural nets:

pip install torch

If want to train nets from scratch using the provided utilities:

pip install -r requirements/nn.txt

Note: This will install a specific tested version of PyTorch. If you want another version, you will need to follow the official PyTorch instructions.

After downloading a model, create a models directory and paste the pt file there. The model is now available. For example:

>>> evaluate(heuristic=nn.v1_distance)
88.75

Well-trained neural networks are far superior to the other heuristics.

To train them yourself, you can generate the datasets locally or download datasets from the HuggingFace link above.

Datasets

(Download Datasets)

You can download existing datasets and use them directly. Place a dataset file into a local directory datasets and it will be available.

If you've downloaded a dataset, you can skip to Train directly. The examples below are for creating new datasets.

You can also build your build your own dataset. Here are some options, from easiest to most difficult:

1. Use reverse BFS to generate all boards in order

examples = nn.generate_examples(4, 4)
nn.save_examples(examples)

1. Randomly sample boards and solve them

examples = nn.random_examples(4, 4, 2**14)
nn.save_examples(examples)

1. Generate all boards in lexicographical order and solve them

examples = []
for board in board_generator(4, 4):
    result = search(board)
    solution = tuple(solution_as_tiles(result.solution))
    examples.append((freeze_board(board), solution))

Note: Code in number 3 is a slight oversimplification. To save more time, you would want to use the intermediate board states as examples. Take a look at the source code for random_examples().

Train

Follow the steps below to train and use your own net from scratch using the models defined in slidingpuzzle.nn.models.

You can then train a new network easily:

import slidingpuzzle.nn as nn
import torch.optim as optim
h, w = 3, 3
dataset = nn.load_dataset(h, w)
nn.set_seed(0)  # if you want reproducible weights
model = nn.Model_v1(h, w)
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=0.9)
nn.train(model, optimizer, dataset)

If you left the default settings for checkpoint_freq, you will now have various model checkpoints available from training.

The model with estimated highest accuracy on the test data is tagged "acc" in the checkpoints directory.

You can evaluate a checkpoint similar to evaluate:

>>> nn.eval_checkpoint(model, tag="acc")
417.71875

Or the latest model epoch:

>>> nn.eval_checkpoint(model, tag="latest", num_iters=128)

The call to eval_checkpoint() will load the model weights from the appropriate checkpoint file and run evaluate().

You can also manually load checkpoints:

>>> checkpoint = nn.load_checkpoint(model, tag="epoch_1499")
>>> checkpoint["epoch"]
1499

(See the checkpoints directory for all trained models available to load by tag.)

You can then register the model:

>>> nn.set_heuristic(model)

Your model is now available as nn.v1_distance if you are using the default provided model Model_v1. (These are associated behind the scenes via the model.version property.)

You can freeze your preferred model to disk to be used as the default for nn.v1_distance:

>>> nn.save_model(model)

Note: Model will be saved into a ./models directory as torchscript. This may overwrite a previously saved model.

The model will now be available whenever you import slidingpuzzle.nn.

>>> compare(ha=nn.v1_distance, hb=linear_conflict_distance, num_iters=256)
(85.43, 1445.38)

By default, training uses GPU if available and falls back to CPU otherwise.

Custom Models

First define your torch.nn.Module somewhere. Your model class must:

• have a unique self.version string that is safe to use in filenames (e.g. "my_model_version")
• have self.h and self.w indicating the input board dimensions it expects,
• have a forward() that accepts a batch of board tensors constructed by:
  • torch.tensor(board, dtype=torch.float32)
  • For example, expect: model(batch)

Train and save your model as above.

You can now copy-paste the model-based heuristic function below:

def my_model_distance(board) -> float:
    h, w = board.shape
    heuristic = nn.get_heuristic(h, w, "my_model_version")
    return heuristic(board)

Just change "my_model_version" to the string you used in your model class.

And you use it as expected:

>>> search(board, "a*", heuristic=my_model_distance)

You can add your my_model_distance() function to the bottom of nn/heuristics.py to make it permanently available.

During training, tensorboard will show your training/test loss and accuracy. After training is complete, you can also evaluate each checkpoint for comparison as shown above.

Contributing

First of all, thanks for contributing! Setup your a standard dev environment using something like conda or venv.

git clone https://github.com/entangledloops/slidingpuzzle.git
cd slidingpuzzle
pip install -e .
pip install -r requirements/dev.txt
pre-commit install

After you've added your new code, verify you haven't broken anything by running pytest:

pytest

If you changed anything in the slidingpuzzle.nn package, also run:

pip install -r requirements/nn.txt
pytest tests/test_nn.py

Don't forget to add new tests for anything you've added.

Finally, check that the docs look correct:

cd docs
make html

Note: Use ./make html on Windows.

You can also run mypy and look for any new violations:

mypy src

Black and flake8 are used for formatting and linting, but they are automatically run by the pre-commit hooks you installed earlier in the Git repo.