A python binding using pybind11 for Sophus, which is a C++ Lie library.(SO3 && SE3)
A python binding using pybind11 for Sophus, which is a C++ Lie library.(SO3 && SE3), used for 2d and 3d geometric problems (i.e. for Computer Vision or Robotics applications)
SophusPy is perfectly compatible with Numpy.
pip install sophuspy
import numpy as np
import sophuspy as sp
# 1. constructor of SO2
sp.SO2() # default
sp.SO2([[1, 0],
[0, 1]]) # list
sp.SO2(np.eye(2)) # numpy
'''
SO2([[1, 0],
[0, 1]])
'''
# 2. constructor of SO3
sp.SO3() # default
sp.SO3([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]]) # list
sp.SO3(np.eye(3)) # numpy
'''
SO3([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]])
'''
# 3. constructor of SE2
sp.SE2() # default
sp.SE2([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]]) # list
sp.SE2(np.eye(3)) # numpy
'''
SE2([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]])
'''
# 4. constructor of SE3
sp.SE3() # default
sp.SE3([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]]) # list
sp.SE3(np.eye(4)) # numpy
'''
SE3([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]])
'''
# 5. R, t constructor of SE2
sp.SE2(np.eye(2), np.ones(2)) # R, t
'''
SE2([[1, 0, 1],
[0, 1, 1],
[0, 0, 1]])
'''
# 6. R, t constructor of SE3
sp.SE3(np.eye(3), np.ones(3)) # R, t
'''
SE3([[1, 0, 0, 1],
[0, 1, 0, 1],
[0, 0, 1, 1],
[0, 0, 0, 1]])
'''
R = sp.SO3()
R1 = sp.SO3([[0, 1, 0],
[0, 0, 1],
[1, 0, 0]])
# 1. SO3 * SO3
R * R1
'''
SO3([[0, 1, 0],
[0, 0, 1],
[1, 0, 0]])
'''
# 2.
R1 *= R
T = sp.SE3()
T1 = sp.SE3(R1.matrix(), np.ones(3))
# 3. SE3 * SE3
T * T1
'''
SE3([[0, 1, 0, 1],
[0, 0, 1, 1],
[1, 0, 0, 1],
[0, 0, 0, 1]])
'''
# 4.
T1 *= T
R = sp.SO2([[0, -1],
[1, 0]])
T = sp.SE2(R.matrix(), np.ones(2))
pt = np.array([1, 2])
pts = np.array([[1, 2],
[3, 4]])
# 1. single point
R * pt # array([-2., 1.])
# 2. N points
R * pts # array([[-2., 1.],
# [-4., 3.]])
# 3. single point
T * pt # array([-1., 2.])
# 4. N points
T * pts # array([[-1., 2.],
# [-3., 4.]])
R = sp.SO3([[0, 1, 0],
[0, 0, 1],
[1, 0, 0]])
T = sp.SE3(R.matrix(), np.ones(3))
pt = np.array([1, 2, 3])
pts = np.array([[1, 2, 3],
[4, 5, 6]])
# 1. single point
R * pt # array([2., 3., 1.])
# 2. N points
R * pts # array([[2., 3., 1.],
# [5., 6., 4.]])
# 3. single point
T * pt # array([3., 4., 2.])
# 4. N points
T * pts # array([[3., 4., 2.],
# [6., 7., 5.]])
R = sp.SO3([[0, 1, 0],
[0, 0, 1],
[1, 0, 0]])
T = sp.SE3(R.matrix(), np.ones(3))
# 1.
R.matrix()
'''
array([[0., 1., 0.],
[0., 0., 1.],
[1., 0., 0.]])
'''
# 2.
R.log() # array([-1.20919958, -1.20919958, -1.20919958])
# 3.
R.inverse()
'''
SO3([[0, 0, 1],
[1, 0, 0],
[0, 1, 0]])
'''
# 4.
R.copy()
# 5.
T.matrix()
'''
array([[0., 1., 0., 1.],
[0., 0., 1., 1.],
[1., 0., 0., 1.],
[0., 0., 0., 1.]])
'''
# 6.
T.matrix3x4()
'''
array([[0., 1., 0., 1.],
[0., 0., 1., 1.],
[1., 0., 0., 1.]])
'''
T_SE2.matrix2x3() # For SE2
# 7.
T.so3()
'''
SO3([[0, 1, 0],
[0, 0, 1],
[1, 0, 0]])
'''
# 8.
T.log() # array([1., 1., 1., -1.20919958, -1.20919958, -1.20919958])
# 9.
T.inverse()
'''
SE3([[ 0, 0, 1, -1],
[ 1, 0, 0, -1],
[ 0, 1, 0, -1],
[ 0, 0, 0, 1]])
'''
# 10.
T.copy()
# 11.
T.translation() # array([1., 1., 1.])
# 12.
T.rotationMatrix()
'''
array([[0., 1., 0.],
[0., 0., 1.],
[1., 0., 0.]])
'''
# 13.
T.setRotationMatrix(np.eye(3)) # set SO3 matrix
# 14.
T.setTranslation(np.zeros(3)) # set translation
sp.SO2.hat(1)
'''
array([[ 0., -1.],
[ 1., 0.]])
'''
sp.SO3.hat(np.ones(3))
'''
array([[ 0., -1., 1.],
[ 1., 0., -1.],
[-1., 1., 0.]])
'''
sp.SO2.exp(1)
'''
SO2([[ 0.54030230586814, -0.841470984807897],
[ 0.841470984807897, 0.54030230586814]])
'''
sp.SO3.exp(np.ones(3))
'''
array([[ 0.22629564, -0.18300792, 0.95671228],
[ 0.95671228, 0.22629564, -0.18300792],
[-0.18300792, 0.95671228, 0.22629564]])
'''
sp.SE2.hat(np.ones(3))
'''
array([[ 0., -1., 1.],
[ 1., 0., 1.],
[ 0., 0., 0.]])
'''
sp.SE3.hat(np.ones(6))
'''
array([[ 0., -1., 1., 1.],
[ 1., 0., -1., 1.],
[-1., 1., 0., 1.],
[ 0., 0., 0., 0.]])
'''
sp.SE2.exp(np.ones(3))
'''
SE2([[ 0.54030230586814, -0.841470984807897, 0.381773290676036],
[ 0.841470984807897, 0.54030230586814, 1.30116867893976],
[ 0, 0, 1]])
'''
sp.SE3.exp(np.ones(6))
'''
array([[ 0.22629564, -0.18300792, 0.95671228, 1. ],
[ 0.95671228, 0.22629564, -0.18300792, 1. ],
[-0.18300792, 0.95671228, 0.22629564, 1. ],
[ 0. , 0. , 0. , 1. ]])
'''
# 1. copy SO3
sp.copyto(R, R1) # copytoSO3(SO3d &dst, const SO3d &src)
# 2. copy SE3
sp.copyto(T, T1) # copytoSE3(SE3d &dst, const SE3d &src)
# 3.if R is not a strict rotation matrix, normalize it. Uses Eigen3
# Eigen::Quaterniond q(R);
# q.normalized().toRotationMatrix();
R_matrix = np.array([[1. , 0.001, 0. ],
[0. , 1. , 0. ],
[0. , 0. , 1. ]])
sp.to_orthogonal(R_matrix)
sp.to_orthogonal_3d(R_matrix) # the same as to_orthogonal
'''
array([[ 9.99999875e-01, 4.99999969e-04, 0.00000000e+00],
[-4.99999969e-04, 9.99999875e-01, -0.00000000e+00],
[-0.00000000e+00, 0.00000000e+00, 1.00000000e+00]])
'''
# if R(2D) is not a strict rotation matrix, normalize it. Uses Eigen3
# Eigen::Rotation2Dd rotation;
# rotation.fromRotationMatrix(R);
# rotation.toRotationMatrix();
sp.to_orthogonal_2d(matrix2x2) # 2D verison to_orthogonal
# 4. invert N poses in a row
pose = T.matrix3x4().ravel() # array([1., 0., 0., 0., 0., 1., 0., 0., 0., 0., 1., 0.])
sp.invert_poses(pose) # array([1., 0., 0., 0., 0., 1., 0., 0., 0., 0., 1., 0.]) identity matrix returns the same
poses = np.array([[1., 0., 0., 0., 0., 1., 0., 0., 0., 0., 1., 0.],
[0., 1., 0., 1., 0., 0., 1., 1., 1., 0., 0., 1.]])
sp.invert_poses(poses)
'''
array([[ 1., 0., 0., -0., 0., 1., 0., -0., 0., 0., 1., -0.],
[ 0., 0., 1., -1., 1., 0., 0., -1., 0., 1., 0., -1.]])
'''
# 6. transform N points by M poses to form N * M points
points = np.array([[1., 2., 3.],
[4., 5., 6.],
[7., 8., 9.]])
sp.transform_points_by_poses(poses, points)
'''
array([[ 1., 2., 3.],
[ 4., 5., 6.],
[ 7., 8., 9.],
[ 3., 4., 2.],
[ 6., 7., 5.],
[ 9., 10., 8.]])
'''
FAQs
A python binding using pybind11 for Sophus, which is a C++ Lie library.(SO3 && SE3)
We found that sophuspy demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?
Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.
Security News
Research
The Socket Research Team breaks down a malicious wrapper package that uses obfuscation to harvest credentials and exfiltrate sensitive data.
Research
Security News
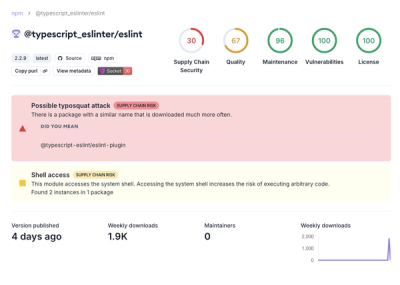
Attackers used a malicious npm package typosquatting a popular ESLint plugin to steal sensitive data, execute commands, and exploit developer systems.
Security News
The Ultralytics' PyPI Package was compromised four times in one weekend through GitHub Actions cache poisoning and failure to rotate previously compromised API tokens.