
Security News
Research
Data Theft Repackaged: A Case Study in Malicious Wrapper Packages on npm
The Socket Research Team breaks down a malicious wrapper package that uses obfuscation to harvest credentials and exfiltrate sensitive data.
You can get statinf from PyPI with:
pip install statinf
statinf is a library for statistics and causal inference.
It provides main the statistical models ranging from the traditional OLS to Neural Networks.
The library is supported on Windows, Linux and MacOs.
You can find the full documentation at https://www.florianfelice.com/statinf.
You can also find an FAQ and the latest news of the library on the documentation.
Here is a non-exhaustive list of available modules on statinf:
MLP implements MultiLayer Perceptron
(see MLP for more details and examples).
OLS allows to use Ordinary Least Squares for linear regressions
(see OLS for more details and examples).
GLM implements the Generalized Linear Models
see GLM for more details and examples).
stats allows to use descriptive and
tests statistics.
data is a module to process data such as data generation,
One Hot Encoding and others
(see data processing or (see data generation modules for more details).
You can find the below examples and many more on https://www.florianfelice.com/statinf. Stay tuned with the future releases.
statinf comes with the OLS regression implemented with the analytical formula:
from statinf.regressions import OLS
from statinf.data import generate_dataset
# Generate a synthetic dataset
data = generate_dataset(coeffs=[1.2556, -0.465, 1.665414, 2.5444, -7.56445], n=1000, std_dev=1.6)
# We set the OLS formula
formula = "Y ~ X0 + X1 + X2 + X3 + X4 + X1*X2 + exp(X2)"
# We fit the OLS with the data, the formula and without intercept
ols = OLS(formula, df, fit_intercept=True)
ols.summary()
The output will be:
==================================================================================
| OLS summary |
==================================================================================
| R² = 0.98475 | R² Adj. = 0.98464 |
| n = 999 | p = 7 |
| Fisher value = 10676.727 | |
==================================================================================
| Variables | Coefficients | Std. Errors | t-values | Probabilities |
==================================================================================
| X0 | 1.3015 | 0.03079 | 42.273 | 0.0 *** |
| X1 | -0.48712 | 0.03123 | -15.597 | 0.0 *** |
| X2 | 1.62079 | 0.04223 | 38.377 | 0.0 *** |
| X3 | 2.55237 | 0.0326 | 78.284 | 0.0 *** |
| X4 | -7.54776 | 0.03247 | -232.435 | 0.0 *** |
| X1*X2 | 0.03626 | 0.02866 | 1.265 | 0.206 |
| exp(X2) | -0.00929 | 0.01551 | -0.599 | 0.549 |
==================================================================================
| Significance codes: 0. < *** < 0.001 < ** < 0.01 < * < 0.05 < . < 0.1 < '' < 1 |
The logistic regression can be used for binary classification where follows a Bernoulli distribution. With
being the matrix of regressors, we have:
We then implement the regression with:
from statinf.regressions import GLM
from statinf.data import generate_dataset
# Generate a synthetic dataset
data = generate_dataset(coeffs=[1.2556, -6.465, 1.665414, -1.5444], n=2500, std_dev=10.5, binary=True)
# We split data into train/test/application
train = data.iloc[0:1000]
test = data.iloc[1001:2000]
# We set the linear formula for Xb
formula = "Y ~ X0 + X1 + X2 + X3"
logit = GLM(formula, train, test_set=test)
# Fit the model
logit.fit(plot=False, maxit=10)
logit.get_weights()
The ouput will be:
==================================================================================
| Logit summary |
==================================================================================
| McFadden R² = 0.67128 | McFadden R² Adj. = 0.6424 |
| Log-Likelihood = -227.62 | Null Log-Likelihood = -692.45 |
| LR test p-value = 0.0 | Covariance = nonrobust |
| n = 999 | p = 5 |
| Iterations = 8 | Convergence = True |
==================================================================================
| Variables | Coefficients | Std. Errors | t-values | Probabilities |
==================================================================================
| X0 | -1.13024 | 0.10888 | -10.381 | 0.0 *** |
| X1 | 0.02963 | 0.07992 | 0.371 | 0.711 |
| X2 | -1.40968 | 0.1261 | -11.179 | 0.0 *** |
| X3 | 0.5253 | 0.08966 | 5.859 | 0.0 *** |
==================================================================================
| Significance codes: 0. < *** < 0.001 < ** < 0.01 < * < 0.05 < . < 0.1 < '' < 1 |
==================================================================================
You can train a Neural Network using the MLP class.
The below example shows how to train an MLP with 1 single linear layer. It is equivalent to implement an OLS with Gradient Descent.
from statinf.data import generate_dataset
from statinf.ml import MLP, Layer
# Generate the synthetic dataset
data = generate_dataset(coeffs=[1.2556, -6.465, 1.665414, 1.5444], n=1000, std_dev=1.6)
Y = ['Y']
X = [c for c in data.columns if c not in Y]
# Initialize the network and its architecture
nn = MLP()
nn.add(Layer(4, 1, activation='linear'))
# Train the neural network
nn.train(data=data, X=X, Y=Y, epochs=1, learning_rate=0.001)
# Extract the network's weights
print(nn.get_weights())
Output:
{'weights 0': array([[ 1.32005564],
[-6.38121934],
[ 1.64515704],
[ 1.48571785]]), 'bias 0': array([0.81190412])}
FAQs
A library for statistics and causal inference
We found that statinf demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Security News
Research
The Socket Research Team breaks down a malicious wrapper package that uses obfuscation to harvest credentials and exfiltrate sensitive data.
Research
Security News
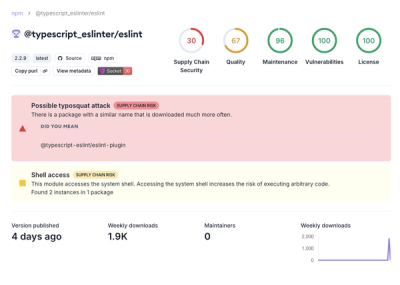
Attackers used a malicious npm package typosquatting a popular ESLint plugin to steal sensitive data, execute commands, and exploit developer systems.

Security News
The Ultralytics' PyPI Package was compromised four times in one weekend through GitHub Actions cache poisoning and failure to rotate previously compromised API tokens.