
Security News
Research
Data Theft Repackaged: A Case Study in Malicious Wrapper Packages on npm
The Socket Research Team breaks down a malicious wrapper package that uses obfuscation to harvest credentials and exfiltrate sensitive data.
A simple python wrapper around Binary Decision Diagrams (BDDs) to interpret them as Deterministic Finite Automata (DFAs).
The package takes as input a BDD from the dd package
and returns a DFA from the dfa package.
Formally, the resulting DFA objects are quasi-reduced BDDs (QDDs)
where all leaves self loop and the label of states is a tuple: (int, str | bool), where the first entry determines the number of inputs until this node is active and the second entry is the decision variable of the node or the BDD's truth assignment.
Table of Contents
If you just need to use bdd2dfa, you can just run:
$ pip install bdd2dfa
For developers, note that this project uses the poetry python package/dependency management tool. Please familarize yourself with it and then run:
$ poetry install
# Create BDD
from dd import BDD
manager = BDD()
manager.declare('x', 'y', 'z')
x, y, z = map(manager.var, 'xyz')
bexpr = x & y & z
# Convert to DFA
from bdd2dfa import to_dfa
qdd = to_dfa(bexpr)
assert len(qdd.states()) == 7
# End at leaf node.
assert qdd.label([1, 1, 1]) == (0, True)
assert qdd.label([0, 1, 1]) == (0, False)
# End at Non-leaf node.
assert qdd.label([1, 1]) == (0, 'z')
assert qdd.label([0, 1]) == (1, False)
# leaf nodes are self loops.
assert qdd.label([1, 1, 1, 1]) == (0, True)
assert qdd.label([1, 1, 1, 1, 1]) == (0, True)
Each state of the resulting DFA object has three attribute:
node: A reference to the internal BDD node given by dd.parity: dd supports Edge Negated BDDs, where some edges point
to a Boolean function that is the negation of the Boolean function
the node would point to in a standard BDD. Parity value determines
whether or not the nodedebt: Number of inputs needed before this node can
transition. Required since BDD edges can skip over irrelevant
decisions.For example,
assert qdd.start.parity is True
assert qdd.start.debt == 0
assert qdd.start.node.var == 'x'
to_dfa also supports exporting a BDD rather than a QDD. This is done
by toggling the qdd flag.
bdd = to_dfa(bexpr, qdd=False)
The DFA uses a similar state as the QDD case, but does not have a
debt attribute. Useful when one just wants to walk the BDD.
note The labeling alphabet also only returns the decision variable/truth assignment.
If the dfa package was installed with the draw option, we can
visualize the difference between qdd and bdd by exporting to a
graphviz dot file.
from dfa.draw import write_dot
write_dot(qdd, "qdd.dot")
write_dot(bdd, "bdd.dot")
Compiling using the dot command yields the following for qdd.dot
and the following for bdd.dot:
FAQs
Python library for converting binary decision diagrams to automata.
We found that bdd2dfa demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Security News
Research
The Socket Research Team breaks down a malicious wrapper package that uses obfuscation to harvest credentials and exfiltrate sensitive data.
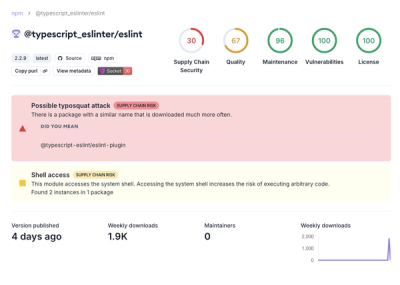
Research
Security News
Attackers used a malicious npm package typosquatting a popular ESLint plugin to steal sensitive data, execute commands, and exploit developer systems.

Security News
The Ultralytics' PyPI Package was compromised four times in one weekend through GitHub Actions cache poisoning and failure to rotate previously compromised API tokens.