Product
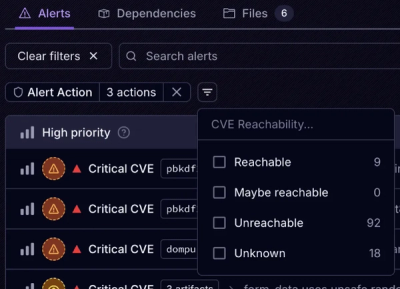
Introducing Tier 1 Reachability: Precision CVE Triage for Enterprise Teams
Socket’s new Tier 1 Reachability filters out up to 80% of irrelevant CVEs, so security teams can focus on the vulnerabilities that matter.
Supported highly optimized and flexible genetic algorithm package for python
https://pasaopasen.github.io/geneticalgorithm2/
geneticalgorithm2 (from DPEA) is the supported advanced optimized fork of non-supported package geneticalgorithm of Ryan (Mohammad) Solgi
geneticalgorithm package)geneticalgorithm2 is very flexible and highly optimized Python library for implementing classic genetic-algorithm (GA).
Features of this package:
Install this package with standard light dependencies to use the base functional.
pip install geneticalgorithm2
Install this package with full dependencies to use all provided functional including plotting and built-in parallelism tools.
pip install geneticalgorithm2[full]
MiddleCallbacks and removed as alone run() parametersvartype will support strings like iiiiibbffunction_timeout and function to run() method and deprecate its usage in init()function is not mandatory to be non-emptygeneticalgorithm2 class to GeneticAlgorithm2pip install geneticalgorithm2[full] versionOppOpPopInit 2.0.0->2.0.1function_timeout to None which means no use of function time checkingjoblib and func_timeout from necessary dependenciesfill_children(pop_matrix, parents_count) to geneticalgorithm2 class to specify children creating behavior (what is the most intensive part of algorithm after optimizing func calculations), see this'stderr' or 'stdout' or None (disable) by choice (progress_bar_stream argument of run()), deprecated disable_progress_bargeneticalgorithm2.vectorized_set_function set function, which can be faster for big populationscrossover_probability model parameter because of it has no sense to exist (and 1.0 value is better than others, take a look at results). This parameter came from geneticalgorithm old package and did`t change before.variable_type=='bool'setup.pyPROGRESS_BAR_LEN field of geneticalgorithm2 class)run(), more informative outputrun() method fastershow mean parameter from model.plot_result and now model reports only best score by default, not average and so on (u can specify if u wanna report average too)plot_several_lines useful functionmutation_discrete_type and mutation_discrete_probability parameters in model. It controls mutation behavior for discrete (integer) variables and works like mutation_type and mutation_probability work for continuous (real) variables. Take a look at algorithm parametersvariable_type_mixed, now use variable_type for mixed optimization toooutput_dict, now it's better object with name resultcollections.Sequence with collections.abc.Sequence, now it should work for python3.10+MiddleCallbackData dataclass instead of dictionary)start_generation; now it's valid to use
Nonestr path to saved generation{'variables': variables/None, 'scores': scores/None}Generation object: Generation(variables = variables, scores = scores)np.ndarray with shape (samples, dim) for only population or (samples, dim+1) for concatenated population and score (scores is the last matrix column)tuple(np.ndarray/None, np.ndarray/None) for variables and scoresvariables is 2D numpy array with shape (samples, dim), scores is 1D numpy array with scores (function values) for each sample; here and here u can see examples of using these valid formsAlgorithmParams class for base GA algorithm parameters (instead of dictionary)Generation class for saving/loading/returning generation (instead of dictionary)All that classes are collected in file. To maintain backward compatibility, AlgorithmParams and Generation classes have dictionary-like interface for getting fields: u can use object.field or object['field'] notations.
Pre-process: making inner functions depends on params, making/loading start population
while True:
if reason to stop (time is elapsed / no progress / generation count is reached / min value is reached):
break
select parents to crossover from last population and put them to new population:
select (elit count) best samples
select (parents count - elit count) random samples (by selection function)
create (total samples count - parents count) children (samples from selected parents) and put them to new population:
while not all children are created:
select 2 random parents
make child1, child2 from them using crossover
mutate child1 by mutation (model.mut)
mutate child2 by middle mutation (model.mut_middle)
put children to new population
remove duplicates, make revolutions, sort population by scores
use callbacks, use middle callbacks
Post-process: plotting results, saving
The goal of the optimization process is to find the minimum of the given function (1D array) -> float where the function argument is a vector of some values in different dimensions.
If u want to find the maximum, use this idea:
opt_func = lambda arr: -func(arr)
#
# ... find global min of opt_func
#
opt_minimum=opt_func(best value)
maximum = -opt_minimum
Also it is possible and highly recommended to create and use a vectorized version of this function called set_function (2D array) -> (1D array) which transforms several samples matrix to samples scores vector by one call. Using this way u can speed up calculations or set up more complex tasks optimization
The function rates 1D arrays (vectors) where each component (dimension) means something u program it to mean. Each dimension has its bound ([min; max] cut) and variable type (real/discrete).
Advice. Genetic algorithms work much faster and efficient for discrete tasks. If high precision is not required u can split any real dimension to many discrete values (for instance, [1.1, 1.2, 1.25, 1.44]) and try to optimize indexes of the given array which are converted to real values inside function itself.
There are a number of hyperparameters u can probe to optimize including population size and selection/crossover/mutation types.
There are several ways to create new testing samples from zero when u start with empty population or when u need new samples after duplicates removing and revolutions.
Now the package supports 2 different types of highly customized callbacks:
Firstly, u should import needed packages.
All available (but not always necessary) imports are:
import numpy as np
# the only one required import
from geneticalgorithm2 import GeneticAlgorithm2 as ga # for creating and running optimization model
from geneticalgorithm2 import Generation, AlgorithmParams # classes for comfortable parameters setting and getting
from geneticalgorithm2 import Crossover, Mutations, Selection # classes for specific mutation and crossover behavior
from geneticalgorithm2 import get_population_initializer # for creating better start population
from geneticalgorithm2 import np_lru_cache # for cache function (if u want)
from geneticalgorithm2 import plot_pop_scores # for plotting population scores, if u want
from geneticalgorithm2 import Callbacks # simple callbacks (will be deprecated)
from geneticalgorithm2 import Actions, ActionConditions, MiddleCallbacks # middle callbacks
Next step: define the function to minimize:
def function(X: np.ndarray) -> float: # X as 1d-numpy array
return np.sum(X**2) + X.mean() + X.min() + X[0]*X[2] # some float result
Also u should create the bounds for each variable (if exist) such as:
var_bound = np.array([[0,10]]*3) # 2D numpy array with shape (dim, 2)
# also u can use Sequence of Tuples (from version 6.3.0)
var_bound = [
(0, 10),
(0, 10),
(0, 10)
]
Important. U don't need to use variable boundaries only if variable type of each variable is boolean. This case will be automatically converted to discrete variables with bounds (0, 1).
After that u create a GeneticAlgorithm2 (was imported early as ga) object:
model = ga(
dimension = 3,
variable_type='real',
variable_boundaries = var_bound,
algorithm_parameters={
'max_num_iteration': None,
'population_size':100,
'mutation_probability': 0.1,
'mutation_discrete_probability': None,
'elit_ratio': 0.01,
'parents_portion': 0.3,
'crossover_type':'uniform',
'mutation_type': 'uniform_by_center',
'mutation_discrete_type': 'uniform_discrete',
'selection_type': 'roulette',
'max_iteration_without_improv':None
}
)
Note: it is not mandatory to write all possible algorithm_parameters, here it is done only to show u defaults. Also u can use AlgorithmParams (with typehints and docstrings) class instead of dicts:
algorithm_parameters=AlgorithmParams(
max_num_iteration=None,
population_size=100,
mutation_probability=0.1,
mutation_discrete_probability=None,
elit_ratio=0.01,
parents_portion=0.3,
crossover_type='uniform',
mutation_type='uniform_by_center',
mutation_discrete_type='uniform_discrete',
selection_type='roulette',
max_iteration_without_improv=None
)
Run the search method:
# all of this parameters are default
result = model.run(
no_plot = False,
progress_bar_stream = 'stdout',
disable_printing = False,
function=function,
function_timeout=None,
set_function = None,
apply_function_to_parents = False,
start_generation = None,
studEA = False,
mutation_indexes = None,
init_creator = None,
init_oppositors = None,
duplicates_oppositor = None,
remove_duplicates_generation_step = None,
revolution_oppositor = None,
revolution_after_stagnation_step = None,
revolution_part = 0.3,
population_initializer = Population_initializer(select_best_of = 1, local_optimization_step = 'never', local_optimizer = None),
stop_when_reached = None,
callbacks = [],
middle_callbacks = [],
time_limit_secs = None,
save_last_generation_as = None,
seed = None
)
# best candidate
print(result.variable)
# best score
print(result.score)
# last generation
print(result.last_generation)
Have a look at https://pasaopasen.github.io/geneticalgorithm2/geneticalgorithm2/geneticalgorithm2.html#GeneticAlgorithm2.__init__
The parameters of GA is defined as a dictionary or AlgorithmParams object: https://pasaopasen.github.io/geneticalgorithm2/geneticalgorithm2/data_types/algorithm_params.html
To get the global default params use code:
params = ga.default_params
To get actual parameters of an existing model use code:
params = model.param
https://pasaopasen.github.io/geneticalgorithm2/geneticalgorithm2/crossovers.html
https://pasaopasen.github.io/geneticalgorithm2/geneticalgorithm2/mutations.html
https://pasaopasen.github.io/geneticalgorithm2/geneticalgorithm2/selections.html
Have a look at https://pasaopasen.github.io/geneticalgorithm2/geneticalgorithm2/geneticalgorithm2.html#GeneticAlgorithm2.run
Assume we want to find a set of X = (x1, x2, x3) that minimizes function f(X) = x1 + x2 + x3 where X can be any real number in [0, 10].
This is a trivial problem and we already know that the answer is X = (0, 0, 0) where f(X) = 0.
We just use this simple example to show how to implement it with geneticalgorithm2. First we import geneticalgorithm2 and numpy. Next, we define
function f which we want to minimize and the boundaries of the decision variables. Then simply geneticalgorithm2 is called to solve the defined optimization problem as follows:
import numpy as np
from geneticalgorithm2 import GeneticAlgorithm2 as ga
def f(X):
return np.sum(X)
varbound = [[0, 10]] * 3
model = ga(dimension=3, variable_type='real', variable_boundaries=varbound)
model.run(function=f)
If you run the code, you should see a progress bar that shows the progress of the genetic algorithm (GA) and then the solution, objective function value and the convergence curve as follows:

Also we can access to the best answer of the defined optimization problem found by GA as a dictionary and a report of the progress of the genetic algorithm. To do so we complete the code as follows:
convergence = model.report
solution = model.result
Considering the problem given in the simple example above.
Now assume all variables are integers. So x1, x2, x3 can be any integers in [0, 10].
In this case the code is as the following:
import numpy as np
from geneticalgorithm2 import GeneticAlgorithm2 as ga
def f(X):
return np.sum(X)
varbound = [[0, 10]] * 3
model = ga(dimension=3, variable_type='int', variable_boundaries=varbound)
model.run(function=f)
So, as it is seen the only difference is that for variable_type we use string 'int'.
Considering the problem given in the simple example above.
Now assume all variables are boolean instead of real or integer. So X can be either zero or one. Also instead of three let's have 30 variables.
In this case the code is as the following:
import numpy as np
from geneticalgorithm2 import GeneticAlgorithm2 as ga
def f(X):
return np.sum(X)
model = ga(dimension=30, variable_type='bool')
model.run(function=f)
Note for variable_type we use string 'bool' when all variables are boolean.
Note that when variable_type equal 'bool' there is no need for variable_boundaries to be defined.
Considering the problem given in the the simple example above where we want to minimize f(X) = x1 + x2 + x3.
Now assume x1 is a real (continuous) variable in [0.5; 1.5], x2 is an integer variable in [1;100], and x3 is a boolean variable that can be either zero or one.
We already know that the answer is X = (0.5, 1, 0) where f(X) = 1.5.
We implement geneticalgorithm2 as the following:
import numpy as np
from geneticalgorithm2 import GeneticAlgorithm2 as ga
def f(X):
return np.sum(X)
varbound = [[0.5, 1.5], [1, 100], [0, 1]]
vartype = ('real', 'int', 'int')
model = ga(dimension=3, variable_type=vartype, variable_boundaries=varbound)
model.run(function=f)
In all above examples, the optimization problem was unconstrained. Now consider that we want to minimize f(X) = x1+x2+x3 where X is a set of real variables in [0; 10]. Also we have an extra constraint so that sum of x1 and x2 is equal or greater than 2. The minimum of f(X) is 2.
In such a case, a trick is to define penalty function. Hence we use the code below:
import numpy as np
from geneticalgorithm2 import GeneticAlgorithm2 as ga
def f(X):
pen = 0
if X[0] + X[1] < 2:
pen = 500 + 1000 * (2 - X[0] - X[1])
return np.sum(X) + pen
varbound = [[0, 10]] * 3
model = ga(dimension=3, variable_type='real', variable_boundaries=varbound)
model.run(function=f)
As seen above we add a penalty to the objective function whenever the constraint is not met.
Some hints about how to define a penalty function:
f(X)=300). So I chose a constant of 500. So, if a trial solution is not in the feasible region even though its objective function may be small, the penalized objective function (fitness function) is worse than any feasible solution.For some task u need to think a lot and create good specific crossover or mutation functions. For example, take a look at this problem:
From set like X = {x1, x2, x3, ..., xn} u should select only k objects which get the best function value
U can do it using this code:
import numpy as np
from geneticalgorithm2 import GeneticAlgorithm2 as ga
subset_size = 20 # how many objects we can choose
objects_count = 100 # how many objects are in set
my_set = np.random.random(objects_count) * 10 - 5 # set values
# minimized function
def f(X):
return abs(np.mean(my_set[X == 1]) - np.median(my_set[X == 1]))
# initialize start generation and params
N = 1000 # size of population
start_generation = np.zeros((N, objects_count))
indexes = np.arange(0, objects_count, dtype=np.int8) # indexes of variables
for i in range(N):
inds = np.random.choice(indexes, subset_size, replace=False)
start_generation[i, inds] = 1
def my_crossover(parent_a, parent_b):
a_indexes = set(indexes[parent_a == 1])
b_indexes = set(indexes[parent_b == 1])
intersect = a_indexes.intersection(b_indexes) # elements in both parents
a_only = a_indexes - intersect # elements only in 'a' parent
b_only = b_indexes - intersect
child_inds = np.array(list(a_only) + list(b_only), dtype=np.int8)
np.random.shuffle(child_inds) # mix
children = np.zeros((2, parent_a.size))
if intersect:
children[:, np.array(list(intersect))] = 1
children[0, child_inds[:int(child_inds.size / 2)]] = 1
children[1, child_inds[int(child_inds.size / 2):]] = 1
return children[0, :], children[1, :]
model = ga(
dimension=objects_count,
variable_type='bool',
algorithm_parameters={
'max_num_iteration': 500,
'mutation_probability': 0, # no mutation, just crossover
'elit_ratio': 0.05,
'parents_portion': 0.3,
'crossover_type': my_crossover,
'max_iteration_without_improv': 20
}
)
model.run(
function=f,
no_plot=False,
start_generation=(start_generation, None)
)
For two example parents (one with ones and one with zeros) next crossovers will give same children (examples):
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.87 | 0.87 | 0.87 | 0.87 | 0.87 | 0.87 | 0.87 | 0.87 | 0.87 | 0.87 | 0.87 | 0.87 | 0.87 | 0.87 | 0.87 |
| 0.63 | 0.84 | 1.1 | 0.73 | 0.67 | -0.19 | 0.3 | 0.72 | -0.18 | 0.61 | 0.84 | 1.14 | 1.36 | -0.37 | -0.19 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.51 | 0.58 | 0.43 | 0.42 | 0.55 | 0.49 | 0.57 | 0.48 | 0.46 | 0.56 | 0.56 | 0.54 | 0.44 | 0.51 | 0.4 |

geneticalgorithm2 inherited several features from geneticalgorithm package sush as that if the given function does not provide any output before timeout, the algorithm would be terminated and raise the appropriate error.
In such a case make sure the given function works correctly (i.e. there is no infinite loop in the given function). Also if the given function takes more than 10 seconds to complete the work
make sure to increase function_timeout in arguments.
The convergence curve of an elitist genetic algorithm is always non-increasing. So, the best ever found solution is equal to the best solution of the last iteration. However, the convergence curve of a standard genetic algorithm is different. If elit_ratio is zero geneticalgorithm2 implements a standard GA. The output of geneticalgorithm2 for standard GA is the best ever found solution not the solution of the last iteration. The difference between the convergence curve of standard GA and elitist GA is shown below:

Stud EA is the idea of using crossover always with best object. So one of two parents is always the best object of population. It can help us in a lot of tasks!

There is get_population_initializer(select_best_of = 4, local_optimization_step = 'never', local_optimizer = None) function for creating start population creators. Take a look at its docs
This little option can help u especially with multimodal tasks.

We can apply some local optimization on start generation before starting GA search. It can be some gradient descent or hill climbing and so on. Also we can apply it before selection best objects (on entire population) or after (on best part of population) and so forth.
In next example I'm using my DiscreteHillClimbing algorithm for local optimization my discrete task:
import numpy as np
import matplotlib.pyplot as plt
from DiscreteHillClimbing import Hill_Climbing_descent
from geneticalgorithm2 import GeneticAlgorithm2 as ga
from geneticalgorithm2 import get_population_initializer
def f(arr):
arr2 = arr / 25
return -np.sum(arr2 * np.sin(np.sqrt(np.abs(arr2)))) ** 5 + np.sum(np.abs(arr2)) ** 2
iterations = 100
varbound = [[-100, 100]] * 15
available_values = [np.arange(-100, 101)] * 15
my_local_optimizer = lambda arr, score: Hill_Climbing_descent(
function=f, available_predictors_values=available_values,
max_function_evals=50, start_solution=arr
)
model = ga(
dimension=varbound.shape[0],
variable_type='int',
variable_boundaries=varbound,
algorithm_parameters={
'max_num_iteration': iterations,
'population_size': 400
}
)
for time in ('before_select', 'after_select', 'never'):
model.run(
function=f
no_plot=True,
population_initializer=get_population_initializer(
select_best_of=3,
local_optimization_step=time,
local_optimizer=my_local_optimizer
)
)
plt.plot(model.report, label=f"local optimization time = '{time}'")
plt.xlabel('Generation')
plt.ylabel('Minimized function (40 simulations average)')
plt.title('Selection best N object before running GA')
plt.legend()

Also u can create start population with oppositions. See example of code

U can create revolutions in your population after some stagnation steps. It really can help u for some tasks. See example

If u remove duplicates each k generations, u can speed up the optimization process (example)

It can be useful for run-speed to use cache with some discrete tasks. For this u can import np_lru_cache decorator and use it like here:
import np_lru_cache
@np_lru_cache(maxsize=some_size)
def minimized_func(arr):
# code
return result
#
# run
# algorithm
#
# don't forget to clear cache
minimized_func.cache_clear()
Basically the model checks best population score (minimal score of generation) each generation and saves it to report field. Actually this sequence of numbers u see in big part of plots. This behavior is needed for several parts and u cannot disable it. But if u want to report some other metric without using callbacks, there is highly simple and fast way.
After creating model but before running run() u need to append ur logic to model.checked_reports field. Take a look at example:
import numpy as np
from geneticalgorithm2 import GeneticAlgorithm2 as ga
from geneticalgorithm2 import plot_several_lines
def f(X):
return 50 * np.sum(X) - np.sum(np.sqrt(X) * np.sin(X))
dim = 25
varbound = [[0, 10]] * dim
model = ga(
dimension=dim,
variable_type='real',
variable_boundaries=varbound,
algorithm_parameters={
'max_num_iteration': 600
}
)
# here model exists and has checked_reports field
# now u can append any functions to report
model.checked_reports.extend(
[
('report_average', np.mean),
('report_25', lambda arr: np.quantile(arr, 0.25)),
('report_50', np.median)
]
)
# run optimization process
model.run(
function=f,
no_plot=False
)
# now u have not only model.report but model.report_25 and so on
# plot reports
names = [name for name, _ in model.checked_reports[::-1]]
plot_several_lines(
lines=[getattr(model, name) for name in names],
colors=('green', 'black', 'red', 'blue'),
labels=['median value', '25% quantile', 'mean of population', 'best pop score'],
linewidths=(1, 1.5, 1, 2),
title="Several custom reports with base reports",
save_as='./output/report.png'
)

As u see, u should append tuple (name of report, func to evaluate report) to model.checked_report. It's highly recommended to start this name with report_ (e. g. report_my_median). And the function u use will get 1D-numpy sorted array of population scores.
There is an amazing way to control optimization process using MiddleCallbacks class. Just learn next logic:
MiddleCallbacks callbacks as list at middle_callbacks parameter in run() methodaction and condition functionscondition(data) (Callable[[MiddleCallbackData], bool]) function gets data object (dataclass MiddleCallbackData from version 6.5.0) about primary model parameters and makes logical decision about applying action functionaction(data) (Callable[[MiddleCallbackData],MiddleCallbackData]) function modifies data objects as u need -- and model will be modified by new datadata object is the structure with several parameters u can modify:
data = MiddleCallbackData(
last_generation=Generation.from_pop_matrix(pop),
current_generation=t,
report_list=self.report,
mutation_prob=self.prob_mut,
crossover_prob=self.prob_cross,
mutation=self.real_mutation,
crossover=self.crossover,
selection=self.selection,
current_stagnation=counter,
max_stagnation=self.max_stagnations,
parents_portion=self.param.parents_portion,
elit_ratio=self.param.elit_ratio,
set_function=self.set_function
)
action function gets data objects and returns data object.It's very simple to create your own action and condition functions. But there are several popular functions contained in Actions and ActionConditions classes:
actions:
Stop() -- just stop optimization processReduceMutationProb(reduce_coef = 0.9) -- reduce mutation probabilityChangeRandomCrossover(available_crossovers: Sequence[Callable[[np.ndarray, np.ndarray], Tuple[np.ndarray, np.ndarray]]]) -- change another (random) crossover from list of crossoversChangeRandomSelection(available_selections: Sequence[Callable[[np.ndarray, int], np.ndarray]])ChangeRandomMutation(available_mutations: Sequence[Callable[[float, float, float], float]])RemoveDuplicates(oppositor = None, creator = None, converter = None); see docCopyBest(by_indexes) -- copies best population object values (from dimensions in by_indexes) to all populationPlotPopulationScores(title_pattern = lambda data: f"Generation {data['current_generation']}", save_as_name_pattern = None) -- plot population scores; needs 2 functions like data->string for title and file name (to save)conditions:
ActionConditions.EachGen(generation_step = 10) -- do action each generation_step generationsActionConditions.Always() do action each generations, equals to ActionConditions.EachGen(1)ActionConditions.AfterStagnation(stagnation_generations = 50) -- do action after stagnation_generations stagnation generationsActionConditions.Several(list_of_conditions) -- do action if all conditions in list are trueTo combine action and condition to callback, just use MiddleCallbacks.UniversalCallback(action, condition) methods.
There are also next high-level useful callbacks:
MiddleCallbacks.ReduceMutationGen(reduce_coef = 0.9, min_mutation = 0.005, reduce_each_generation = 50, reload_each_generation = 500)MiddleCallbacks.GeneDiversityStats(step_generations_for_plotting:int = 10) -- plots some duplicates statistics each gen (example)

See code example
To compare efficiency of several versions of GA optimization (such as several values of several hyperparameters or including/excepting some actions like oppositions) u should make some count of simulations and compare results using some statistical test. I have realized this logic here
geneticalgorithm package)In general the performance of a genetic algorithm or any evolutionary algorithm depends on its parameters. Parameter setting of an evolutionary algorithm is important. Usually these parameters are adjusted based on experience and by conducting a sensitivity analysis. It is impossible to provide a general guideline to parameter setting but the suggestions provided below may help:
Number of iterations: Select a max_num_iterations sufficiently large; otherwise the reported solution may not be satisfactory. On the other hand
selecting a very large number of iterations increases the run time significantly. So this is actually a compromise between
the accuracy you want and the time and computational cost you spend.
Population size: Given a constant number of functional evaluations (max_num_iterations times population_size) I would select smaller population size and greater iterations. However, a very small choice of population size is also deteriorative. For most problems I would select a population size of 100 unless the dimension of the problem is very large that needs a bigger population size.
elit_ratio: Although having few elites is usually a good idea and may increase the rate of convergence in some problems, having too many elites in the population may cause the algorithm to easily trap in a local optima. I would usually select only one elite in most cases. Elitism is not always necessary and in some problems may even be deteriorative.
mutation_probability: This is a parameter you may need to adjust more than the other ones. Its appropriate value heavily depends on the problem. Sometimes we may select mutation_probability as small as 0.01 (i.e. 1 percent) and sometimes even as large as 0.5 (i.e. 50 percent) or even larger. In general if the genetic algorithm trapped in a local optimum increasing the mutation probability may help. On the other hand if the algorithm suffers from stagnation reducing the mutation probability may be effective. However, this rule of thumb is not always true.
parents_portion: If parents_portion set zero, it means that the whole of the population is filled with the newly generated solutions. On the other hand having this parameter equals 1 (i.e. 100 percent) means no new solution is generated and the algorithm would just repeat the previous values without any change which is not meaningful and effective obviously. Anything between these two may work. The exact value depends on the problem.
crossover_type: Depends on the problem. I would usually use uniform crossover. But testing the other ones in your problem is recommended.
max_iteration_without_improv: This is a parameter that I recommend being used cautiously. If this parameter is too small then the algorithm may stop while it trapped in a local optimum. So make sure you select a sufficiently large criteria to provide enough time for the algorithm to progress and to avoid immature convergence.
Finally to make sure that the parameter setting is fine, we usually should run the algorithm for several times and if convergence curves of all runs converged to the same objective function value we may accept that solution as the optimum. The number of runs depends but usually five or ten runs is prevalent. Notice that in some problems several possible set of variables produces the same objective function value. When we study the convergence of a genetic algorithm we compare the objective function values not the decision variables.
result = model.run(
no_plot = True,
)
result = model.run(
progress_bar_stream = None,
)
Try to speed up your optimizing function using Numpy, Numba or Cython. If u can, write your own set_function (function which applies to whole population samples matrix) with cython optimizations, parallelism and so.
mutation, crossover, selectionWrite faster implementations for model methods mut, mut_middle, crossover, selection and set them before running optimization process:
model.mut = custom_mut
model.crossover = custom_crossover
model.run(...)
fill_children methodFrom version 6.8.4 there is fill_children model method:
self.fill_children: Optional[Callable[[array2D, int], None]] = None
It is empty and does nothing; but if u specify it, u can get huge speed up at very intensive algorithm part. Take a look at main algo structure. There is a part with creating children from parents, this part is the most intensive because it uses python loops, calls sampling, crossover and mutations at each iteration. Using fill_children, u can rewrite this logic in your manner to speed up.
Suppose u have new population matrix pop (type np.float64, shape (population_size, dim_count)) where first parents_count rows are selected parents, next rows are filled by random, so inside fill_children method u should fill last population_size - parents_count rows (children) by using some your logic. Expected (but not mandatory) logic like this:
for k in range(self.parents_count, self.population_size, 2):
r1, r2 = get_parents_inds() # get 2 random parents indexes from [0, parents_count)
pvar1 = pop[r1]
pvar2 = pop[r2]
ch1, ch2 = self.crossover(pvar1, pvar2) # crossover
# mutations
ch1 = self.mut(ch1)
ch2 = self.mut_middle(ch2, pvar1, pvar2)
# put to population
pop[k] = ch1
pop[k+1] = ch2
Example. In one task I use this algorithm many times (100 000 generations total), so the speed matters. Every sample item is the index of element in other array there, so ith sample element is always integer value from cut [0, end[i]]. I use uniform crossover and uniform mutation (work perfect for this task). So I specified creating children logic for this task using cython.
Content of file fill_children.pyx:
#!python
#cython: language_level=3
import numpy as np
cimport numpy as np
np.import_array()
cimport cython
import math
import random
@cython.boundscheck(False)
@cython.wraparound(False)
def fill_children(
np.ndarray[np.float64_t, ndim=2] pop, # samples are integers but always float64 type
int parents_count, # count of already done parents
float mut_prob, # mutation probability
np.ndarray[np.uint8_t, ndim=1] ends # max elements for each dimension (min elements are 0)
):
cdef:
Py_ssize_t i, k, population_size = pop.shape[0], dim_count = pop.shape[1], r1, r2
float v1, v2, tmp
np.ndarray[np.float64_t, ndim=1] cross, mut, mut_middle
# making 2 children at each iteration
for k in range(parents_count, population_size, 2): # C loop, not Python
#
# 2 random parents (fast implementation)
#
r1 = random.randrange(parents_count)
r2 = random.randrange(parents_count)
if r1 == r2:
while r1 == r2: # C loop!
r2 = random.randrange(parents_count)
#
# I always need these 3 random probs sequences, so the fastest way to obtain them is np.random.random
#
cross = np.random.random(dim_count) # crossover probabilities for each dimension
mut = np.random.random(dim_count)
mut_middle = np.random.random(dim_count)
for i in range(dim_count): # C loop for each dimension
v1 = pop[r1, i] # first parent value
v2 = pop[r2, i] # second parent value
if cross[i] < 0.5: # random swap (uniform crossover), copy otherwise
tmp = v2
v2 = v1
v1 = tmp
if mut[i] < mut_prob: # random mutation for first child
# fastest way to get random integer from [0, ends[i]]
# random.random() calls not always but only on mut[i] < mut_prob
v1 = math.floor(random.random() * (ends[i] + 1))
if mut_middle[i] < mut_prob: # mut_middle for second
tmp = random.random()
if v1 < v2:
v2 = v1 + math.floor(tmp * (v2 - v1 + 1)) # integer from [v1, v2], v1 < v2
elif v1 > v2:
v2 = v2 + math.floor(tmp * (v1 - v2 + 1)) # integer from [v2, v1], v2 < v1
else:
v2 = math.floor(tmp * (ends[i] + 1))
#
# put values to children in array
#
pop[k, i] = v1
pop[k + 1, i] = v2
After compilation this file I can call it from python file to use inside GA:
mut_prob = param['mutation_probability']
def fill_children(pop: array2D, parents_count: int):
"""wrapper on fill_children.fill_children with putting local variables mut_prob, ends"""
return fill_children.fill_children(
pop, parents_count, mut_prob, ends
)
model.fill_children = fill_children
model.run(...)
Here there is the implementation of geneticalgorithm2 for some benchmark problems. Test functions are got from my OptimizationTestFunctions package.
The code for optimizations process is same for each function and is contained in file.






































See example of using GA optimization with keras neural networks for solving OpenGym tasks.
Better example is OpenGym using cost2fitness and geneticalgorithm2 where I use also my cost2fitness package for fast forward propagation
Links:
Just use no_plot = True param in run method:
model.run(no_plot = True)
If u want, u can plot results later by using
model.plot_results()
Also u can create your pretty plots using model.report object (it's a list of values):
re = np.array(model.report)
plt.plot(re)
plt.xlabel('Iteration')
plt.ylabel('Objective function')
plt.title('Genetic Algorithm')
plt.show()
There are 2 ways to plot of scores of population:
plot_pop_scores(scores, title = 'Population scores', save_as = None) function from geneticalgorithm2 environmentplot_generation_scores(self, title = 'Last generation scores', save_as = None) method of ga object for plotting scores of last generation (yes, it's wrapper of previous function)Let's check example:
import numpy as np
from geneticalgorithm2 import GeneticAlgorithm2 as ga
from geneticalgorithm2 import plot_pop_scores # for plotting scores without ga object
def f(X):
return 50 * np.sum(X) - np.sum(np.sqrt(X) * np.sin(X))
dim = 25
varbound = [[0, 10]] * dim
# create start population
start_pop = np.random.uniform(0, 10, (50, dim))
# eval scores of start population
start_scores = np.array([f(start_pop[i]) for i in range(start_pop.shape[0])])
# plot start scores using plot_pop_scores function
plot_pop_scores(start_scores, title='Population scores before beginning of searching', save_as='plot_scores_start.png')
model = ga(function=f, dimension=dim, variable_type='real', variable_boundaries=varbound)
# run optimization process
model.run(no_plot=True,
start_generation={
'variables': start_pop,
'scores': start_scores
})
# plot and save optimization process plot
model.plot_results(save_as='plot_scores_process.png')
# plot scores of last population
model.plot_generation_scores(title='Population scores after ending of searching', save_as='plot_scores_end.png')



U can do it using set_function parameter into run() method.
This function should get numpy 2D-array (samples x dimension) and return 1D-array with results.
By default it uses set_function = geneticalgorithm2.default_set_function(function), where
def default_set_function(function_for_set):
def func(matrix):
return np.array([function_for_set(matrix[i,:]) for i in range(matrix.shape[0])])
return func
U may want to use it for creating some specific or fast-vectorized evaluations like here:
def sigmoid(z):
return 1/(1+np.exp(-z))
matrix = np.random.random((1000,100))
def vectorised(X):
return sigmoid(matrix.dot(X))
model.run(set_function = vectorised)
By using set_function u can determine your own behavior for parallelism or u can use geneticalgorithm2.set_function_multiprocess(f, n_jobs = -1) for using just parallelism (recommended for heavy functions and big populations, not recommended for fast functions and small populations).
For example:
import numpy as np
from geneticalgorithm2 import GeneticAlgorithm2 as ga
def f(X):
import math
a = X[0]
b = X[1]
c = X[2]
s = 0
for i in range(10000):
s += math.sin(a * i) + math.sin(b * i) + math.cos(c * i)
return s
algorithm_param = {'max_num_iteration': 50,
'population_size': 100,
'mutation_probability': 0.1,
'elit_ratio': 0.01,
'parents_portion': 0.3,
'crossover_type': 'uniform',
'mutation_type': 'uniform_by_center',
'selection_type': 'roulette',
'max_iteration_without_improv': None}
varbound = np.array([[-10, 10]] * 3)
model = ga(function=f, dimension=3,
variable_type='real',
variable_boundaries=varbound,
algorithm_parameters=algorithm_param)
########
%time
model.run()
# Wall time: 1min 52s
%time
model.run(set_function=ga.set_function_multiprocess(f, n_jobs=6))
# Wall time: 31.7 s
For this there is start_generation parameter in run() method. It's the dictionary with structure like returned model.output_dict['last_generation']. Let's see example how can u to use it:
import numpy as np
from geneticalgorithm2 import GeneticAlgorithm2 as ga
def f(X):
return np.sum(X)
dim = 6
varbound = [(0, 10)] * dim
algorithm_param = {'max_num_iteration': 500,
'population_size': 100,
'mutation_probability': 0.1,
'elit_ratio': 0.01,
'parents_portion': 0.3,
'crossover_type': 'uniform',
'max_iteration_without_improv': None}
model = ga(function=f,
dimension=dim,
variable_type='real',
variable_boundaries=varbound,
algorithm_parameters=algorithm_param)
# start generation
# as u see u can use any values been valid for ur function
samples = np.random.uniform(0, 50, (300, dim)) # 300 is the new size of your generation
model.run(no_plot=False, start_generation={'variables': samples, 'scores': None})
# it's not necessary to evaluate scores before
# but u can do it if u have evaluated scores and don't wanna repeat calculations
# from version 6.3.0 it's recommended to use this form
from geneticalgorithm2 import Generation
model.run(no_plot=False, start_generation=Generation(variables=samples, scores=None))
# from version 6.4.0 u also can use these forms
model.run(no_plot=False, start_generation=samples)
model.run(no_plot=False, start_generation=(samples, None))
# if u have scores array, u can put it too
scores = np.array([f(sample) for sample in samples])
model.run(no_plot=False, start_generation=(samples, scores))
##
## after first run
## best value = 0.10426190111045064
##
# okay, let's continue optimization using saved last generation
model.run(no_plot=True, start_generation=model.output_dict['last_generation'])
##
## after second run
## best value = 0.06128462776296528
##
Also u can save and load populations using likely code:
import numpy as np
from geneticalgorithm2 import GeneticAlgorithm2 as ga
from OptimizationTestFunctions import Eggholder
dim = 2 * 15
f = Eggholder(dim)
xmin, xmax, ymin, ymax = f.bounds
varbound = np.array([[xmin, xmax], [ymin, ymax]] * 15)
model = ga(function=f,
dimension=dim,
variable_type='real',
variable_boundaries=varbound,
algorithm_parameters={
'max_num_iteration': 300,
'population_size': 100
})
# first run and save last generation to file
filename = "eggholder_lastgen.npz"
model.run(save_last_generation_as=filename)
# load start generation from file and run again (continue optimization)
model.run(start_generation=filename)
FAQs
Supported highly optimized and flexible genetic algorithm package for python
We found that geneticalgorithm2 demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Product
Socket’s new Tier 1 Reachability filters out up to 80% of irrelevant CVEs, so security teams can focus on the vulnerabilities that matter.
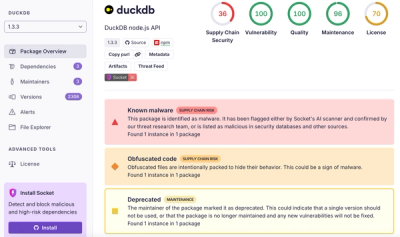
Research
/Security News
Ongoing npm supply chain attack spreads to DuckDB: multiple packages compromised with the same wallet-drainer malware.

Security News
The MCP Steering Committee has launched the official MCP Registry in preview, a central hub for discovering and publishing MCP servers.