
Security News
Research
Data Theft Repackaged: A Case Study in Malicious Wrapper Packages on npm
The Socket Research Team breaks down a malicious wrapper package that uses obfuscation to harvest credentials and exfiltrate sensitive data.
Vagabond is a comprehensive library for pathfinding, navigation, and environmental understanding in robotics and automation. It provides a range of algorithms and tools to help developers create efficient and sophisticated pathfinding solutions for robots and autonomous systems.
Vagabond is a powerful and flexible Python library designed to simplify the implementation of various pathfinding algorithms and related operations developed by Ranit Bhowmick & Sayanti Chatterjee. Whether you're working on robotics, AI, or game development, Vagabond offers an easy-to-use interface for complex algorithms like A*, Dijkstra's, and more.
To install the Vagabond library, simply use pip:
pip install py-vagabond
Here's a quick overview of how to use the library to perform A* pathfinding:
import numpy as np
import matplotlib.pyplot as plt
from vagabond.systems import node
from vagabond.environmental import astar
import numpy as np
#example free space grids (1 is free, 0 is occupied)
free_space_grid = np.array([
[1, 0.8, 0.5, 0.5, 0.8],
[0.9, 0, 0, 0.8, 0.6],
[0, 0.8, 0.9, 0.9, 0.9],
[0.8, 0.9, 0, 0, 0.9],
[0.6, 0.5, 0.2, 0.2, 1]
])
# Assuming robot_cell is defined
robot_cell = (0, 0)
end_cell = (4, 4)
start_node = node(value=robot_cell, name="({}, {})".format(robot_cell[0], robot_cell[1]))
end_node = node(value=end_cell, name="({}, {})".format(end_cell[0], end_cell[1]))
# Generate a random end cell
map_height, map_width = free_space_grid.shape
#! A* functions ----------------------------------------------------
# if a cell is given, return the 4-connected neighbors
# probability high -----> cost low -----> high priority
def get_neighbors(parent_node):
neighbors = []
x, y = parent_node.value
# Check if the neighbor is within the map and is free
if x > 0 and free_space_grid[x - 1,y] != 0:
neighbors.append(node(value=(x - 1, y), parent=parent_node, cost=(cost(parent_node, (x - 1, y)))+heuristic((x - 1, y), end_cell), name="({}, {})".format(x - 1, y)))
if x < map_width - 1 and free_space_grid[x + 1,y] != 0:
neighbors.append(node(value=(x + 1, y), parent=parent_node, cost=(cost(parent_node, (x + 1, y)))+heuristic((x + 1, y), end_cell), name="({}, {})".format(x + 1, y)))
if y > 0 and free_space_grid[x, y - 1] != 0:
neighbors.append(node(value=(x, y - 1), parent=parent_node, cost=(cost(parent_node, (x, y - 1)))+heuristic((x, y - 1), end_cell), name="({}, {})".format(x, y - 1)))
if y < map_height - 1 and free_space_grid[x, y + 1] != 0:
neighbors.append(node(value=(x, y + 1), parent=parent_node, cost=(cost(parent_node, (x, y + 1)))+heuristic((x, y + 1), end_cell), name="({}, {})".format(x, y + 1)))
return neighbors
def cost(current_cell, neighbor):
if(current_cell.parent):
parent = current_cell.parent.value
else:
parent = current_cell.value
current = current_cell.value
#check if direction has not changed
direction1 = (parent[0] - current[0], parent[1] - current[1])
direction2 = (current[0] - neighbor[0], current[1] - neighbor[1])
if direction1 == direction2:
penalty = 0.1
else:
penalty = 0.5
return penalty + round(1 - free_space_grid[neighbor],2)
def heuristic(current_cell, end_cell):
return abs(current_cell[0] - end_cell[0]) + abs(current_cell[1] - end_cell[1])
#! A* algorithm ----------------------------------------------------
# Create an instance of the astar class
astar_obj = astar(get_neighbors)
# Find the path
path = astar_obj.path(start_node, end_node)
astar_obj.display_path(filename="astar_path")
print("Path: ", path)
#! Plot the path ----------------------------------------------------
plt.figure()
plt.imshow(free_space_grid, cmap='gray', origin='upper')
# Plot the path as a line
path = np.array(astar_obj.get_raw())
#plot simplified dots
plt.plot(path[:, 1], path[:, 0], 'r')
plt.scatter(robot_cell[1], robot_cell[0], color='r', marker='x')
plt.scatter(end_cell[1], end_cell[0], color='g', marker='x')
plt.show()
This example initializes a simple 5x5 grid with varying cost values and calculates the optimal path from the top-left corner to the bottom-right corner using the A* algorithm.
The node class is the fundamental building block of the Vagabond library. It represents each cell in your grid and contains attributes like value, parent, childs, cost, and name.
Initialization:
from vagabond.systems import node
n = node(value=(x, y), parent=None, cost=0.0, name="Node (x, y)")
Attributes:
The astar class implements the A* pathfinding algorithm, which is one of the most popular algorithms used in robotics and game development due to its efficiency and accuracy.
Initialization:
from vagabond.environmental import astar
astar_obj = astar(get_neighbors)
Key Functions:
path(start_node, end_node): Calculates the optimal path between the start and end nodes.display_path(filename): Displays the grid, obstacles, and the computed path using Graphviz.get_raw(): Returns the raw path as a list of nodes.get(): Returns the path as a list of nodes.add(node): Adds a node to the path.remove(node): Removes a node from the path.clear(): Clears the path.Usage:
path = astar_obj.path(start_node, end_node)
raw_path = astar_obj.get_raw()
The dijkstra class implements Dijkstra's pathfinding algorithm, which is ideal for finding the shortest path in graphs with non-negative weights.
Initialization:
from vagabond.environmental import dijkstra
dijkstra_obj = dijkstra(get_neighbors)
Key Functions:
path(start_node, end_node): Identifies the shortest path between two nodes using Dijkstra's algorithm.display_path(filename): Displays the grid, obstacles, and the computed path using Graphviz.get_raw(): Returns the raw path as a list of nodes.get(): Returns the path as a list of nodes.add(node): Adds a node to the path.remove(node): Removes a node from the path.clear(): Clears the path.Usage:
path = dijkstra_obj.path(start_node, end_node)
raw_path = dijkstra_obj.get_raw()
The bfs class implements the Breadth-First Search algorithm, which is useful for exploring all possible paths in a graph.
Initialization:
from vagabond.environmental import bfs
bfs_obj = bfs(get_neighbors)
Key Functions:
path(start_node, end_node): Finds the shortest path between two nodes using BFS.display_path(filename): Displays the grid, obstacles, and the computed path using Graphviz.get_raw(): Returns the raw path as a list of nodes.get(): Returns the path as a list of nodes.add(node): Adds a node to the path.remove(node): Removes a node from the path.clear(): Clears the path.Usage:
path = bfs_obj.path(start_node, end_node)
raw_path = bfs_obj.get_raw()
The dfs class implements the Depth-First Search algorithm, which is useful for exploring all possible paths in a graph.
Initialization:
from vagabond.environmental import dfs
dfs_obj = dfs(get_neighbors)
Key Functions:
path(start_node, end_node): Finds the shortest path between two nodes using DFS.display_path(filename): Displays the grid, obstacles, and the computed path using Graphviz.get_raw(): Returns the raw path as a list of nodes.get(): Returns the path as a list of nodes.add(node): Adds a node to the path.remove(node): Removes a node from the path.clear(): Clears the path.Usage:
path = dfs_obj.path(start_node, end_node)
raw_path = dfs_obj.get_raw()
Vagabond provides a convenient way to visualize your grid, obstacles, and computed paths using the Graphviz library.
Display Path:
astar_obj.display_path(filename="astar_path")
This function generates a visualization of the grid, obstacles, and the computed path using Graphviz. The resulting image is saved as a PNG file with the specified filename.

It is also possible to display the grid and path using matplotlib:
plt.figure()
plt.imshow(free_space_grid, cmap='gray', origin='upper')
# Plot the path as a line
path = np.array(astar_obj.get_raw())
#plot the path
plt.plot(path[:, 1], path[:, 0], 'r')
plt.scatter(robot_cell[1], robot_cell[0], color='r', marker='x')
plt.scatter(end_cell[1], end_cell[0], color='g', marker='x')
plt.show()
This example demonstrates how to use the A* algorithm to find the optimal path in a grid with varying cost values.
import numpy as np
import matplotlib.pyplot as plt
from vagabond.systems import node
from vagabond.environmental import astar
import numpy as np
#example free space grids (1 is free, 0 is occupied)
free_space_grid = np.array([
[1, 0.8, 0.5, 0.5, 0.8],
[0.9, 0, 0, 0.8, 0.6],
[0, 0.8, 0.9, 0.9, 0.9],
[0.8, 0.9, 0, 0, 0.9],
[0.6, 0.5, 0.2, 0.2, 1]
])
# Assuming robot_cell is defined
robot_cell = (0, 0)
end_cell = (4, 4)
start_node = node(value=robot_cell, name="({}, {})".format(robot_cell[0], robot_cell[1]))
end_node = node(value=end_cell, name="({}, {})".format(end_cell[0], end_cell[1]))
# Generate a random end cell
map_height, map_width = free_space_grid.shape
#! A* functions ----------------------------------------------------
# if a cell is given, return the 4-connected neighbors
# probability high -----> cost low -----> high priority
def get_neighbors(parent_node):
neighbors = []
x, y = parent_node.value
# Check if the neighbor is within the map and is free
if x > 0 and free_space_grid[x - 1,y] != 0:
neighbors.append(node(value=(x - 1, y), parent=parent_node, cost=(cost(parent_node, (x - 1, y)))+heuristic((x - 1, y), end_cell), name="({}, {})".format(x - 1, y)))
if x < map_width - 1 and free_space_grid[x + 1,y] != 0:
neighbors.append(node(value=(x + 1, y), parent=parent_node, cost=(cost(parent_node, (x + 1, y)))+heuristic((x + 1, y), end_cell), name="({}, {})".format(x + 1, y)))
if y > 0 and free_space_grid[x, y - 1] != 0:
neighbors.append(node(value=(x, y - 1), parent=parent_node, cost=(cost(parent_node, (x, y - 1)))+heuristic((x, y - 1), end_cell), name="({}, {})".format(x, y - 1)))
if y < map_height - 1 and free_space_grid[x, y + 1] != 0:
neighbors.append(node(value=(x, y + 1), parent=parent_node, cost=(cost(parent_node, (x, y + 1)))+heuristic((x, y + 1), end_cell), name="({}, {})".format(x, y + 1)))
return neighbors
def cost(current_cell, neighbor):
if(current_cell.parent):
parent = current_cell.parent.value
else:
parent = current_cell.value
current = current_cell.value
#check if direction has not changed
direction1 = (parent[0] - current[0], parent[1] - current[1])
direction2 = (current[0] - neighbor[0], current[1] - neighbor[1])
if direction1 == direction2:
penalty = 0.1
else:
penalty = 0.5
return penalty + round(1 - free_space_grid[neighbor],2)
def heuristic(current_cell, end_cell):
return abs(current_cell[0] - end_cell[0]) + abs(current_cell[1] - end_cell[1])
#! A* algorithm ----------------------------------------------------
# Create an instance of the astar class
astar_obj = astar(get_neighbors)
# Find the path
path = astar_obj.path(start_node, end_node)
astar_obj.display_path(filename="astar_path")
print("Path: ", path)
#! Plot the path ----------------------------------------------------
plt.figure()
plt.imshow(free_space_grid, cmap='gray', origin='upper')
# Plot the path as a line
path = np.array(astar_obj.get_raw())
plt.plot(path[:, 1], path[:, 0], 'r')
plt.scatter(robot_cell[1], robot_cell[0], color='r', marker='x')
plt.scatter(end_cell[1], end_cell[0], color='g', marker='x')
plt.show()
This example demonstrates how to use Dijkstra's algorithm to find the shortest path in a grid with varying cost values.
import numpy as np
import matplotlib.pyplot as plt
from vagabond.systems import node
from vagabond.environmental import dijkstra
import numpy as np
#example free space grids (1 is free, 0 is occupied)
free_space_grid = np.array([
[1, 0.8, 0.5, 0.5, 0.8],
[0.9, 0, 0, 0.8, 0.6],
[0, 0.8, 0.9, 0.9, 0.9],
[0.8, 0.9, 0, 0, 0.9],
[0.6, 0.5, 0.2, 0.2, 1]
])
# Assuming robot_cell is defined
robot_cell = (0, 0)
end_cell = (4, 4)
start_node = node(value=robot_cell, name="({}, {})".format(robot_cell[0], robot_cell[1]))
end_node = node(value=end_cell, name="({}, {})".format(end_cell[0], end_cell[1]))
# Generate a random end cell
map_height, map_width = free_space_grid.shape
#! A* functions ----------------------------------------------------
# if a cell is given, return the 4-connected neighbors
# probability high -----> cost low -----> high priority
def get_neighbors(parent_node):
neighbors = []
x, y = parent_node.value
# Check if the neighbor is within the map and is free
if x > 0 and free_space_grid[x - 1,y] != 0:
neighbors.append(node(value=(x - 1, y), parent=parent_node, cost=(cost(parent_node, (x - 1, y)))+heuristic((x - 1, y), end_cell), name="({}, {})".format(x - 1, y)))
if x < map_width - 1 and free_space_grid[x + 1,y] != 0:
neighbors.append(node(value=(x + 1, y), parent=parent_node, cost=(cost(parent_node, (x + 1, y)))+heuristic((x + 1, y), end_cell), name="({}, {})".format(x + 1, y)))
if y > 0 and free_space_grid[x, y - 1] != 0:
neighbors.append(node(value=(x, y - 1), parent=parent_node, cost=(cost(parent_node, (x, y - 1)))+heuristic((x, y - 1), end_cell), name="({}, {})".format(x, y - 1)))
if y < map_height - 1 and free_space_grid[x, y + 1] != 0:
neighbors.append(node(value=(x, y + 1), parent=parent_node, cost=(cost(parent_node, (x, y + 1)))+heuristic((x, y + 1), end_cell), name="({}, {})".format(x, y + 1)))
return neighbors
def cost(current_cell, neighbor):
if(current_cell.parent):
parent = current_cell.parent.value
else:
parent = current_cell.value
current = current_cell.value
#check if direction has not changed
direction1 = (parent[0] - current[0], parent[1] - current[1])
direction2 = (current[0] - neighbor[0], current[1] - neighbor[1])
if direction1 == direction2:
penalty = 0.1
else:
penalty = 0.5
return penalty + round(1 - free_space_grid[neighbor],2)
def heuristic(current_cell, end_cell):
return abs(current_cell[0] - end_cell[0]) + abs(current_cell[1] - end_cell[1])
#! A* algorithm ----------------------------------------------------
# Create an instance of the astar class
dijkstra_obj = dijkstra(get_neighbors)
# Find the path
path = dijkstra_obj.path(start_node, end_node)
dijkstra_obj.display_path(filename="dijkstra_path")
print("Path: ", path)
#! Plot the path ----------------------------------------------------
plt.figure()
plt.imshow(free_space_grid, cmap='gray', origin='upper')
# Plot the path as a line
path = np.array(dijkstra_obj.get_raw())
#plot simplified dots
plt.plot(path[:, 1], path[:, 0], 'r')
plt.scatter(robot_cell[1], robot_cell[0], color='r', marker='x')
plt.scatter(end_cell[1], end_cell[0], color='g', marker='x')
plt.show()
This example demonstrates how to use the Breadth-First Search algorithm to explore all possible paths in a grid.
import numpy as np
import matplotlib.pyplot as plt
from vagabond.systems import node
from vagabond.environmental import bfs
import numpy as np
#example free space grids (1 is free, 0 is occupied)
free_space_grid = np.array([
[1, 0.8, 0.5, 0.5, 0.8],
[0.9, 0, 0, 0.8, 0.6],
[0, 0.8, 0.9, 0.9, 0.9],
[0.8, 0.9, 0, 0, 0.9],
[0.6, 0.5, 0.2, 0.2, 1]
])
# Assuming robot_cell is defined
robot_cell = (0, 0)
end_cell = (4, 4)
start_node = node(value=robot_cell, name="({}, {})".format(robot_cell[0], robot_cell[1]))
end_node = node(value=end_cell, name="({}, {})".format(end_cell[0], end_cell[1]))
# Generate a random end cell
map_height, map_width = free_space_grid.shape
#! A* functions ----------------------------------------------------
# if a cell is given, return the 4-connected neighbors
# probability high -----> cost low -----> high priority
def get_neighbors(parent_node):
neighbors = []
x, y = parent_node.value
# Check if the neighbor is within the map and is free
if x > 0 and free_space_grid[x - 1,y] != 0:
neighbors.append(node(value=(x - 1, y), parent=parent_node, cost=(cost(parent_node, (x - 1, y)))+heuristic((x - 1, y), end_cell), name="({}, {})".format(x - 1, y)))
if x < map_width - 1 and free_space_grid[x + 1,y] != 0:
neighbors.append(node(value=(x + 1, y), parent=parent_node, cost=(cost(parent_node, (x + 1, y)))+heuristic((x + 1, y), end_cell), name="({}, {})".format(x + 1, y)))
if y > 0 and free_space_grid[x, y - 1] != 0:
neighbors.append(node(value=(x, y - 1), parent=parent_node, cost=(cost(parent_node, (x, y - 1)))+heuristic((x, y - 1), end_cell), name="({}, {})".format(x, y - 1)))
if y < map_height - 1 and free_space_grid[x, y + 1] != 0:
neighbors.append(node(value=(x, y + 1), parent=parent_node, cost=(cost(parent_node, (x, y + 1)))+heuristic((x, y + 1), end_cell), name="({}, {})".format(x, y + 1)))
return neighbors
def cost(current_cell, neighbor):
if(current_cell.parent):
parent = current_cell.parent.value
else:
parent = current_cell.value
current = current_cell.value
#check if direction has not changed
direction1 = (parent[0] - current[0], parent[1] - current[1])
direction2 = (current[0] - neighbor[0], current[1] - neighbor[1])
if direction1 == direction2:
penalty = 0.1
else:
penalty = 0.5
return penalty + round(1 - free_space_grid[neighbor],2)
def heuristic(current_cell, end_cell):
return abs(current_cell[0] - end_cell[0]) + abs(current_cell[1] - end_cell[1])
#! A* algorithm ----------------------------------------------------
# Create an instance of the astar class
bfs_obj = bfs(get_neighbors)
# Find the path
path = bfs_obj.path(start_node, end_node)
bfs_obj.display_path(filename="bfs_path")
print("Path: ", path)
#! Plot the path ----------------------------------------------------
plt.figure()
plt.imshow(free_space_grid, cmap='gray', origin='upper')
# Plot the path as a line
path = np.array(bfs_obj.get_raw())
#plot simplified dots
plt.plot(path[:, 1], path[:, 0], 'r')
plt.scatter(robot_cell[1], robot_cell[0], color='r', marker='x')
plt.scatter(end_cell[1], end_cell[0], color='g', marker='x')
plt.show()
This example demonstrates how to use the Depth-First Search algorithm to explore all possible paths in a grid.
import numpy as np
import matplotlib.pyplot as plt
from vagabond.systems import node
from vagabond.environmental import dfs
import numpy as np
#example free space grids (1 is free, 0 is occupied)
free_space_grid = np.array([
[1, 0.8, 0.5, 0.5, 0.8],
[0.9, 0, 0, 0.8, 0.6],
[0, 0.8, 0.9, 0.9, 0.9],
[0.8, 0.9, 0, 0, 0.9],
[0.6, 0.5, 0.2, 0.2, 1]
])
# Assuming robot_cell is defined
robot_cell = (0, 0)
end_cell = (4, 4)
start_node = node(value=robot_cell, name="({}, {})".format(robot_cell[0], robot_cell[1]))
end_node = node(value=end_cell, name="({}, {})".format(end_cell[0], end_cell[1]))
# Generate a random end cell
map_height, map_width = free_space_grid.shape
#! A* functions ----------------------------------------------------
# if a cell is given, return the 4-connected neighbors
# probability high -----> cost low -----> high priority
def get_neighbors(parent_node):
neighbors = []
x, y = parent_node.value
# Check if the neighbor is within the map and is free
if x > 0 and free_space_grid[x - 1,y] != 0:
neighbors.append(node(value=(x - 1, y), parent=parent_node, cost=(cost(parent_node, (x - 1, y)))+heuristic((x - 1, y), end_cell), name="({}, {})".format(x - 1, y)))
if x < map_width - 1 and free_space_grid[x + 1,y] != 0:
neighbors.append(node(value=(x + 1, y), parent=parent_node, cost=(cost(parent_node, (x + 1, y)))+heuristic((x + 1, y), end_cell), name="({}, {})".format(x + 1, y)))
if y > 0 and free_space_grid[x, y - 1] != 0:
neighbors.append(node(value=(x, y - 1), parent=parent_node, cost=(cost(parent_node, (x, y - 1)))+heuristic((x, y - 1), end_cell), name="({}, {})".format(x, y - 1)))
if y < map_height - 1 and free_space_grid[x, y + 1] != 0:
neighbors.append(node(value=(x, y + 1), parent=parent_node, cost=(cost(parent_node, (x, y + 1)))+heuristic((x, y + 1), end_cell), name="({}, {})".format(x, y + 1)))
return neighbors
def cost(current_cell, neighbor):
if(current_cell.parent):
parent = current_cell.parent.value
else:
parent = current_cell.value
current = current_cell.value
#check if direction has not changed
direction1 = (parent[0] - current[0], parent[1] - current[1])
direction2 = (current[0] - neighbor[0], current[1] - neighbor[1])
if direction1 == direction2:
penalty = 0.1
else:
penalty = 0.5
return penalty + round(1 - free_space_grid[neighbor],2)
def heuristic(current_cell, end_cell):
return abs(current_cell[0] - end_cell[0]) + abs(current_cell[1] - end_cell[1])
#! A* algorithm ----------------------------------------------------
# Create an instance of the astar class
dfs_obj = dfs(get_neighbors)
# Find the path
path = dfs_obj.path(start_node, end_node)
dfs_obj.display_path(filename="dfs_path")
print("Path: ", path)
#! Plot the path ----------------------------------------------------
plt.figure()
plt.imshow(free_space_grid, cmap='gray', origin='upper')
# Plot the path as a line
path = np.array(dfs_obj.get_raw())
#plot simplified dots
plt.plot(path[:, 1], path[:, 0], 'r')
plt.scatter(robot_cell[1], robot_cell[0], color='r', marker='x')
plt.scatter(end_cell[1], end_cell[0], color='g', marker='x')
plt.show()
FAQs
Vagabond is a comprehensive library for pathfinding, navigation, and environmental understanding in robotics and automation. It provides a range of algorithms and tools to help developers create efficient and sophisticated pathfinding solutions for robots and autonomous systems.
We found that py-vagabond demonstrated a healthy version release cadence and project activity because the last version was released less than a year ago. It has 1 open source maintainer collaborating on the project.
Did you know?

Socket for GitHub automatically highlights issues in each pull request and monitors the health of all your open source dependencies. Discover the contents of your packages and block harmful activity before you install or update your dependencies.

Security News
Research
The Socket Research Team breaks down a malicious wrapper package that uses obfuscation to harvest credentials and exfiltrate sensitive data.
Research
Security News
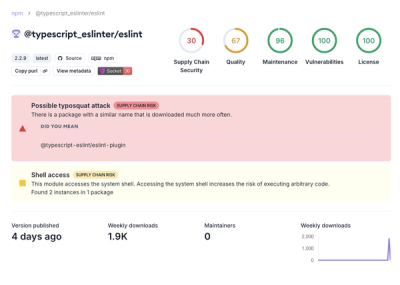
Attackers used a malicious npm package typosquatting a popular ESLint plugin to steal sensitive data, execute commands, and exploit developer systems.

Security News
The Ultralytics' PyPI Package was compromised four times in one weekend through GitHub Actions cache poisoning and failure to rotate previously compromised API tokens.